Chapter 4 General Vector Spaces Face Recognition ( á¹¢å ± 彐嬀)

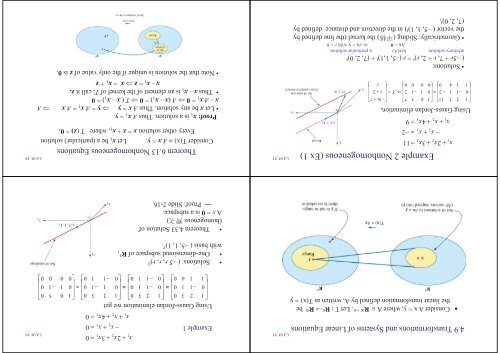
4.9 Transformations and Systems of Linear Equations Consider A x = y, where A R m n . Let T : R n R m bethe linear transformation defined by A, written as T(x) = yx1x1 2 x xExample 2 Nonhomogeneous (Ex 1)2x223xx 4 x333 11 2 9Using Gauss-Jordan elimination,1 2 30 1 11 1 411 29 1 0 5 70 1 1 20 0 0 0 5 r X r 2 r7 • Solutions:( –5r + 7, r + 2, r) t = r (–5, 1,1) t + (7, 2, 0) tarbitrary solution ker(A) a particular solutionAx = 0 to Ax = y with r = 0• Geometrically: Sliding () the kernel (the line defined bythe vector ( –5, 1, 1) t ) in the direction and distance defined by(7, 2, 0) t .LA 04_85LA 04_87x1 2 x2 3Example 1 x2x1 x2 4Using Gauss-Jordan elimination we get3 0 1 21 0 0 11 0 0 1 1 2 3 0 1 2 0 1 1 0 0 1 1 1 4 0 0 1 xxx333311000000100010510000LA 04_86• Solutions: ( –5 r, r, r) T• One-dimensional subspace of R 3 ,with basis ( –5, 1, 1) T .• Theorem 4.33 Solution of(homogenous )A x = 0 is a subspace. Proof: Slide 2-16.Theorem 6.13 Nonhomogeneous EquationsConsider T(x) A x = y. Let x 1 be a (particular) solutionEvery other solution x = z + x 1 , where T (z) = 0.LA 04_88Proof: x 1 is a solution. Thus A x 1 = y.•Let x be any solution. Thus A x = y y = A x 1 = A x Ax – A x 1 = 0 A (x – x 1 )= 0 T ( x – x 1 )= 0• Thus x – x 1 is an element of the kernel of T; call it z.x – x 1 = z x = x 1 + z• Note that the solution is unique if the only value of z is 0.