G. Besson THE GEOMETRIZATION CONJECTURE AFTER R ...

More documents

Recommendations

Info

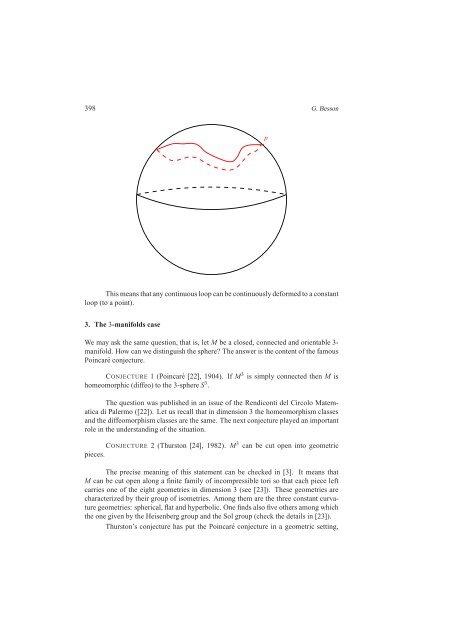
398 G. BessonpThis means that any continuous loop can be continuously deformed to a constantloop (to a point).3. The 3-manifolds caseWe may ask the same question, that is, let M be a closed, connected and orientable 3-manifold. How can we distinguish the sphere? The answer is the content of the famousPoincaré conjecture.CONJECTURE 1 (Poincaré [22], 1904). If M 3 is simply connected then M ishomeomorphic (diffeo) to the 3-sphere S 3 .The question was published in an issue of the Rendiconti del Circolo Matematicadi Palermo ([22]). Let us recall that in dimension 3 the homeomorphism classesand the diffeomorphism classes are the same. The next conjecture played an importantrole in the understanding of the situation.CONJECTURE 2 (Thurston [24], 1982). M 3 can be cut open into geometricpieces.The precise meaning of this statement can be checked in [3]. It means thatM can be cut open along a finite family of incompressible tori so that each piece leftcarries one of the eight geometries in dimension 3 (see [23]). These geometries arecharacterized by their group of isometries. Among them are the three constant curvaturegeometries: spherical, flat and hyperbolic. One finds also five others among whichthe one given by the Heisenberg group and the Sol group (check the details in [23]).Thurston’s conjecture has put the Poincaré conjecture in a geometric setting,
The Geometrization Conjecture 399namely the purely topological statement of Poincaré is understood in geometrical terms:a simply connected 3-manifold should carry a spherical geometry. Letting the geometryenter the picture opens the Pandora box; the analysis comes with the geometry.4. Some basic differential geometryThe idea developed by R. Hamilton is to deform continuously the ”shape” of a manifoldin order to let the various pieces, in Thurston’s sense, appear. What do we mean by”shape”?4.1. Shape of a differentiable manifold: the sectional curvatureBy ”shape” we mean a Riemannian metric denoted by g. Let us recall that it is a Euclideanscalar product on each tangent space, T m (M), for m ∈ M. Although the situationis infinitesimally Euclidean (i.e. on each tangent space) it is not locally. The defect tobeing locally Euclidean is given by the curvature. Giving the precise definitions, explanationsand examples would be beyond the scope of this text. The reader is referredto the standard textbooks such as [6] or [9]. The paradigm is the 2-dimensional Gaußcurvature. Let us take, for m ∈ M, a 2-plane P ⊂ T m (M).PmLet us consider the piece of surface obtained by the family of geodesics startingfrom m and tangent to a vector in P, then the sectional curvature associated to P,denoted by K(P) is the Gauß curvature at m (and only at m) of this surface.4.2. The Ricci curvatureThe most important object is the Ricci curvature which is an average of the sectionalcurvature. Let u ∈ T m (M) be a unit vector and (u,e 2 ,e 3 ) and orthonormal basis ofT m (M). Then,Ricci(u,u) = K(u,e 2 )+K(u,e 3 ).This definition is however not enlightening. Let us look at the picture below,
Page 1: Rend. Sem. Mat. Univ. Pol. Torino -
Page 5 and 6: The Geometrization Conjecture 401qu
Page 7 and 8: The Geometrization Conjecture 403Ca
Page 9 and 10: The Geometrization Conjecture 405th
Page 11 and 12: The Geometrization Conjecture 407Th
Page 13 and 14: The Geometrization Conjecture 409Zo
Page 15: The Geometrization Conjecture 411[7

G. Besson THE GEOMETRIZATION CONJECTURE AFTER R ...

Create successful ePaper yourself

Delete template?

Save as template?