C - Fen Bilimleri Enstitüsü - Erciyes Üniversitesi

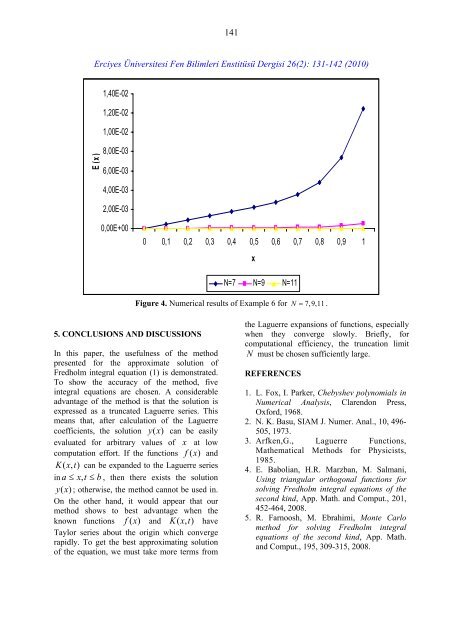
141Erciyes Üniversitesi Fen Bilimleri Enstitüsü Dergisi 26(2): 131-142 (2010)E (x )1,40E-021,20E-021,00E-028,00E-036,00E-034,00E-032,00E-030,00E+000 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1xN=7 N=9 N=11Figure 4. Numerical results of Example 6 for N = 7,9, 11 .5. CONCLUSIONS AND DISCUSSIONSIn this paper, the usefulness of the methodpresented for the approximate solution ofFredholm integral equation (1) is demonstrated.To show the accuracy of the method, fiveintegral equations are chosen. A considerableadvantage of the method is that the solution isexpressed as a truncated Laguerre series. Thismeans that, after calculation of the Laguerrecoefficients, the solution y (x)can be easilyevaluated for arbitrary values of x at lowcomputation effort. If the functions f (x)andK ( x,t)can be expanded to the Laguerre seriesin a ≤ x, t ≤ b , then there exists the solutiony (x) ; otherwise, the method cannot be used in.On the other hand, it would appear that ourmethod shows to best advantage when theknown functions f (x)and K ( x,t)haveTaylor series about the origin which convergerapidly. To get the best approximating solutionof the equation, we must take more terms fromthe Laguerre expansions of functions, especiallywhen they converge slowly. Briefly, forcomputational efficiency, the truncation limitN must be chosen sufficiently large.REFERENCES1. L. Fox, I. Parker, Chebyshev polynomials inNumerical Analysis, Clarendon Press,Oxford, 1968.2. N. K. Basu, SIAM J. Numer. Anal., 10, 496-505, 1973.3. Arfken,G., Laguerre Functions,Mathematical Methods for Physicists,1985.4. E. Babolian, H.R. Marzban, M. Salmani,Using triangular orthogonal functions forsolving Fredholm integral equations of thesecond kind, App. Math. and Comput., 201,452-464, 2008.5. R. Farnoosh, M. Ebrahimi, Monte Carlomethod for solving Fredholm integralequations of the second kind, App. Math.and Comput., 195, 309-315, 2008.