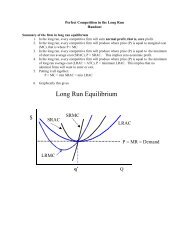
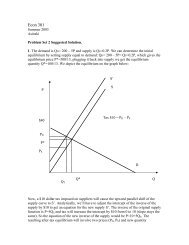
SAMPLE MOMENTS 1.1. Moments about the origin (raw moments ...

6 SAMPLE MOMENTSE ( [Mn2 ) n]1 =n E ∑Xi2 − E [ ¯X 2 ]ni=1(2= 1 n∑µ ′ 1n∑i,2 − µ ′nni,1)− Var( ¯X n )i=1= µ ′ 2 − (µ′ 1 )2 − σ2n= σ 2 − 1 n σ2= n − 1ni=1σ 2 (31)where µ ′ 1 and µ ′ 2 are the first and second population moments, and µ 2 is the second central populationmoment for the identically distributed variables. Note that this obviously implies[∑ n(E Xi − ¯X ) ]2i=1= nE ( )Mn2( ) n − 1(32)= nσ 2n=(n − 1) σ 24.2.3. Variance of M 2 n. By definition,Var ( Mn2 ) [ (M ) ]= E2 2n − ( EMn) 2 2(33)The second term on the right on equation 33 is easily obtained by squaring the result in equation 31.E ( Mn2 ) n − 1 = σ 2n⇒ ( E ( (34)))Mn2 2 ( )= EM2 2 (n − 1) 2n =n 2 σ 4Now consider the first term on the right hand side of equation 33. Write it as[ (M )2 2]E n⎡(=E ⎣1n) ⎤ 2 n∑ (Xi − ¯X) 2n⎦ (35)i =1Now consider writing 1 n∑ ni =1(Xi − ¯X n) 2as follows