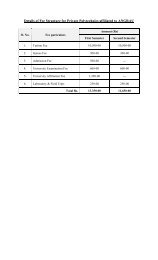
Course No Course Title Credits

(In the derivations, the expression for the derivative at
x + dx
has been
written in the form of a Taylor-Series expression with only the first two terms
of the series employed for the development.)
where
.
q = energy generated per unit volume, W /m 3
c = specific heat of material, J /kg .°C
ρ = density, kg/m 3
Combining the relations above gives
or
heat source.
∂
− kA T
+
∂x
q .
Adx =
∂T
ρcA
dx ∂τ
⎡ ∂T
− A⎢k
⎣ ∂x
.
∂ ⎛ ∂T
⎞ ∂T
⎜k
⎟dx
+ q=ρc
∂x
⎝ ∂x
⎠ ∂ τ
∂ ⎛ ∂T
⎞ ⎤
+ ⎜k
⎟dx
∂x
⎥
⎝ ∂x
⎠ ⎦
This is the one-dimensional steady state heat-conduction equation with
Figure 2.2 Elemental volume for three-dimensional heat-conduction analysis:
(a) cartesian coordinates; (b) cylindrical coordinates;
(c) spherical coordinates.