Lecture 3 Trigonometric Functions Graphs

Lecture 3: Trigonometric Functions: Graphs
3.1 The graph of the sine function
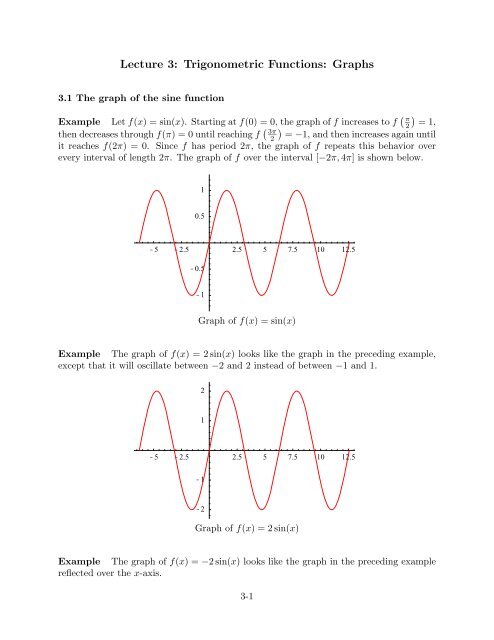
Example Let f(x) = sin(x). Starting at f(0) = 0, the graph of f increases to f ( )
π
2 = 1,
then decreases through f(π) = 0 until reaching f ( )
3π
2 = −1, and then increases again until
it reaches f(2π) = 0. Since f has period 2π, the graph of f repeats this behavior over
every interval of length 2π. The graph of f over the interval [−2π, 4π] is shown below.
1
0.5
-5 -2.5 2.5 5 7.5 10 12.5
-0.5
-1
Graph of f(x) = sin(x)
Example The graph of f(x) = 2 sin(x) looks like the graph in the preceding example,
except that it will oscillate between −2 and 2 instead of between −1 and 1.
2
1
-5 -2.5 2.5 5 7.5 10 12.5
-1
-2
Graph of f(x) = 2 sin(x)
Example The graph of f(x) = −2 sin(x) looks like the graph in the preceding example
reflected over the x-axis.
3-1

Lecture 3: Trigonometric Functions: Graphs 3-2
2
1
-5 -2.5 2.5 5 7.5 10 12.5
-1
-2
Graph of f(x) = −2 sin(x)
In both of the preceding examples, we say the function has amplitude 2.
Example The graph of f(x) = sin(2x) will look like the graph of sin(x), except that it
completes an entire oscillation over the interval [0, π]. That is, f has period π.
1
0.5
-5 -2.5 2.5 5 7.5 10 12.5
-0.5
-1
Graph of f(x) = sin(2x)
Example The graph of f(x) = sin (x − π) is the graph of sin(x) shifted horizontally to
the right by π. We call π the phase angle of f.
In general, for constants a, b, and c,
f(x) = a sin(b(x − c))
has amplitude |a|, period 2π
|b|
, and phase angle c.
Example
Let f(x) = 4 sin(2πx + π). Then
f(x) = 4 sin
(
2π
(
x + 1 ))
,
2

Lecture 3: Trigonometric Functions: Graphs 3-3
1
0.5
-5 -2.5 2.5 5 7.5 10 12.5
-0.5
-1
Graph of f(x) = sin(x − π)
4
2
-2 -1 1 2
-2
-4
Graph of f(x) = 4 sin(2 ∗ πx + π)
so f has amplitude 4, period 1, and phase angle 1 2 .
3.2 Graphs of the other trigonometric functions
Example
Note that
(
sin x + π )
( π
)
( π
)
= sin(x) cos + cos(x) sin = cos(x).
2
2 2
Hence the graph of f(x) = cos(x) is the graph of sin(x) shifted to the left by π 2 .
As above, for constants a, b, and c,
f(x) = a cos(b(x − c))
has amplitude |a|, period 2π
|b|
, and phase angle c.

Lecture 3: Trigonometric Functions: Graphs 3-4
1
0.5
-5 -2.5 2.5 5 7.5 10 12.5
-0.5
-1
Graph of f(x) = cos(x)
Example
Let f(x) = tan(x). Note that
and
lim tan(x) =
x→ π 2 −
lim tan(x) =
x→− π 2 +
lim
x→ π 2 −
lim
x→− π 2 +
sin(x)
cos(x) = ∞
sin(x)
cos(x) = −∞.
Hence the lines x = − π 2 and x = π 2
are vertical asymptotes for the graph f. Recalling
that tan(x) has period π, we can understand why the graph of f looks as it does in the
following plot.
10
7.5
5
2.5
-4 -2 2 4
-2.5
-5
-7.5
-10
Graph of f(x) = tan(x)
Example
Let f(x) = sec(x). Note that
lim sec(x) = lim 1
x→− π 2 + x→− π 2 + cos(x) = ∞,

Lecture 3: Trigonometric Functions: Graphs 3-5
and
1
lim sec(x) = lim
x→ π 2 − x→ π 2 − cos(x) = ∞,
1
lim sec(x) = lim
x→ π 2 + x→ π 2 + cos(x) = −∞,
lim sec(x) =
x→ 3π −
2
lim
x→ 3π −
2
1
cos(x) = −∞.
Hence [ the lines x = − π 2 , x = π 2 , and x = 3π 2
. Also, note that sec(x) ≥ 1 for all x in
−
π
2 , ] [ π
2 and sec(x) ≤ −1 for all x in π
2 , ] 3π
2 . Combining this information with the fact
that sec(x) has period 2π, we can understand why the graph of f looks as it does in the
following plot.
4
2
-4 -2 2 4 6 8
-2
-4
Graph of f(x) = sec(x)