The Topography of Multivariate Normal Mixtures
The Topography of Multivariate Normal Mixtures
The Topography of Multivariate Normal Mixtures
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>The</strong> <strong>Topography</strong> <strong>of</strong> <strong>Multivariate</strong><br />
<strong>Normal</strong> <strong>Mixtures</strong><br />
Post Doctoral Talk<br />
SAMSI<br />
Surajit Ray<br />
EMAIL: sray@bios.unc.edu<br />
Surajit Ray Nov 2, 2004
Mixture <strong>of</strong> Distributions<br />
■ Flexible way <strong>of</strong> modeling heterogeneous population.<br />
■ Data reduction through the number, location and shape <strong>of</strong> Mixture<br />
components.<br />
■ Can be directly used for model based clustering.<br />
Surajit Ray Nov 2, 2004
Mixture <strong>of</strong> Distributions<br />
-component mixture:<br />
¡<br />
¢¤£<br />
�<br />
�<br />
¨<br />
Parameters<br />
¨��<br />
�<br />
¥<br />
¡<br />
¢¤£<br />
¥<br />
� component densities. �<br />
�<br />
�<br />
�<br />
¨<br />
� �<br />
��<br />
��<br />
¦<br />
§ ¨�©<br />
�<br />
��<br />
����<br />
� �<br />
� ��<br />
�<br />
�<br />
�<br />
¨<br />
¡<br />
and<br />
¨<br />
¢¤£<br />
�<br />
�<br />
¨<br />
¨��<br />
�<br />
¥<br />
� mixing proportions.<br />
Surajit Ray Nov 2, 2004<br />
�<br />
�<br />
� §<br />
� §<br />
§ ¨©<br />
�<br />
�<br />
¨<br />
��� ¦
Number <strong>of</strong> components Number <strong>of</strong> Modes<br />
0.0 0.05 0.10 0.15 0.20<br />
-6 -4 -2 0 2 4 6<br />
Mixture <strong>of</strong> normals 4 standard deviations apart<br />
¡<br />
¢£<br />
0.0 0.05 0.10 0.15 0.20 0.25<br />
-6 -4 -2 0 2 4 6<br />
Mixture <strong>of</strong> normals 2 standard deviations apart<br />
Bimodal Unimodal<br />
¤ number<br />
<strong>of</strong> modes.<br />
NOTE: Practical interest could lie in finding components that correspond<br />
to separate modes.<br />
Surajit Ray Nov 2, 2004
Detection <strong>of</strong> modality: Univariate Case<br />
■ Conditions for bimodality <strong>of</strong> two univariate normals<br />
<strong>The</strong>orem 1. (?).<br />
■ Conditions for arbitrary mixture in (??)<br />
§ ¢�<br />
¦<br />
¡<br />
¤<br />
�<br />
¢£¢<br />
¢<br />
�<br />
§<br />
��<br />
¨©<br />
Surajit Ray Nov 2, 2004<br />
¤<br />
¢�<br />
¥<br />
¥<br />
¢ �<br />
¦<br />
¥<br />
© � ¦<br />
�<br />
¥<br />
¢£¢�<br />
�<br />
¤<br />
¥
Modal Structure...<strong>Topography</strong><br />
■ Modes are potentially symptomatic to the underlying population<br />
structure.<br />
Studying modal structures in high dimensions is extremely challenging.<br />
Our Goals<br />
■ Study the topography <strong>of</strong> normal mixtures in high dimension.<br />
■ Provide analytical and graphical solution for determining the number <strong>of</strong><br />
modes.<br />
■ Show how it can be used to find the number <strong>of</strong> clusters in high<br />
dimensional data � Modal Clusters.<br />
Surajit Ray Nov 2, 2004
Modality: <strong>Multivariate</strong> Distribution<br />
density<br />
0.1<br />
0.08<br />
0.06<br />
0.04<br />
0.02<br />
0<br />
4<br />
2<br />
0<br />
y<br />
−2<br />
−4<br />
−4<br />
(1,1)<br />
(−1,−1)<br />
Bivariate normal with means (-1,-1) and (1,1)<br />
Surajit Ray Nov 2, 2004<br />
−2<br />
x<br />
0<br />
2<br />
4
Modality: <strong>Multivariate</strong> Distribution<br />
density<br />
0.0 0.1 0.2 0.3 0.4 0.5<br />
−4 −2 0 2 4<br />
x−axis<br />
Marginal distribution in<br />
and£ -axis.<br />
Surajit Ray Nov 2, 2004
Modality: <strong>Multivariate</strong> Distribution<br />
z3<br />
0.00 0.05 0.10 0.15 0.20 0.25<br />
−4 −2 0 2 4<br />
Distribution along the line<br />
Surajit Ray Nov 2, 2004<br />
z1<br />
¦<br />
£
Modality: Equal variance<br />
■ A mixture <strong>of</strong> multivariate normal is bimodal<br />
distribution along some line is bimodal.<br />
■ Get the axis <strong>of</strong> maximum separation.<br />
■ Use the bimodality condition in the univariate case.<br />
<strong>The</strong>orem 2. <strong>Multivariate</strong> Modality Condition: Equal variance Case<br />
<strong>The</strong> distribution <strong>of</strong><br />
is bimodal iff<br />
¢£¢<br />
�<br />
¡<br />
¦<br />
�<br />
¢£¢<br />
¢�<br />
¥<br />
£<br />
¢¤<br />
�¢£¢<br />
��<br />
¢�<br />
¥ ¢<br />
¥<br />
¦<br />
�<br />
¥<br />
¢£¢�<br />
¡<br />
the univariate<br />
Surajit Ray Nov 2, 2004<br />
�<br />
¦<br />
¢�<br />
¥¦¥<br />
§<br />
�<br />
¢<br />
¥
Unequal variance<br />
Two components, unequal variance:<br />
<strong>The</strong> mixture density with<br />
¢£<br />
¤<br />
¥ ¦<br />
§ §<br />
¨ ©�<br />
� £<br />
¤<br />
¥ ¦<br />
�<br />
y<br />
−1 0 1 2 3<br />
§ �<br />
§��<br />
§<br />
©<br />
¦<br />
¨ ©�<br />
¢�<br />
and<br />
¤<br />
¥ ¦<br />
� �<br />
−2 −1 0 1 2<br />
¡<br />
©<br />
and �<br />
¦<br />
¨ ©�<br />
� �<br />
¥ ¦ �<br />
¤<br />
the following parameters:<br />
Surajit Ray Nov 2, 2004<br />
x<br />
�§<br />
§<br />
�<br />
§<br />
¨ ©�<br />
�<br />
�<br />
¦ � ¥<br />
¤<br />
�<br />
�<br />
�<br />
¨ ©
¢¡<br />
¥<br />
Mapping<br />
�<br />
�<br />
���<br />
�<br />
<strong>The</strong> Ridgeline Manifold<br />
¦<br />
��<br />
�<br />
¨�©<br />
¢<br />
¢¡<br />
�<br />
¢<br />
¦<br />
§<br />
��<br />
¢ �<br />
�<br />
¥<br />
¦<br />
£ ¤<br />
�<br />
¥<br />
��<br />
¢¡ ¢<br />
� ¢�<br />
�<br />
¢ �<br />
¥<br />
¥ ���<br />
� �<br />
�<br />
��<br />
�<br />
�<br />
��<br />
�<br />
��<br />
�<br />
���<br />
�<br />
�<br />
�<br />
��<br />
�<br />
� �<br />
��<br />
<strong>The</strong> image <strong>of</strong> this map will be denoted by and called the ridgeline<br />
surface or manifold. If<br />
one-dimensional curve.<br />
will be called the ridgeline as it is a<br />
¡<br />
©<br />
¦<br />
� it<br />
� �<br />
��<br />
<strong>The</strong>orem 3. <strong>The</strong>n all the critical values <strong>of</strong> the -dimensional multivariate mixture, and<br />
hence modes, antimodes and saddlepoints, are points in .<br />
Surajit Ray Nov 2, 2004<br />
�<br />
�<br />
��<br />
�<br />
�<br />
¥<br />
��<br />
��<br />
�¤£<br />
¢<br />
¢¡<br />
�<br />
¢<br />
�<br />
��<br />
�<br />
�<br />
£<br />
��<br />
���<br />
�<br />
�<br />
�<br />
¢ £<br />
¥ �<br />
��<br />
¥<br />
�<br />
�<br />
�<br />
�<br />
��<br />
¦<br />
§ �<br />
�<br />
�
Ridgeline Curve<br />
Two components, unequal variance:<br />
<strong>The</strong> mixture density with<br />
¢£<br />
¤<br />
¥ ¦<br />
§ §<br />
¨ ©�<br />
� £<br />
¤<br />
¥ ¦<br />
�<br />
y<br />
−1 0 1 2 3<br />
§ �<br />
§��<br />
§<br />
©<br />
¦<br />
¨ ©�<br />
¢�<br />
and<br />
¤<br />
¥ ¦<br />
� �<br />
−2 −1 0 1 2<br />
¡<br />
©<br />
and �<br />
¦<br />
¨ ©�<br />
� �<br />
¥ ¦ �<br />
¤<br />
the following parameters:<br />
Surajit Ray Nov 2, 2004<br />
x<br />
�§<br />
§<br />
�<br />
§<br />
¨ ©�<br />
�<br />
�<br />
¦ � ¥<br />
¤<br />
�<br />
�<br />
�<br />
¨ ©
Ridgeline Elevation Plot<br />
Two components, three modes, unequal variance:<br />
density<br />
0.34 0.36 0.38 0.40 0.42 0.44<br />
replacements<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004
Ridgeline Elevation Plots<br />
Two components, four modes, unequal variance:<br />
��<br />
�<br />
¡¢¡¤£<br />
¥ ¥ ¥<br />
¦ §¢§¤¨<br />
©<br />
� �<br />
�<br />
¡¢¡¤£<br />
�<br />
¥<br />
¥<br />
�<br />
¥<br />
¥<br />
�<br />
�¥<br />
¥<br />
¥<br />
¦ §¢§¤¨<br />
©<br />
��<br />
�<br />
¡¢¡¤£<br />
Surajit Ray Nov 2, 2004<br />
�<br />
�<br />
�<br />
� �<br />
�<br />
� �<br />
�<br />
¦ §¢§¤¨<br />
©<br />
� �<br />
�<br />
¡¢¡¤£<br />
�<br />
�¥<br />
¥<br />
¥<br />
�<br />
¥<br />
¥<br />
�<br />
¥<br />
¥<br />
¦ §¢§¤¨<br />
©<br />
�<br />
�<br />
£<br />
�<br />
� �<br />
�<br />
¦ ¨
density<br />
0.142070 0.142080<br />
density<br />
PSfrag replacements<br />
density<br />
0.136 0.138 0.140 0.142<br />
ments<br />
0.0000 0.0005 0.0010 0.0015 0.0020<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
density<br />
0.137085 0.137095<br />
density<br />
PSfrag replacements<br />
0.10 0.11 0.12 0.13 0.14 0.15 0.16<br />
Surajit Ray Nov 2, 2004
Ridgeline Surface/Manifold<br />
Three components, three modes, equal variance: For<br />
¢ £<br />
¤<br />
¥ ¦<br />
§ §<br />
¨ ©�<br />
y<br />
¢ �<br />
¤<br />
−2 −1 0 1 2 3<br />
¥ ¦<br />
§ ¡<br />
¨ ©�<br />
¢£¢<br />
¤<br />
¥ ¦<br />
¡ §<br />
¨ ©�<br />
−2 −1 0 1 2 3 4<br />
Surajit Ray Nov 2, 2004<br />
x<br />
�<br />
¤<br />
¥ ¦<br />
�<br />
§<br />
�<br />
§<br />
¨ ©�<br />
�<br />
¡<br />
¦<br />
¤<br />
¥ ¤¥¤ ¦<br />
�<br />
,<br />
�<br />
�<br />
¦<br />
¦<br />
¦<br />
¡<br />
¡<br />
¡<br />
§¥§ ©<br />
�<br />
¨<br />
©<br />
¦<br />
,
Ridgeline Contour plot<br />
0.0 0.2 0.4 0.6 0.8<br />
α 3<br />
α 1<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004<br />
α 2
<strong>The</strong> -plots<br />
Ridgeline elevation/contour plots<br />
■ Full information (location and height) <strong>of</strong> the modes and saddle-point.<br />
■ No dependence on � .<br />
-plots<br />
■ Only location <strong>of</strong> the modes and saddle-point not height<br />
■ But extra advantage <strong>of</strong> understanding the dependence on the mixing<br />
parameter �<br />
Surajit Ray Nov 2, 2004
<strong>The</strong> ‘ -equation’<br />
Two component case: If<br />
£¢<br />
¥<br />
¦<br />
Solving we get<br />
if<br />
equation”:<br />
¦<br />
¡<br />
By Construction<br />
1 solution ¦<br />
3 solution ¦<br />
5 solution ¦<br />
¨<br />
�<br />
¢ �<br />
¢¡<br />
¢<br />
¥ is<br />
a critical value <strong>of</strong><br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
£<br />
¥<br />
¥<br />
¡�<br />
¢ �<br />
¢¡<br />
¦<br />
¢£ �<br />
¢<br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
� £ ¢<br />
¥<br />
¦<br />
¢£ �<br />
¥<br />
£<br />
¢<br />
¥ if<br />
¦<br />
� �<br />
¢<br />
�<br />
it satisfies<br />
is a critical value then it solves the “pi-<br />
¡<br />
¡<br />
¡<br />
¢�<br />
¥<br />
¦<br />
� �<br />
1 mode<br />
2 mode<br />
3 mode<br />
Surajit Ray Nov 2, 2004<br />
¢�<br />
¥<br />
¢<br />
¥<br />
�<br />
¦<br />
¦<br />
�<br />
�<br />
�<br />
¢<br />
¥<br />
¥<br />
¥<br />
¢� �<br />
�<br />
�<br />
£
<strong>The</strong> ‘ -equation’<br />
Two component case: If<br />
£¢<br />
¥<br />
¦<br />
Solving we get<br />
if<br />
equation”:<br />
¦<br />
¡<br />
By Construction<br />
1 solution ¦<br />
3 solution ¦<br />
5 solution ¦<br />
¨<br />
�<br />
¢ �<br />
¢¡<br />
¢<br />
¥ is<br />
a critical value <strong>of</strong><br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
£<br />
¥<br />
¥<br />
¡�<br />
¢ �<br />
¢¡<br />
¦<br />
¢£ �<br />
¢<br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
� £ ¢<br />
¥<br />
¦<br />
¢£ �<br />
¥<br />
£<br />
¢<br />
¥ if<br />
¦<br />
� �<br />
¢<br />
�<br />
it satisfies<br />
is a critical value then it solves the “pi-<br />
¡<br />
¡<br />
¡<br />
¢�<br />
¥<br />
¦<br />
� �<br />
1 mode<br />
2 mode<br />
3 mode<br />
Surajit Ray Nov 2, 2004<br />
¢�<br />
¥<br />
¢<br />
¥<br />
�<br />
¦<br />
¦<br />
�<br />
�<br />
�<br />
¢<br />
¥<br />
¥<br />
¥<br />
¢� �<br />
�<br />
�<br />
£
<strong>The</strong> ‘ -equation’<br />
Two component case: If<br />
£¢<br />
¥<br />
¦<br />
Solving we get<br />
if<br />
equation”:<br />
¦<br />
¡<br />
By Construction<br />
1 solution ¦<br />
3 solution ¦<br />
5 solution ¦<br />
¨<br />
�<br />
¢ �<br />
¢¡<br />
¢<br />
¥ is<br />
a critical value <strong>of</strong><br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
£<br />
¥<br />
¥<br />
¡�<br />
¢ �<br />
¢¡<br />
¦<br />
¢£ �<br />
¢<br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
� £ ¢<br />
¥<br />
¦<br />
¢£ �<br />
¥<br />
£<br />
¢<br />
¥ if<br />
¦<br />
� �<br />
¢<br />
�<br />
it satisfies<br />
is a critical value then it solves the “pi-<br />
¡<br />
¡<br />
¡<br />
¢�<br />
¥<br />
¦<br />
� �<br />
1 mode<br />
2 mode<br />
3 mode<br />
Surajit Ray Nov 2, 2004<br />
¢�<br />
¥<br />
¢<br />
¥<br />
�<br />
¦<br />
¦<br />
�<br />
�<br />
�<br />
¢<br />
¥<br />
¥<br />
¥<br />
¢� �<br />
�<br />
�<br />
£
<strong>The</strong> ‘ -equation’<br />
Two component case: If<br />
£¢<br />
¥<br />
¦<br />
Solving we get<br />
if<br />
equation”:<br />
¦<br />
¡<br />
By Construction<br />
1 solution ¦<br />
3 solution ¦<br />
5 solution ¦<br />
¨<br />
�<br />
¢ �<br />
¢¡<br />
¢<br />
¥ is<br />
a critical value <strong>of</strong><br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
£<br />
¥<br />
¥<br />
¡�<br />
¢ �<br />
¢¡<br />
¦<br />
¢£ �<br />
¢<br />
¨<br />
¢<br />
¥<br />
¥<br />
¢<br />
� £ ¢<br />
¥<br />
¦<br />
¢£ �<br />
¥<br />
£<br />
¢<br />
¥ if<br />
¦<br />
� �<br />
¢<br />
�<br />
it satisfies<br />
is a critical value then it solves the “pi-<br />
¡<br />
¡<br />
¡<br />
¢�<br />
¥<br />
¦<br />
� �<br />
1 mode<br />
2 mode<br />
3 mode<br />
Surajit Ray Nov 2, 2004<br />
¢�<br />
¥<br />
¢<br />
¥<br />
�<br />
¦<br />
¦<br />
�<br />
�<br />
�<br />
¢<br />
¥<br />
¥<br />
¥<br />
¢� �<br />
�<br />
�<br />
£
Example:<br />
-plots<br />
<strong>The</strong> mixture density with<br />
¢£<br />
¤<br />
¥ ¦<br />
§ §<br />
¨ ©�<br />
Two components, unequal variance:<br />
y<br />
� £<br />
¤<br />
−1 0 1 2 3<br />
¥ ¦<br />
�<br />
©<br />
§ �<br />
§��<br />
¦<br />
and<br />
§<br />
¨ ©�<br />
¢�<br />
−2 −1 0 1 2<br />
¡<br />
©<br />
and �<br />
¦<br />
¤<br />
¥ ¦<br />
� �<br />
¨ ©�<br />
� �<br />
the following parameters:<br />
Surajit Ray Nov 2, 2004<br />
x<br />
¥ ¦ �<br />
¤<br />
�§<br />
§<br />
¨ ©<br />
§<br />
�<br />
�
Example: -plots<br />
¢<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
£<br />
¡<br />
acements<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004
Example: -plot for unimodal density<br />
¢<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
£<br />
¡<br />
acements<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004
Example: -plot for example with 4 modes<br />
¢<br />
¢<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
£<br />
¡<br />
0.4990 0.5000 0.5010<br />
£<br />
¡<br />
acements<br />
PSfrag replacements<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004
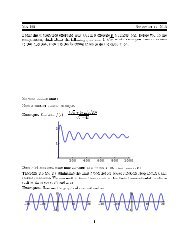
Analytic Solution<br />
From the properties <strong>of</strong> the<br />
by the zeroes <strong>of</strong><br />
Same as the zeroes in<br />
<strong>The</strong>orem 0.1. Let<br />
where<br />
�<br />
¢<br />
¥<br />
Quadratic for Equal Variance<br />
Cubic for Proportional variance<br />
¦<br />
¢£¢ �<br />
¢¡<br />
¥ be the mixture <strong>of</strong> two multivariate<br />
�<br />
£¢<br />
¥<br />
¢<br />
¦<br />
¥<br />
¢<br />
�<br />
¢<br />
¦<br />
¦<br />
�<br />
¥<br />
£<br />
¥<br />
¢<br />
¢ �<br />
¦<br />
£<br />
¢¤<br />
� �<br />
�¤<br />
¢<br />
¦<br />
£<br />
£ �<br />
¢<br />
¥<br />
¡<br />
©<br />
¢ £<br />
¢£ �<br />
¥<br />
� ¢ £ ¢<br />
¤<br />
¥§¦<br />
¨ .<br />
¢<br />
¥<br />
oscillations <strong>of</strong><br />
¦<br />
¢£ �<br />
¦<br />
¢<br />
£<br />
£ �<br />
¢<br />
¥<br />
£ �<br />
¢<br />
¥<br />
¢<br />
¦<br />
¢��<br />
¢<br />
¥<br />
¥<br />
¥<br />
� ¢ £ ¢<br />
¢ �<br />
¢<br />
¥<br />
¦<br />
¢<br />
¢ �<br />
£<br />
£ �<br />
¢<br />
¥<br />
�<br />
¢¤ �<br />
� �<br />
£<br />
¢� �<br />
�¤<br />
� �<br />
¢¤<br />
¦<br />
�<br />
¡<br />
¢<br />
�<br />
¢<br />
�<br />
¥<br />
¢<br />
¥<br />
�¤<br />
� �<br />
¢¤<br />
�<br />
¥<br />
¢<br />
� £ ¢<br />
�<br />
¢ �<br />
¥<br />
¢<br />
� £ ¢<br />
¢<br />
�<br />
�<br />
¥<br />
is determined<br />
normal densities. <strong>The</strong>n<br />
Surajit Ray Nov 2, 2004<br />
¥ £ �<br />
� �<br />
¢£¢ �<br />
¦<br />
¢<br />
�<br />
�<br />
¥
¦<br />
Data Example:Iris Data<br />
§ � direct contour plotting <strong>of</strong> is<br />
Component 2<br />
−3 −2 −1 0 1 2<br />
not available.<br />
CLUSPLOT( iris )<br />
−3 −2 −1 0 1 2 3<br />
Component 1<br />
<strong>The</strong>se two components explain 95.81 % <strong>of</strong> the point variability.<br />
Projection <strong>of</strong> Iris Data on the first two principal-components plane<br />
Surajit Ray Nov 2, 2004
Iris Data: Ridgeline Contour plot<br />
0.0 0.2 0.4 0.6 0.8<br />
α 3<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004<br />
α 1<br />
α 2
¢<br />
£<br />
¡<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Iris Data: -plot<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
¤<br />
acements<br />
¢<br />
£<br />
¡<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
¤<br />
¢<br />
£<br />
¡<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004<br />
¤
Example: Egyptian Skull Data<br />
Egyptian Skull Data: This data consists <strong>of</strong> four measurements Maximal<br />
Breadth, Basibregmatic Height, Basialveolar Length , and Nasal Height <strong>of</strong><br />
male Egyptian skulls from five different time periods ( 4000 BC, 3300 BC,<br />
1850 BC, 200 BC, 150 AD). Thirty skulls were measured from each time<br />
period.<br />
Here we analyze the three earliest time periods<br />
Surajit Ray Nov 2, 2004
Egyptian Skull Data: Ridgeline Contour plot<br />
0.0 0.2 0.4 0.6 0.8<br />
α 3<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004<br />
α 2<br />
α 1
¢<br />
£<br />
¡<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Egyptian Skull Data: Iris Data: -plot<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
¤<br />
acements<br />
¢<br />
£<br />
¡<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
¤<br />
¢<br />
£<br />
¡<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
0.0 0.2 0.4 0.6 0.8 1.0<br />
Surajit Ray Nov 2, 2004<br />
¤
Summary and Future Work<br />
■ For , the problem <strong>of</strong> determining the number <strong>of</strong> modes in the<br />
-dimensional space can be reduced to a 1-dimensional space<br />
¡<br />
©<br />
¦<br />
■ Can be used to determine the number <strong>of</strong> modal clusters<br />
■ Analytical results and dependence <strong>of</strong> modes on the mixing proportion<br />
are discussed in Ray and Lindsay, 2004.<br />
■ Several ways <strong>of</strong> generalization to more than two components.<br />
■ Relating the subspace reduction in discriminant analysis to the<br />
subspace reduction in modality determinantion.<br />
Surajit Ray Nov 2, 2004