PROBLEMA 1 - RESOLUCIÓN. El problema pide la elipse ... - Tecnun
PROBLEMA 1 - RESOLUCIÓN. El problema pide la elipse ... - Tecnun
PROBLEMA 1 - RESOLUCIÓN. El problema pide la elipse ... - Tecnun
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
<strong>PROBLEMA</strong> 1 - RESOLUCIÓN.<br />
Resolución del examen de Febrero 2007 – Problema 1<br />
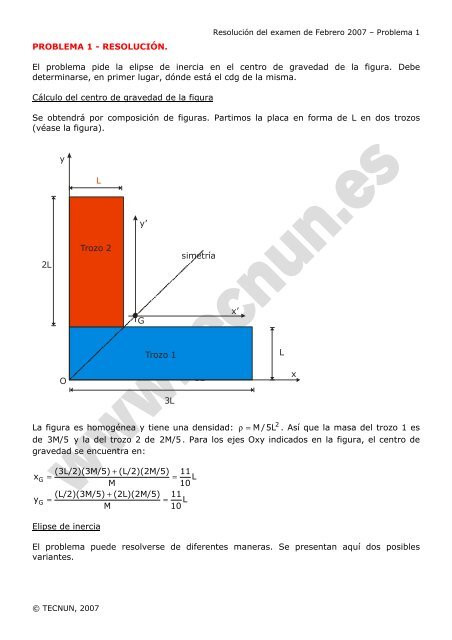
<strong>El</strong> <strong>problema</strong> <strong>pide</strong> <strong>la</strong> <strong>elipse</strong> de inercia en el centro de gravedad de <strong>la</strong> figura. Debe<br />
determinarse, en primer lugar, dónde está el cdg de <strong>la</strong> misma.<br />
Cálculo del centro de gravedad de <strong>la</strong> figura<br />
Se obtendrá por composición de figuras. Partimos <strong>la</strong> p<strong>la</strong>ca en forma de L en dos trozos<br />
(véase <strong>la</strong> figura).<br />
y<br />
L<br />
y’<br />
2L<br />
Trozo 2<br />
simetría<br />
G<br />
x’<br />
Trozo 1<br />
L<br />
O<br />
3L<br />
x<br />
3L<br />
2<br />
La figura es homogénea y tiene una densidad: ρ= M /5L . Así que <strong>la</strong> masa del trozo 1 es<br />
de 3M/5 y <strong>la</strong> del trozo 2 de 2M/5 . Para los ejes Oxy indicados en <strong>la</strong> figura, el centro de<br />
gravedad se encuentra en:<br />
x<br />
y<br />
G<br />
G<br />
(3L/2)(3M/5) + (L/2)(2M/5) 11<br />
= = L<br />
M 10<br />
(L/2)(3M/5) + (2L)(2M/5) 11<br />
= = L<br />
M 10<br />
<strong>El</strong>ipse de inercia<br />
<strong>El</strong> <strong>problema</strong> puede resolverse de diferentes maneras. Se presentan aquí dos posibles<br />
variantes.<br />
© TECNUN, 2007
Resolución del examen de Febrero 2007 – Problema 1<br />
RESOLUCIÓN A – Tensor de inercia de <strong>la</strong> figura en los ejes Oxy<br />
Se trabaja descomponiendo <strong>la</strong> figura en los trozos 1 y 2, calcu<strong>la</strong>ndo los momentos y<br />
productos de inercia de cada trozo en los ejes Oxy indicados en <strong>la</strong> figura, sumando y<br />
tras<strong>la</strong>dando el resultado a los ejes Gx’y’ en el centro de gravedad (que son en los que se<br />
expresará <strong>la</strong> <strong>elipse</strong> de inercia pedida).<br />
La tab<strong>la</strong> muestra los momentos de inercia en los ejes Oxy:<br />
I 2<br />
x<br />
I 2<br />
y<br />
I 2<br />
xy<br />
Trozo 1 Trozo 2 Total<br />
1 26 ML<br />
ML<br />
2<br />
29 ML<br />
2<br />
5<br />
15<br />
15<br />
9 2 ML<br />
ML<br />
2<br />
29 ML<br />
2<br />
5<br />
15<br />
15<br />
9 2 ML<br />
ML<br />
2<br />
17 ML<br />
2<br />
20<br />
5<br />
20<br />
Los momentos de inercia I y de ambos trozos, así como el I x del trozo 1 corresponden a<br />
p<strong>la</strong>cas respecto de ejes que pasan por sus <strong>la</strong>dos (por compresión se asemejan a varil<strong>la</strong>s y<br />
1 2<br />
los momentos de inercia serán de <strong>la</strong> forma M i (longitud) .<br />
3<br />
Los productos de inercia de cada trozo y el momento de inercia I x del trozo 2 se obtienen<br />
tras<strong>la</strong>dando por Steiner los calcu<strong>la</strong>dos respecto de rectas parale<strong>la</strong>s en el centro de<br />
gravedad de dicho trozo:<br />
1 26<br />
I (trozo 2) M (2L) M (2L) ML<br />
12 15<br />
L 3L 9 2<br />
I xy(trozo 1) = 0 + M 1( − )( − ) = ML<br />
2 2 20<br />
L 2 2<br />
I xy(trozo 2) = 0 + M 2( −2L)( − ) = ML<br />
2 5<br />
2 2 2<br />
x = 2 + 2 =<br />
Nótese que si se colocan los ejes paralelos a Oxy en el centro de gravedad de cada trozo<br />
los productos de inercia en esos ejes son nulos.<br />
Los momentos y productos de inercia en los ejes Gx’y’ colocados en el centro de gravedad<br />
se obtendrían también por Steiner:<br />
2 29 2 11 2 217 2<br />
Ix = Ix' + M (y G) → Ix'<br />
= ML − M( L) = ML<br />
15 10 300<br />
2 29 2 11 2 217 2<br />
Iy = Iy' + M (x G) → Iy'<br />
= ML − M( L) = ML<br />
15 10 300<br />
17 11 9<br />
Ixy = Ix'y' + M (xGy G) → Ix'y'<br />
= ML − M( L) = − ML<br />
20 10 25<br />
2 2 2<br />
RESOLUCIÓN B – Tensor de inercia de <strong>la</strong> figura directamente en los ejes Ox’y’<br />
Se descompone <strong>la</strong> figura en los dos trozos 1 y 2 seña<strong>la</strong>dos. Se trabaja con cada trozo por<br />
separado, calcu<strong>la</strong>ndo los momentos de inercia para ejes paralelos a Gx’y’ que pasan por su<br />
© TECNUN, 2007
Resolución del examen de Febrero 2007 – Problema 1<br />
cdg y después se tras<strong>la</strong>dando los resultados a los ejes Gx’y’. Al final se suma <strong>la</strong><br />
contribución de cada trozo a los momentos I x' , I y' y al producto I x'y' .<br />
Trozo 1:<br />
Se colocan unos ejes G 1 x1y1 en el centro de gravedad de dicho trozo (punto ( 3L , L )<br />
2 2 ).<br />
Los momentos y productos de inercia son:<br />
1 2 1 2 L 2 133 2<br />
Ix1 = M 1(L) = ML → Ix ' = Ix1 + M 1(y G − ) = ML<br />
12 20 2 500<br />
1 9 3L 273<br />
I M (3L) ML I I M (x ) ML<br />
12 20 2 500<br />
L 3L 18 2<br />
Ix1y1 = 0 → Ix'y' = Ix1y1 + M 1(y G − )(x G − ) = − ML<br />
2 2 125<br />
2 2 2 2<br />
y1 = 1 = → y ' = y1 + 1 G − =<br />
Trozo 2:<br />
De <strong>la</strong> misma forma, se colocan unos ejes G2x2y2 en el centro de gravedad de dicho trozo<br />
(punto ( L , 2L) ). Los momentos y productos de inercia son:<br />
2<br />
1 2 343<br />
I M (2L) ML I I M (y 2L) ML<br />
12 15 750<br />
1 2 1 2 L 2 133 2<br />
Iy2 = M 2(L) = ML → Iy' = Iy2 + M 2(x G − ) = ML<br />
12 30 2 750<br />
L 27 2<br />
Ix2y2 = 0 → Ix'y' = Ix2y2 + M 1(yG −2L)(x G − ) = − ML<br />
2 125<br />
2 2 2 2<br />
x2 = 2 = → x' = x2 + 2 G − =<br />
Total:<br />
Sumando <strong>la</strong>s contribuciones de cada parte:<br />
217 2<br />
I x' (trozo 1+trozo 2) = ML<br />
300<br />
213 2<br />
I y' (trozo 1+trozo 2) = ML<br />
300<br />
9<br />
I x'y' (trozo 1+trozo 2) =− ML<br />
25<br />
Valores que coinciden con los obtenidos por el procedimiento anterior.<br />
2<br />
La <strong>elipse</strong> de inercia en G será entonces:<br />
2 2<br />
x' y' x'y'<br />
1 = x I + y I − 2xyI<br />
Sustituyendo los valores:<br />
217 2 2 18<br />
1 = (x + y ) + xy<br />
300 25<br />
Nótese que I x = I y , así como que I x' = I y' , lo que resulta coherente por <strong>la</strong> simetría de <strong>la</strong><br />
figura. Asimismo I xy > 0, mientras que I x'y' < 0 (para los ejes en el centro de gravedad de<br />
© TECNUN, 2007
Resolución del examen de Febrero 2007 – Problema 1<br />
<strong>la</strong> figura). Esto resulta coherente con <strong>la</strong> distribución de masa de <strong>la</strong> figura (y recuérdese que<br />
el producto de inercia puede ser negativo).<br />
Momentos principales de inercia en G<br />
Obtenido el tensor de inercia en G los momentos principales podrían obtenerse del cálculo<br />
de valores propios de dicha matriz. <strong>El</strong> procedimiento, aunque correcto, resulta un tanto<br />
engorroso de resolver.<br />
Una alternativa muy interesante consiste en descubrir cuáles son <strong>la</strong>s direcciones principales<br />
de inercia de <strong>la</strong> p<strong>la</strong>ca y calcu<strong>la</strong>r los momentos de inercia asociados a esos ejes (que son los<br />
principales de inercia). La figura muestra cuál es el eje de simetría de <strong>la</strong> p<strong>la</strong>ca, que forma<br />
45º con los ejes x e y respectivamente. Este eje es un eje principal de inercia; el otro será<br />
el perpendicu<strong>la</strong>r. En dichos ejes el producto de inercia es nulo.<br />
Los momentos principales de inercia serán, por lo tanto, los momentos de inercia de <strong>la</strong><br />
figura para dichos ejes. Como se conoce el tensor de inercia en G en los ejes Gx’y’:<br />
2 2<br />
e =α x' +β y' − αβ x'y'<br />
I I I 2 I<br />
siendo α y β los cosenos directores de un vector unitario en <strong>la</strong> dirección del eje:<br />
- Para el primer eje principal de inercia (eje de simetría): α=β=<br />
2<br />
(forma 45º)<br />
2<br />
- Para el segundo eje principal de inercia (perpendicu<strong>la</strong>r): α=−<br />
2 2<br />
; β= (forma 135º<br />
2 2<br />
con Gx’)<br />
Los resultados son:<br />
325 13<br />
I1<br />
= ML = ML<br />
300 12<br />
109 2<br />
I2<br />
= ML<br />
300<br />
2 2<br />
© TECNUN, 2007