Cálculo del Exponente de Hurst mediante Wavelets

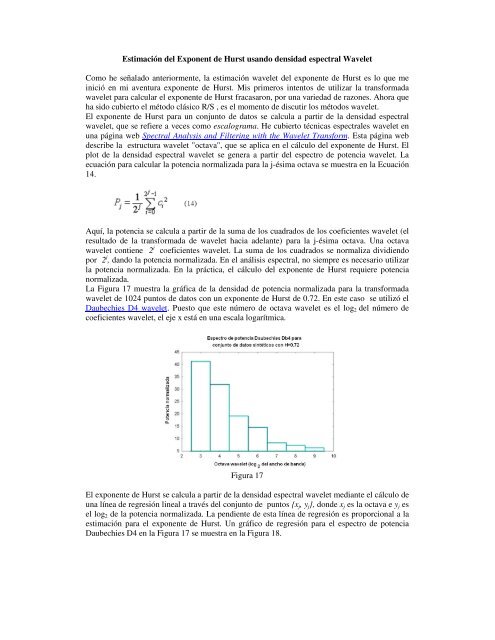
Estimación del Exponent de Hurst usando densidad espectral WaveletComo he señalado anteriormente, la estimación wavelet del exponente de Hurst es lo que meinició en mi aventura exponente de Hurst. Mis primeros intentos de utilizar la transformadawavelet para calcular el exponente de Hurst fracasaron, por una variedad de razones. Ahora queha sido cubierto el método clásico R/S , es el momento de discutir los métodos wavelet.El exponente de Hurst para un conjunto de datos se calcula a partir de la densidad espectralwavelet, que se refiere a veces como escalograma. He cubierto técnicas espectrales wavelet enuna página web Spectral Analysis and Filtering with the Wavelet Transform. Esta página webdescribe la estructura wavelet "octava", que se aplica en el cálculo del exponente de Hurst. Elplot de la densidad espectral wavelet se genera a partir del espectro de potencia wavelet. Laecuación para calcular la potencia normalizada para la j-ésima octava se muestra en la Ecuación14.Aquí, la potencia se calcula a partir de la suma de los cuadrados de los coeficientes wavelet (elresultado de la transformada de wavelet hacia adelante) para la j-ésima octava. Una octavawavelet contiene 2 j coeficientes wavelet. La suma de los cuadrados se normaliza dividiendopor 2 j , dando la potencia normalizada. En el análisis espectral, no siempre es necesario utilizarla potencia normalizada. En la práctica, el cálculo del exponente de Hurst requiere potencianormalizada.La Figura 17 muestra la gráfica de la densidad de potencia normalizada para la transformadawavelet de 1024 puntos de datos con un exponente de Hurst de 0.72. En este caso se utilizó elDaubechies D4 wavelet. Puesto que este número de octava wavelet es el log 2 del número decoeficientes wavelet, el eje x está en una escala logarítmica.Figura 17El exponente de Hurst se calcula a partir de la densidad espectral wavelet mediante el cálculo deuna línea de regresión lineal a través del conjunto de puntos {x j , y j }, donde x j es la octava e y j esel log 2 de la potencia normalizada. La pendiente de esta línea de regresión es proporcional a laestimación para el exponente de Hurst. Un gráfico de regresión para el espectro de potenciaDaubechies D4 en la Figura 17 se muestra en la Figura 18.

Figura 18Si desea una respuesta real, en lugar de una idea de cómo el cambio de una cosa causa el cambiode otra cosa, la afirmación de que algo es proporcional a otra cosa no es muy útil. La ecuaciónpara calcular el exponente de Hurst partir de la pendiente de la línea de regresión a través de ladensidad espectral normalizada se muestra en la Ecuación 15.La Tabla 3 compara la estimación exponente Hurst con tres transformada wavelet para elexponente de Hurst estimado mediante el método R/S. La Daubechies D4 es una transformadawavelet "energía normalizada". Se utilizan aquí también formas de energía normalizadas delwavelet de Haar e interpolación lineal. Un wavelet de energía normalizada parece ser requeridoen la estimación del exponente de Hurst.Table 3 Estimación del exponente de Hurst para 1024 puntos de conjuntos de datos sintéticosFunción Wavelet H=0.5 Error H=0.72 Error H=0.8 ErrorHaar 0.5602 0.0339 0.6961 0.0650 0.6959 0.1079Linear Interp. 0.5319 0.1396 0.8170 0.0449 0.9203 0.0587Daubechies D4 0.5006 0.0510 0.7431 0.0379 0.8331 0.0745R/S 0.5791 0.0193 0.7246 0.0149 0.5973 0.0170El error de la regresión lineal varía mucho para las diversas funciones wavelet. Aunque elwavelet interpolación lineal parece ser un buen filtro para las formas de onda de diente de sierra,como series de tiempo financieras, que no parece funcionar bien para estimar el exponente deHurst.No he descubierto una manera de determinar a priori si una función wavelet dada será un buenestimador del exponente de Hurst, aunque experimentalmente se puede determinar a partir delerror de regresión. En algunos casos también depende del conjunto de datos. En la Tabla 4 elexponente de Hurst se estima a partir de la gráfica de densidad espectral de Haar y a través de latécnica de R/S. En este caso, el wavelet de Haar tenía un error de regresión más bajo que elwavelet Daubechies D4.