Logarithme Népérien

I Définition - Propriétés
Rappel
Logarithme Népérien
La fonction exponentielle est continue , strictement croissante de IR sur ⎤⎦ 0;+∞ ⎡⎣ .
C'est-à-dire (TVI) que pour tout k ∈]0 ; +∞[, l'équation e x = k a une solution unique dans IR.
Définition 1
Cette solution a été notée ln k
On appelle fonction logarithme népérien la fonction qui à un réel x strictement positif, fait correspondre
l'unique réel y tel que e y = x .
La fonction logarithme népérien est notée ln, c'est la fonction réciproque de la fonction exponentielle.
On notera : ]0 ; +∞[→ IR
x ln x
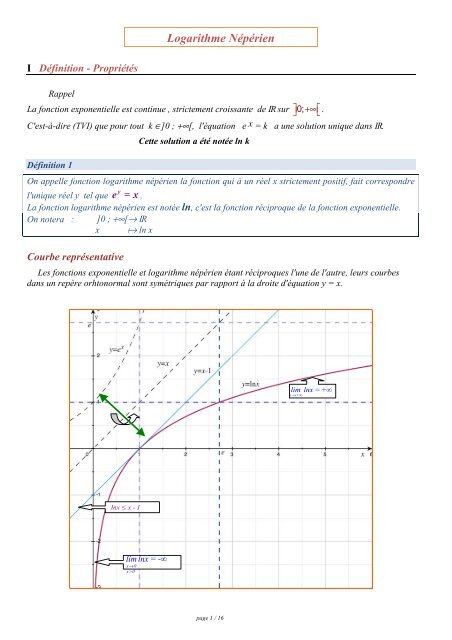
Courbe représentative
Les fonctions exponentielle et logarithme népérien étant réciproques l'une de l'autre, leurs courbes
dans un repère orhtonormal sont symétriques par rapport à la droite d'équation y = x.
lnx ≤ x - 1
lim lnx = -∞
x→0
x>0
page 1 / 16
lim lnx = +∞
x→+∞

On peut conjecturer :
La courbe C de la fonction logarithme népérien est strictement coissante de ]0 ;+∞[ dans ]-∞ ;+∞[.
Elle a pour asymptote verticale l'axe ( Oy )
La courbe d’équattuion : y = ln(x) a pour tangente au point d'abscisse 1 la droite T d'équation y = x-1 .
La courbe se situe au-dessous de cette tangente : pour tout x > 0 , lnx ≤ x - 1 < x
Propriétés 1
• Pour tout réel x strictement positif , on a e ln x = x
• Pour tout réel x, on a ln e x = x
• ln 1 = 0 • ln e = 1
⎧⎪
x ∈⎤⎦ 0;+∞ ⎡
•
⎣ y ∈
⎨
⇔
⎩⎪ y = lnx e y ⎧
⎨
⎩⎪ = x
• La fonction logarithme népérien est une bijection strictement croissante de ]0 ; +∞[ dans IR .
• Par définition si x est un réel strictement positif, ln x est l'unique réel y tel que e y = x
On a donc e ln x = x pour tout x ∈ ]0 ; +∞[ .
• Si x est un nombre réel, ln e x est l'unique réel y tel que e y = e x
Or la fonction exponentielle étant une bijection, e y = e x ⇔ y = x
On a donc ln e x = x pour tout x ∈ IR .
• On sait que e 0 = 1 , on a donc ln 1 = 0
• et e 1 = e donc ln e = 1
⎧
• L'équivalence ⎪x
∈⎤⎦ 0;+∞⎡⎣
y ∈
⎨ ⇔
⎩⎪ y = lnx e y ⎧
⎨
⎩⎪ = x
traduit le fait que les fonctions exponentielle et logarithme népérien sont réciproques l'une de l'autre.
Exercice 1
Déterminer ln e2 ; ln e-3 ; eln 6 ; eln 2 + ln 3
Justifier que ln 6 = ln 2 + ln 3
ln e2 =2 ; ln e-3 = -3 ; eln 6 =6 ; e ln2+ln3 = e ln2 e ln3 = 2 x 3 = 6 = e ln6
donc ln2+ln3 = ln6
e ln5-ln7 = eln5
5
5 7 = = eln donc ln 5 - ln 7 = ln
5
ln7
e 7 7
Exercice 2
Résoudre dans IR les équations : ln x = 4 ; ln x = -2 ; 3 ln x = 2
lnx = 4 ⇔ x = e4 ; lnx = -2 ⇔ x = e -2 2
3 4
; 3lnx = 2 ⇔ x = e ; lnx = 4 ⇔ x = e
Propriétés 2
Pour tous réels a et b strictement positifs on a :
ln( a x b) = ln a + ln b ; ln 1
a
1
= - ln a ; ln = ln a - ln b ; ln a = ln a
a b 2
Pour tout n ∈ ZZ , ln an = n ln a
La démonstration se fait principalement en utilisant les propriétés de la fonction exponentielle.
Soient a et b deux réels strictement positifs on a : e ln a + ln b = e ln a x e ln b = a x b .
page 2 / 16

Sachant que si e x = y , alors x = ln y , on en déduit ln a + ln b = ln (a x b)
e- ln a = 1
=
1
eln a a
e ln a - ln b =
eln a
=
a
eln b b
donc - ln a = ln 1
a
donc ln a - ln b = ln a
b
On peut écrire ln a = ln ( a x a ) = ln a + ln a = 2ln a donc ln a = 1
ln a
2
Pour tout n ∈ZZ , e n ln a = (e ln a ) n = a n donc n ln a = ln a n
Propriété (admise)
Si a 1 , a 2 , ..., a n sont n réels strictement positifs, alors ln (a 1 .a 2 . .a n ) = ln a 1 + ln a 2 + ... + ln a n
Propriétés 3 Équations et inéquations logarithmiques
Équation : ( lna = lnb)
⇔ ( a = b > 0)
Inéquation : ( lna < lnb)
⇔ ( 0 < a < b)
Car la fonction ln est une bijection strictement croissante strictement croissante
⎧lna
= ln b
⎨
⇔
⎩a
> 0 et b > 0
eln a ln b ⎧ = e ⎧a
= b
⎨
⇔ ⎨
⇔ a = b > 0
⎩⎪ a > 0 et b > 0 ⎩a
> 0 et b > 0
⎧lna
≤ ln b
⎨
⇔
⎩a
> 0 et b > 0
eln a ln b ⎧ ≤ e ⎧a
≤ b
⎨
⇔ ⎨
⇔ 0 < a ≤ b
⎩⎪ a > 0 et b > 0 ⎩a
> 0 et b > 0
Exercice 3
Résoudre dans IR les équations : (1) ln x + ln (x - 1) = ln 2 + ln 3 b) (2) ln(x 2 – x) =ln6
⎧x
> 0
⎪
a) (1) ⇔ ⎨x
− 1 > 0
⎪
⎩
ln x(x − 1)
( ) = ln6
⎧x
> 1
⎧x
> 1
⇔ ⎨
aprés résolution : ⎨
⎩x(x
− 1) = 6 > 0
⎩x
= 3 ou x = −2
b) (2) ⇔ x2 − x = 6 > 0 aprés résolution, x = 3 ou x = −2 donc S = −2;3
Exercice 4
Résoudre dans IR les équations :
• lnx + ln(x+4) = ln21 • ln[x(x+4)] = ln7 + ln3
page 3 / 16
{ }
• ln (x 2 + 4x) = ln 21 donc x 2 + 4x = 21 > 0 ou x2 + 4x - 21 = 0
Δ = 16 + 84 = 10 2 −4 + 10
−4 − 10
donc x = = 3 et x = = −7 soit S = −7;3
1 2
2
2
• ln x + ln(x + 4) = ln21
⎧x
> 0
⎪
x > 0
donc ⎨x
+ 4 > 0 ⇔
⎪
x
⎩
ln ⎡⎣ x(x + 4) ⎤⎦ = ln21
2 ⎧
x > 0
⎨
⇔
⎩⎪ + 4x = 21 > 0 x 2 ⎧
⎨
⎩⎪ + 4x - 21 = 0
on a deux solutions : x ⎧⎪
= -7 < 0
1
⎨ Une solution convient : S = { 3}
⎩⎪ x = 3 > 0
2
{ }
donc S = { 3}

Exercice 5
Résoudre dans IR l'équation ln x + ln (4 - x) = ln (2x - 1) + ln 3 (1)
(1)
⇔
⎧x
> 0
⎪
1
⎪4
- x > 0
x ∈
⎨
⇔ 2
⎪2x
-1 > 0
⎩
⎪ln(x(4
- x)) = ln(3(2x -1))
;4
⎤ ⎡
⎥ ⎢
⎦ ⎣
-x 2 ⎧
1
⎪
x ∈
⎨
⇔ 2
⎪
⎩ - 2x + 3 = 0
;4
⎧ ⎤ ⎡
⎪ ⎥ ⎢
⎨ ⎦ ⎣
⎪
⎩
x ∈{ -3;1}
Exercice 6
Résoudre dans IR les équations
• ln ⎜
⎝ ⎛x
+ 1⎞
⎟ = -1
x - 1 ⎠
• ln(x + 1) = -1 + ln(x - 1)
page 4 / 16
donc S = { 1}
• ln ⎜
⎝ ⎛x
+ 1⎞
x - 1
⎟
⎠
= -1 =ln (e-1 )
x + 1 1
e + 1
donc = > 0 ⇔ e(x + 1) = x -1 donc la solution cherchée est x = ≈ -2,16
x -1 e 1- e
• ln(x + 1) = -1 + ln(x - 1) donc ln(x + 1) - ln(x - 1) = -1
⎧
⎪x
+ 1 > 0
⎪
x ∈ 1;+∞
donc ⎨x
-1 > 0 ⇔
⎪x
+ 1 1
⎪ =
⎩ x -1 e
⎤⎦
⎧
⎧
x ∈⎤⎦ 1;+∞⎡
⎪ ⎡⎣ ⎪
⎣
⎨
⇔ ⎨ e + 1 l'équation n'a pas de solution.
⎩⎪ e(x + 1) = x -1 ⎪ x = ≈ -2,16
⎩ 1- e
Exercice 7
Résoudre dans IR les inéquations suivantes :
ln x < 1 2 ln x - 1 ≥ 0 ln (2x - 1) + 1 < 0
a) ln x < 1 ⇔ x < e
b) 2 ln x - 1 ≥ 0 ⇔
1
2lnx ≥ 1 donc lnx ≥
2
1
2 alors x > e ou x > e
c) ln (2x - 1) + 1 < 0 ⇔ ln(2x -1) ≥ -1 et -1 = -lne = lne -1
Exercice 8
Résoudre dans IR les inéquations suivantes :
ln x > ln (2x - 1) ln (1 + e x ) > 0 ln
donc (2x -1) ≥ e-1 > 0 alors 2x > 1 e + 1
+ 1 ou x >
e 2e
1 + e x
< 1 2lnx ≤ ln(3x+4)
1 - e x
⎧ 1
⎧2x
-1 > 0 ⎪x
>
a) ln x > ln (2x - 1) ⇔ x > 2x -1 > 0 ⇔ ⎨ ⇔ ⎨ 2 donc x ∈
⎩x
> 2x -1 ⎪
⎩x
< 1
1
2 ;1
⎤ ⎡
⎥ ⎢
⎦ ⎣
b) ln (1 + e x ) > 0 et 0 = ln 1 donc 1+ e x > 1 donc e x > 0 ce qui est vraie pour tout x réels
c) On pose X = e x 1+ X
1+ X
> 0 et on résout : ln < lne ,(1) ⇔ 0 < < e
1- X 1- X
⎧
⎪X
> 0
⎪
⎪1+
X ⎧X
< 1 et X > 0 X ∈ 0;1
(1) ⇔ ⎨ > 0 ⇔ ⎨
⇔
⎪ 1- X ⎩1+
X < e(1- X)
⎪1+
X
< e
⎩⎪
1- X ⎤
⎧
⎧
X ∈⎤ ⎪ ⎦
⎡
⎦0;1⎡
⎣ ⎪ ⎣
⎨
⇔ ⎨ e -1
⎩⎪ X(1+ e) < e -1 ⎪X
< < 1
⎩ e +1

donc X = e x <
e -1 ⎛ e -1 ⎞
donc x < ln
e +1 ⎝
⎜ e +1⎠
⎟
⎤ ⎛ e -1 ⎞ ⎡
ou x ∈⎥-∞;ln ⎝
⎜ e +1⎠
⎟ ⎢
⎦
⎣
x > 0
e) 2ln x ≤ ln(−3x − 4) ⇔
x 2 ⎧
x > 0
⎨ ⇔
⎩⎪ ≤ 3x + 4 x 2 ⎧
⎧⎪
x > 0
⎨
⇔ ... ⎨
⎩⎪ − 3x − 4 ≤ 0 ⎩⎪ x ∈⎡⎣ −1;4 ⎤⎦ donc x ∈⎤⎦ 0;4⎤⎦
Exercice 09
Écrire plus simplement : a) ln 14 - ln 7 = ln2; b)ln 5 2
+ ln
2 5
page 5 / 16
⎛ 5 2⎞
= ln ×
⎝
⎜ 2 5⎠
⎟
= ln1 = 0; c) ln100
ln10
d) ln8 − ln12 + ln15 = 3ln 2 − (2ln2 + ln3) + ln3 + ln5 = ln 2 + ln5; e) ln10000 − ln0,01 = ln100
Exercice 10
Démontrer que pour tout réel x, on a : ln (1 + e x ) = x + ln (1 + e -x )
ln (1 + e x ) =ln (e x (e –x +1) =lne x +ln(e –x +1) = x+(e –x +1)
II Étude de la fonction logarithme népérien
Propriété 4
• La fonction ln est strictement croissante sur ]0 ; +∞[
• si x > 1 alors ln x > 0 • si 0 < x < 1 alors ln x < 0
• La fonction ln est continue et dérivable sur ]0 ; +∞[ et on a (ln x)’ = 1
x
• lim lnx = +∞ •
x→+∞
lim lnx = - ∞
x→0
x>0
= ln102
ln10
= 2ln10
ln10
• si x > 1 on a alors ln x > ln 1 c'est-à-dire ln x > 0
• si 0 < x < 1 alors ln x < ln 1 c'est-à-dire ln x < 0
• sachant que e ln x = x, en utilisant la propriété de dérivation des fonctions composées,
on peut écrire (e ln x )' = (ln ' x) x e ln x donc (x)' = (ln ' x) x x c'est-à-dire ln ' x = 1
x
la fonction logarithme népérien étant la réciproque de la fonction exponentielle, on peut déduire ses
limites du tableau de variation de la fonction exponentielle.
• Tableau de variations de la fonction ln :
Propriété 5
• lim
x→0
ln(x +1)
= 1
x
x 0 1 e +∞
Signe de f’(x)
1
=
x
Variation de
f(x) = lnx
-∞
+ 1 +
0
1
e +
1
+∞
= 2
• ln(1 + x) a pour approximation affine x au
voisinage de 0.
• On sait que ln' x = 1
. Le nombre dérivé de la fonction ln en 1
x
est donc 1
= 1.
1

Par définition du nombre dérivé, on peut donc écrire
Donc
lim
ln (1 + h)
= 1 ou encore
h→0 h
lim
h→0
lim
ln (1 + x)
= 1.
x→0 x
page 6 / 16
ln (1 + h) - ln 1
= 1
h
• Pour une fonction f dérivable en x 0 , l'approximation affine de f(x 0 + h) est f(x 0 ) + f'(x 0 ) x h
L'approximation affine de ln(1 + h) est donc ln 1 + ln' (1) x h = 0 + h = h
L'approximation affine de ln(1 + x) au voisinage de 0 est donc x .
Cela revient à dire que la courbe de la fonction ln a pour tangente au point d'abscisse 1 la droite d'équation y = x-1
Propriété 6 Croissance comparée
•
lnx
lim = 0 •
x→+∞ x
lim xlnx = 0
x→0
x>0
Au voisinage de l'infini x l'emporte sur le logarithme népérien de x.
• Pour déterminer
lim
x→+∞
ln x
x , posons X = ln x on a alors eX = x
Lorsque x tend vers +∞ , ln x tend vers +∞, donc X tend vers +∞.
On peut écrire
Or on sait que
• Pour déterminer
ln x
x
lim
X→+∞
=
X
donc lim
eX x→+∞
eX
= +∞ donc
X
ln x
x =
lim
X→+∞
lim x ln x = 0 , posons X =
x→0
x >0
1
x
lim
X→+∞
X
.
eX X
= 0 et par conséquent
eX on a alors x = 1
X
lim
X→+∞
Lorsque x tend vers 0 par valeurs positives , 1
tend vers +∞, donc X tend vers +∞
x
On peut écrire x ln x = 1
ln
1
= -
1
ln X = -
ln X
X X X X
Or on sait que
lim
X→+∞
ln X
= 0 donc
X
lim
X→+∞
- ln X
X
= 0 et par conséquent
ln x
= 0 .
x
lim x ln x = 0 .
x→0
x >0
lnx
Remarque : On a vu que lim = 0
x→+∞ x
On dit que la courbe a pour direction asymptotique l'axe (Ox) au voisinage de +∞
Propriété 7
Si u est une fonction dérivable et strictement positive sur un intervalle I, la fonction ln o u qui à x
associe ln(u(x)) est dérivable sur I, et on a : (ln o u)' = u'
u
La fonction ln étant dérivable sur ]0 ; +∞[.
L’application de la propriété de dérivation des fonctions composées permet d'affirmer que si u est une fonction
dérivable et strictement positive sur un intervalle I, la fonction
ln o u qui à x associe ln(u(x)) est dérivable sur I, et on a : (ln o u)' = u' x ln' o u = u' x 1
=
u'
u u
Remarque si u < 0 sur I lno(-u) est dérivable sur I et (lno(-u))’= -u' u'
=
-u u
Propriété 8
Si u est une fonction dérivable non nulle sur un intervalle I,

La dérivée de ln u
sur I est
Exercice 11
u'
u
. Donc une primitive de
page 7 / 16
u'
u
sur I, est ln u
Pour chacune des fonctions suivantes, indiquer dans quel(s) intervalle(s) elle est dérivable et calculer sa
dérivée.
a) f(x) = ln (3x - 1) b) h(x) = ln(x2 ) c) f(x) = 2x + 1 + ln x d) g(x) = ln (1 + x2 ) e)
h(x) = ln (2x - x2 ) f) f(x) = x ln x - x g) g(x) =
2 ln (x + 1)
x + 1
h) h(x) = ln(1 + x ) i)
f(x) = ln(e x + 1) j) g(x) = x 2 + (ln x) 2 k) h(x) = e x ln x
a) f(x) = ln (3x - 1)
1
f est dérivable si 3x-1>0 donc pour x > et f '(x) =
3
3
3x -1
b) h(x) = ln(x2 )
h est dérivable pour x non nul et h'(x) = 2
x
c) f(x) = 2x + 1 + ln x il faut que x > 0 et f'(x) = 2 + 1
x
d) g(x) = ln (1 + x2 ) dérivable sur R et g'(x) = 2x
1+ x 2
e) h(x) = ln (2x - x2 ) dérivable sur 0;2 ⎤⎦
-2x + 2
⎡⎣ et h'(x) =
2x - x 2
f) f(x) = x ln x – x est dérivable pour x > 0 et f '(x) = 1lnx + x 1
-1 = lnx
x
2ln(x + 1)
f(x) = , est dérivable pour x+1> 0 donc pour x > -1
g) x + 1
1
(x + 1) - ln(x + 1)
et f '(x) = 2 x + 1
(x + 1) 2
⎛
⎞
⎜
⎟ 1- ln(x + 1)
⎜
⎟ = 2
⎜
⎟ (x + 1)
⎝
⎠
2
⎛ ⎞
⎝
⎜
⎠
⎟
h) h(x) = ln(1 + x ) est dérivable pour x≥0 et
1
f'(x) =
2 x
1+ x =
1
2 x(1+ x) =
1
2x + 2 x
i) f(x) = ln(e x + 1) est dérivable pour tout x réels car 1+e x > 0 et f'(x) = ex
e x + 1
j) g(x) = x2 + (ln x) 2 est dérivable pour tout x > 0 et f'(x) = 2x + 2lnx × 1 ⎛ ⎞
⎝
⎜ x ⎠
⎟
k) h(x) = e x ln x est dérivable pour tout x > 0 et
Exercice 12
a) Soit f(x) =
2
x - 3
f'(x) = e x lnx + ex
x
Trouver une primitive de f(x) sur ]3 ;+∞[ et sur ]-∞ ;3[
= 2x + 2 lnx
x

x - 1
b) Soit f(x) =
x +1
Trouver une primitive de f(x) sur ]-1 ;+∞[
x
c) Soit f(x) =
2 + x - 2
x +1
Trouver une primitive de f(x) sur ]-1 ;+∞[
x - 1
d) Soit f(x) =
2
(x +1)
Trouver une primitive de f(x) sur ]-1 ;+∞[
a) si x > 3 on pose u = x - 3 > 0 , u' = 1 et f(x) = 2 u'
u
si x > 3 , x - 3 < 0 , donc F(x) = 2ln u et F(x) = 2ln(3- x)
page 8 / 16
donc F(x) = 2ln u et F(x) = 2ln(x - 3)
b) si x > -1 , f(x) = 1- 2 1
x + 1
on pose u = x + 1 > 0 , u' = 1 et f(x) = 1- 2 u'
x(x + 1) - 2
c) si x > 1 , f(x) = = x - 2 donc F(x) = x - 2ln u(x) et F(x) = x - 2ln(x + 1)
x + 1
u 1
x + 1
on pose u = x + 1 > 0 , u' = 1 et f(x) = x - 2 u'
u
d) si x > 1 , On cherche a et b tels que f(x) = a
x + 1 +
donc a = 1 et a + b = -1 donc b = -2 et f(x) = 1
- 2
x + 1
on pose u = x + 1 > 0 , u' = 1 et f(x) = u'
u
Exercice 13
Déterminer les limites suivantes :
lim
x→0
x>0
(x - ln x)
lim
x→+∞ ln (1 + 1 + x2 )
lim
x→+∞
a)
b)
( x - ln x )
lim (x - ln x) =0+∞=+∞
x→0
x>0
lim
x→0
x>0
c) lim
x→+∞
d)
ln x
x
= ( lim lnx )(
x→0
x>0
( ln x +
1
- 1 ) = +∞
x
lim
x→+∞ ln (1 + 1 + x2 )
1
lim
x→0 x
x>0
)=-∞
- 2 u'
u
lim
x→0
x>0
donc F(x) = 1
2 x2 - 2ln u(x) et F(x) = 1
2 x2 - 2ln(x + 1)
b a(x + 1) + b
= 2
(x + 1) (x + 1) 2 x -1
=
(x + 1) 2
1
(x + 1) 2
⎛ -1 ⎞
donc F(x) = ln u(x) - 2
2
⎝
⎜ u(x) ⎠
⎟
ln x
x
et F(x) = ln(x + 1) + 2
x + 1
lim
x→+∞
lim ln (1 + 1 + x
x→−∞
2 ) lim
x→0
lim
x→+∞
( x + 1
x
lim 1+ 1+ x
x→+∞
2 ⎧
⎪
= +∞
⎨
lim lnx = +∞
⎩
⎪
x→+∞
+
ln x
)
x2 lim
x→0
x>0
( ln x +
1
- 1 )
x
ln (1 + 1 + x 2 )
(x + 1
x
+
ln x
)
x2 donc ( th lim de fct composées) lim ln(1+ 1+ x
x→+∞
2 ) = +∞

e)
f)
g)
h)
lim
x→−∞ ln (1 + 1 + x2 )=
lim
x→0 ln (1 + 1 + x2 )= ln (1 + 1 ) = ln2
lim
x→+∞
i)
lim
x→0
x>0
lim
x→+∞
lim
x→+∞
lim
x→0
x>0
lnx
lnx
x
( x - ln x ) =
( x + 1
x
+
ln x
)
x2 = 0 et lim
2
x x→+∞
(x + 1
x +
lnx
) 2
x
2 = -∞ et lim
x→0
x>0
lim
x→+∞
lim ln (1 + 1 + x
x→−∞
2 )=+∞
x 1- lnx ⎛ ⎛ ⎞ ⎞
⎜
⎝ ⎝
⎜ x ⎠
⎟ ⎟
⎠
1
= 0 donc par somme, lim
x x→+∞
lnx
or lim
x→+∞ x
⎛
⎝
⎜
x + 1
x
page 9 / 16
= 0 donc lim ( x - lnx)
= lim x = +∞
+ lnx
x 2
1
= +∞ donc on a une forme indétèrminée
x
( )
x + 1 lnx 1
+ = 2
x x x 2 x3 + x 2 + lnx
lim x
x→0
x>0
3 + x 2 ( ) = 0⎞
⎟
⎟ Par somme lim
x→0
lim lnx = -∞ ⎟
x>0
x→0
x>0
⎠
x 3 + x 2 ⎧
⎪
⎪
⎪
⎨
⎪
⎪ 1
lim = +∞
⎪x→0
2
x
⎩x>0
+ lnx
Exercice 13
( ) = -∞
On considère la fonction f définie sur ]0 ; +∞[ par f(x) =
Faire l'étude et la représentation graphique de f.
On considère la fonction f définie sur ]0 ; +∞[ par f(x) =
a) Limites :
1 + ln x
x
⎞
⎠
⎟
x→+∞
= lim x = +∞
x→+∞
⎛
par produit lim
⎝
⎜
1 + ln x
x
x→0
x>0
x + 1
x
lim
1 lnx
f(x) = lim + lim = 0 + 0 = 0 la droite y=0 est asymptote à (C) en +∞
x→+∞ x→+∞ x x→+∞ x
⎛ 1 ⎞
lim f(x) = lim (1+ lnx)
x→0 x→0 ⎝
⎜ x ⎠
⎟
x>0
x>0
or
⎧ 1
⎪lim
= +∞
⎪ x→0 x
x>0
⎨
donc lim f(x) = -∞
x→0
⎪lim(1+
lnx) = -∞ x>0
x→0
⎩⎪
x>0
b) Variations de f
⎛ 1+ lnx ⎞
f'(x) =
⎝
⎜ x ⎠
⎟ ' =
1
x - (1+ lnx)
x
x 2
si x ∈⎤⎦ 0;1⎡⎣
alors f '(x) > 0 et f croissante
si x ∈⎤⎦ 1;+∞⎡⎣
alors f '(x) < 0 et f est décroissante
c) Tableau de variation de f
x 0 1 +∞
= - lnx
donc f ' a le signe de -lnx
2
x
+ lnx
x 2
x→+∞
⎞
⎠
⎟ = -∞

f ’(x) + 0 -
Variation
de f
d) Représentation graphique
Exercice 14
1
-∞ 0
On considère la fonction f définie sur ]0 ; +∞[ par f(x) = ln x - 3(ln x) 2
Faire l'étude et la représentation graphique de f. Etudier le signe de f(x) pour x ∈ ]0 ; +∞[.
On considère la fonction f définie sur ]0 ; +∞[ par f(x) = ln x - 3(ln x) 2
Étude et la représentation graphique de f.
a) Limites :
Limites en zéro
f(x) = (lnx) 2
lim(lnx)
x→0
⎛ 1 ⎞
- 3
⎝
⎜ lnx ⎠
⎟ : lim lnx = -∞,
x→0 2 ⎧ = +∞
⎪
⎨ ⎛ 1 ⎞ donc par produit lim f(x) = -∞
x→0
⎪lim
- 3
x→0 ⎝
⎜ lnx ⎠
⎟ = -3
⎩
Limite en +∞ :
lim (lnx)
x→+∞
lim lnx = +∞, donc
x→+∞
2 ⎧ = +∞
⎪
⎨ ⎛ 1 ⎞ donc par produit, lim f(x) = -∞
x→+∞
⎪ lim - 3
x→+∞⎝
⎜ lnx ⎠
⎟ = -3
⎩
b) Variations de f
f '(x) = lnx - 3(lnx) 2 donc f '(x) = 1
1 1
- 3× 2 × ln(x) = ( 1- 6ln(x) )
x x x
Pour x > 0, f '(x) > 0 ⇔ (1- 6ln(x)) > 0 donc si ln(x) < 1
1
6
, c'est à dire si x > e
6
1 ⎤
f est décroissante sur ⎥e
⎦
⎤
f est croissante sur ⎥0;e
⎦
6 ;+∞
1
6
⎡
⎢
⎣
⎡
⎢
⎣
1
⎛
6 et f admet un maximum en e qui vaut : f ⎜ e
⎝
c) Tableau de varaition de f
1
6 0 e
+∞
Signe de f ’(x) + 0 -
Variation de f
1/12
-∞ -∞
Etude du signe de f(x) pour x ∈ ]0 ; +∞[.
X = ln x
⎧X
= ln x
f(x) > 0 ⇔ ⎨
⇔
⎩X(1−
3X) > 0 X ∈ 0; 1
⎧
⎪
⎨ ⎤ ⎡
⎪ ⎥ ⎢
⎩ ⎦ 3⎣
f(x) > 0 ⇔ x ∈ e 0 ⎧
1
1
⎤ ⎡ ⎤ ⎡
3
3
⎪
⎥ ;e ⎢ = ⎥1;e
⎢
1
6
⎞
⎟
⎠
page 10 / 16
= 1
6
⎛ 1⎞
- 3
⎝
⎜ 6 ⎠
⎟
2
= 1
12

IV : Logarithme décimal
page 11 / 16