x - College Fonctions usuelles

TS DEVOIR SURVEILLÉ 6 : CORRIGÉ 2004/2005Exercice 1 ROC (2 points)Question de coursOn sait que pour tout t Î [a, b] :(uv)'(t) = u'(t)v(t) + u(t)v'(t)En intégrant de a à b :D'où :Applicationb( utvt ()()) ¢òdt= u¢ò()()d tvt t+ utv () ¢ò()d t ta[ utvt]bbab() () = u¢()()d tvt ta ò+ utv () ¢ò()d t tbau¢ò()()d tvt t = [ utvt ()()]b - utv () ¢ ()d t ta òabababaUne primitive F de la fonction logarithme népérien est donnée, pour x Î + * par :xF(x) = ò lnt dt1On pose : u(t) = ln t v'(t) = 1On détermine ici LA primitivede la fonction logarithme quis'annule en 1.u'(t) = 1 tv(t) = t (à une constante près)D'où : F(x) = [ t ]lnt x x1- ò dt = x ln x - (x - 1) = x ln x - x + 11Exercice 2 QCM (4 points)1. Réponse K K = ( x+)1ò0,19 dx=01é2x ùê + 0,19xú= 1 + 0,19 = 0,69ë 2 û 20Bien que ce ne soit pas nécessaire, détaillons le calcul des autres intégrales :Remarquons que : I =La fonction intégrée est de la forme u ¢uò ee21 d x =xlnxavec u(x) = ln x.2ò ee1xdxln xComme u est positive sur l'intervalle [e ; e 2 ], une primitive de u u¢ est donc ln u d'où :I = [ ln(ln x)] 2Là encore, nous avons la forme u ¢uJ =òln30ex1+exe e= ln(ln(e 2 )) - ln(ln e) = ln 2avec u(x) = 1 + e x d'où :dx= é xln( 1+)ùln3La fonction L est en fait indépendante de sa variable x :L(x) =2 x1 d tx tëò= [ ln ] 2xe = ln 4 - ln 2 = ln 2ûx0t = ln(2x) - ln x = ln 2TS DS - 2004/2005 Page 3 G. COSTANTINI http://bacamaths.net/

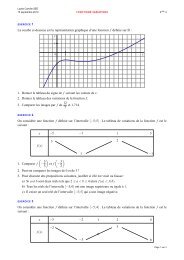
2. Réponse LEn effet, on repère de visu que les 3 premières intégrales sont nulles.I est l'intégrale d'une fonction périodique :I =2pòsin x d x = [ ] 2 p- cos x = 000J est l'intégrale d'une fonction impaire sur un intervalle centré en 0. En effet, posons :¦(x) =xsin1+ x2( x )2pour x Î [-1 ; 1]L'intervalle [-1 ; 1] est symétrique par rapport à 0 et pour tout x de [-1 ; 1], on a :¦(-x) =-xsin1+x2( x )2= -¦(x)D'où : J = 0Ceux qui se sont intéressés à la quadrature de la parabole auront vite repéré que K est nulle :K =æè1 ö d3 ø12ò ç x - ÷ x=0é3x xùê - úë 3 3û10= 0Enfin, bien que ce ne soit pas nécessaire, on peut calculer l'intégrale L par parties :L = l xòxe dx=-1éxëx1e ù - l û -1-1ò e x dx= é( x -1) ex ù =ë û112 - e3. La fonction F est dérivable sur et pour tout x Î :F'(x) =2-xeComme une exponentielle est positive sur , on en déduit :F est croissante sur Pour information : on ne peut pas exprimer la fonction F à l'aide des fonctions usuelles. Il s'agit de lafonction erf (de l'anglais "error function") de Gauss très utilisée en probabilité (loi normale).4. Il s'agit du domaine délimité par la courbe de l'exponentielle, l'axe des abscisses et la droite verticaled'équation x = 0. (La domaine n'est pas délimité sur le côté gauche).On fixe donc un réel A négatif et on calcule l'intégrale :I(A) =0xò e dx= x0éeù = 1 - eë ûAAAPour étudier l'aide du domaine D, il suffit d'étudier la limite de I(A) lorsque A tend vers -¥. Comme cettelimite existe, le domaine a une aire finie (bien qu'il ne soit pas géométriquement borné) :lim I(A) = 1A®-¥L'aire du domaine D = {(x, y) Î 2 , x 0 et 0 y e x } est égale donc égale à :1 u.a.TS DS - 2004/2005 Page 4 G. COSTANTINI http://bacamaths.net/

yC exp11A-3 -2-1OxRemarque : on pouvait faire une estimation graphique pour pencher pour le réponse 1 u.a.Exercice 3 (4 points)On considère les intégrales I et J suivantes :1. On a :I =ò0ln16eexx+ 3 d x+ 4et J =ò0ln161dxxe + 4I - 3J =ò0ln16xedxxe + 4= éln( x + 4) ùln16ëe = ln 20 - ln 5 = ln 4û0I + J =0ln16ò1dx= ln 162. Pour calculer I et J, on résout le système :En soustrayant les deux équations, on obtient :D'où :ìI+ J = ln16íîI- 3J= ln44J = ln 16 - ln 4 = ln 4 = 2 ln 2J = ln22I = 2 ln 2 + 3J = 7ln22TS DS - 2004/2005 Page 5 G. COSTANTINI http://bacamaths.net/

Exercice 4 (10 points)1. a. Pour tout entier n Î , on a :u n+1 - u n =n+1n1åk!- 1åk!= 1( n + 1)!k = 0 k = 0u n+1 - u n 0La suite (u n ) est donc croissante.b. On considère la propriété Ã définie pour tout k Î * par :Ã(k) : k ! 2 k-1· On a Ã(1) puisque : 1 ! 2 0· Supposons Ã(k) pour un certain entier k Î * . Alors :D'où Ã(k + 1)(k + 1)! (k + 1)k!Ã( k)(k + 1) 2 k-1 k+ 12La propriété Ã est initialisée en 1 et héréditaire à partir du rang 1, donc d'après le principe deraisonnement par récurrence, elle est vraie à tous les rangs non nuls. On a donc bien, pour tout k Î * :k ! 2 k-1Par décroissance de la fonction inverse sur [1, +¥[, il vient :En sommant pour k allant de 1 à n :nk = 11k! 112 k -1åk! 1å k -12nk = 12kLe membre de droite est la somme de n termes d'une suite géométrique de raison 1 , il vaut donc :2æ1n 11å k -1k = 12= è2nö- ç ÷ø11-2n( ) 21= 2 1 ( )- 2On a donc :n1åk! 2k = 1Et en ajoutant 1 : u n 3La suite (u n ) est donc bien majorée par 3.c. La suite (u n ) est croissante et majorée, donc elle converge.2. Dans cette question, nous allons calculer la limite de la suite (u n ).Pour cela, on considère, pour tout n Î , la suite (I n ) définie par :I 0 = 1 1-xò e dxet I n = 1 n 1-xx dx0n!òe pour n Î *01a. On a : I 0 =1é1-x-e ù =ë û00é1-xe ù = e - 1ë û1TS DS - 2004/2005 Page 6 G. COSTANTINI http://bacamaths.net/

. Pour tout n Î * et tout x Î [0 ; 1], on a :0 x n 1En multipliant par e 1-x 0 : 0 x n e 1-x e 1-xEn intégrant pour x allant de 0 à 1 :0 1n 1-xòx e dx01 1 -xò e0dxEt en divisant par n ! 0 I n 1 n!1 1 - xò eI0C'est-à-dire : 0 I n n!On en déduit, d'après le théorème de gendarmes que :c. On a : (n + 1)! I n+1 =0lim I n = 0n®+¥ò01xdxn+ 11-xPosons : u(x) = x n+1 et v'(x) = e 1-xUne intégration par parties donne :(n + 1)! I n+1 =edxu'(x) = (n + 1)x n et v(x) = - e 1-xé-ën 1 1 xx + -1e ù + (n + 1)û(n + 1)! I n+1 = -1 + (n + 1)Et en divisant par (n + 1)! : I n+1 = I n -0ò1( n + 1)!d. On considère la propriété à définie pour tout n Î par :• On a Ã(0) puisque :Ã(n) : I n + u n = eI 0 + u 0 = e - 1 + 1 = e· Supposons Ã(n) pour un certain entier n Î . Alors :I n+1 + u n+1 2.c.= I n -01ò01n 1-xx en 1-xx edx1+ u n+1 = I n + u n( n + 1)!dxÃ( n)= eD'après le principe de raisonnement par récurrence, on en déduit que pour tout n Î :I n + u n = ee. On a vu à la question 2.b. quelim I n = 0 et compte tenu du fait que u n = e - I n , nous obtenons :n®+¥lim u n = en®+¥On a montré que :limn®+¥nåk = 01k!= eCe qu'on note encore : e =¥åk=01k!TS DS - 2004/2005 Page 7 G. COSTANTINI http://bacamaths.net/