Fonctions convexes d'une variable réelle ... - CAPES de Maths

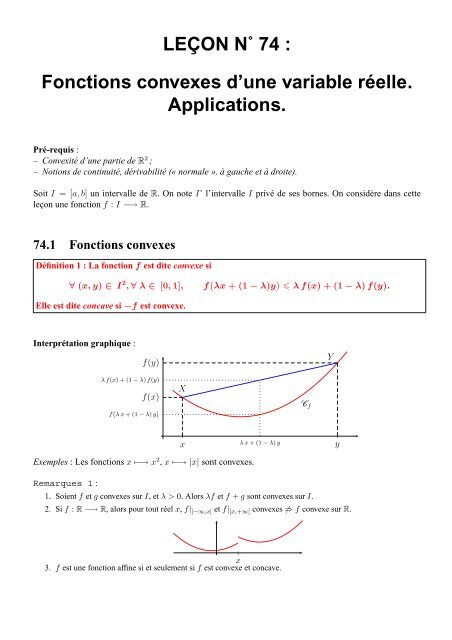
LEÇON N˚ 74 :Fonctions convexes d’une variable réelle.Applications.Pré-requis :– Convexité d’une partie de R 2 ;– Notions de continuité, dérivabilité (« normale », à gauche et à droite).Soit I = [a,b] un intervalle de R. On note I˚ l’intervalle I privé de ses bornes. On considère dans cetteleçon une fonction f : I −→ R.74.1 Fonctions convexesDéfinition 1 : La fonction f est dite convexe si∀ (x, y) ∈ I 2 , ∀ λ ∈ [0, 1],f ( λx + (1 − λ)y ) λ f(x) + (1 − λ) f(y).Elle est dite concave si −f est convexe.Interprétation graphique :f(y)Yλ f(x) + (1 − λ) f(y)f(x)f ( λ x + (1 − λ) y )XC f|xλ x + (1 − λ) y|yExemples : Les fonctions x ↦−→ x 2 , x ↦−→ |x| sont convexes.Remarques 1 :1. Soient f et g convexes sur I, et λ > 0. Alors λf et f + g sont convexes sur I.2. Si f : R −→ R, alors pour tout réel x, f| ]−∞,x[ et f| [x,+∞[ convexes ⇏ f convexe sur R.|x3. f est une fonction affine si et seulement si f est convexe et concave.

2Fonctions convexesThéorème 1 : f est convexe si et seulement si A = {(x, y) ∈ R 2 | f(x) y} est une partie convexede R 2 .démonstration :"=⇒" : Soient M(x 1 , y 1 ), N(x 2 , y 2 ) ∈ A , de sorte que f(x 1 ) y 1 et f(x 2 ) y 2 . On note cesdeux inégalités (⋆). Soit T(x, y) ∈ [MN], on veut montrer que T ∈ A , c’est-à-dire f(x) y.Puisque T ∈ [MN], il existe λ ∈ [0, 1] tel que x = λ x 1 + (1 − λ)x 2 et y = λ y 1 + (1 − λ)y 2 .Alorsf(x) = f ( ) f convexeλ x 1 + (1 − λ)x 2 λ f(x 1 ) + (1 − λ)f(x 2 ) (⋆) λ y 1 + (1 − λ)y 2 = f(y)."⇐=" : Soient (a 1 , a 2 ) ∈ I 2 , M ( a 1 , f(a 1 ) ) , N ( a 2 , f(a 2 ) ) . M, N ∈ A , donc [MN] ⊂ A (car Aest convexe), et par suite, pour tout λ ∈ [0, 1], on aCette appartenance s’écrit aussiT ( λ a 1 + (1 − λ)a 2 , λ f(a 1 ) + (1 − λ)f(a 2 ) ) ∈ A .f ( λ a 1 + (1 − λ)a 2) λ f(a1 ) + (1 − λ)f(a 2 ),donc f est convexe.Notons que A est appelé épigraphe de f.Théorème 2 : Les trois propositions suivantes sont équivalentes :(i) f est convexe ;(ii) Pour tout (x, y, z) ∈ I 3 tel que x < y < z,f(y) − f(x)y − xf(z) − f(x)z − xf(z) − f(y)z − y;(iii) Pour tout x 0 ∈ I, la fonction suivante est croissante :démonstration :(i) ⇒ (ii) :ϕ x0 : I\{x 0 } −→ Rx ↦−→ f(x) − f(x 0)x − x 0.x < y < z et f est convexe, donc il existe λ ∈ [0, 1] tel que(♯){ y = λ x + (1 − λ)zf(y) λ f(x) + (1 − λ)f(z).Par suite, et puisque 1 − λ ≠ 0, on af(y) − f(x)y − x(♯)λ f(x) + (1 − λ)f(z) − f(x)λ x + (1 − λ)z − x− (1 − λ)( f(z) − f(x) )(1 − λ)(z − x)=f(z) − f(x).z − x

3Fonctions convexes(♯) donne aussi, puisque λ ≠ 0,{ ( )x =1 y − (1 − λ)zλf(x) 1 λ(f(y) − (1 − λ)f(z)).En procédent comme tout à l’heure, on obtient alorsf(z) − f(x)z − x(f(y) − (1 − λ)f(z)) f(z) − 1 λz − 1 ( ) =λ y − (1 − λ)zf(z) − f(y).z − y(ii) ⇒ (iii) :Soit (x, y, x 0 ) ∈ I 3 tel que x 0 < x < y. Alors par hypothèse,ϕ x0 (x) = f(x) − f(x 0) f(y) − f(x 0)= ϕ x0 (y).x − x 0 y − x 0De même si x < x 0 < y et x < y < x 0 . On en déduit que ϕ x0 est croissante sur I\{x 0 }.(iii) ⇒ (i) : Soient (x, y) ∈ I 2 tel que x < y, λ ∈ ]0, 1[ et x 0 = λ x + (1 − λ)y ∈ I. D’après (iii), eten notant que x − x 0 < 0, y − x 0 > 0 et y − x > 0, on a :ϕ x0 (x) ϕ x0 (y) ⇔ f(x) − f(x 0)x − x 0 f(y) − f(x 0)y − x 0⇒ (y − x 0 ) ( f(x) − f(x 0 ) ) (x − x 0 ) ( f(y) − f(x 0 ) )⇔ λ(y − x) ( f(x) − f(x 0 ) ) (λ − 1)(y − x) ( f(y) − f(x 0 ) )⇔ λ f(x) + (1 − λ)f(y) (λ − 1 − λ) ( − f(x 0 ) )⇔ λ f(x) + (1 − λ)f(y) f(x 0 ) = f(λ x + (1 − λ)y ) .Remarque 2 : Si l’on note X ( x, f(x) ) , Y ( y, f(y) ) et Z ( z, f(z) ) , alors (i) traduit le fait que la pente de la droite(XY ) est inférieure à celle de (XZ), elle-même inférieure à celle de (Y Z), comme le montre clairement l’illustrationci-dessous :ZXC fY

4Fonctions convexes74.2 Résultats utilesThéorème 3 : Si f : I −→ R est convexe, alors pour tout x 0 ∈ I˚, f admet une dérivée à gauche f ′ get une dérivée à droite f ′ d , f est continue sur I˚ et f ′ g , f ′ dsont croissantes sur I˚.démonstration :• Soit x 0 ∈ I˚. Pour tous x ∈ ]a, x 0 [ et y ∈ ]x 0 , b[, le théorème 2 nous assure que ϕ x0 est croissante etmajorée sur ]a, x 0 [ par ϕ x0 (y). Donc la limite à gauche en x 0 de ϕ x0 existe etlim ϕ f(x) − f(x 0 )xx→x − 0(x) = lim= f0 x→x − 0 x − xg(x ′ 0 ).0On procède de la même manière pour la dérivée à droite, et ces deux résultats amènent directement lacontinuité de f sur I˚.• Soit x 0 ∈ I˚. On a alors que pour tous x ∈ ]a, x 0 [ et y ∈ ]x 0 , b[,f(x) − f(x 0 )x − x 0 f(y) − f(x 0)y − x 0.En passant à la limite (x → x 0 − et y → x 0 + ), on obtient l’inégalité f ′ g(x 0 ) f ′ d (x 0), notée (1). Soitalors x 1 ∈ I˚ tel que x 0 < x 1 . D’après le point (ii) du théorème 2, on a pour tout xin ]x 0 , x 1 [,⇒f(x) − f(x 0 ) f(x 1) − f(x 0 ) f(x) − f(x 1)x − x 0 x 1 − x 0 x − x 1limx→x 0+f(x) − f(x 0 ) f(x 1) − f(x 0 ) limx − x 0 x 1 − x 0 x→x − 1⇔ f ′ d (x 0) f(x 1) − f(x 0 )x 1 − x 0 f ′ g(x 1 ). (2)f(x) − f(x 1 )x − x 1Ainsi, les inégalités (1) et (2) nous donnent f g(x ′ 0 ) f g(x ′ 1 ), ce qui justifie la croissance de f g ′ sur I˚.On procède de la même manière pour fd ′ .Remarques 3 :1. f convexe sur I ⇏ f continue sur I. Considérer par exemple la fonction f définie sur [−1, 1] par f(−1) =f(1) = 2 et pour tout x ∈ ] − 1, 1[, f(x) = x 2 .2. f convexe sur I ⇏ f dérivable sur I. Considérer par exemple la valeur absolue sur un intervalle ouvertcontenant 0.• •

5Fonctions convexesThéorème 4 : Soit f : I −→ R une fonction continue sur I et dérivable sur I˚. Alors f est convexesur I si et seulement si f ′ est croissante sur I˚.démonstration : Le sens direct est assuré par le théorème 3. En effet, puisque f est dérivable sur I˚,on a f ′ g = f ′ d = f ′ sur I˚, ce qui donne directement la croissance de f ′ sur I˚.Démontrons alors le sens indirect. Soient x 1 , x 2 ∈ I tels que x 1 < x 2 et x 0 ∈ ]x 1 , x 2 [. Il existe doncλ ∈ ]0, 1[ tel que x 0 = λ x 1 + (1 − λ)x 2 . On applique le théorème des accroissements finis sur ]x 1 , x 0 [et ]x 0 , x 2 [, de sorte que∃ c 1 ∈ ]x 1 , x 0 [ | f(x 0 ) − f(x 1 ) = f ′ (c 1 )(x 0 − x 1 ) ⇔ f ′ (c 1 ) = f(x 0) − f(x 1 )x 0 − x 1,∃ c 2 ∈ ]x 0 , x 2 [ | f(x 2 ) − f(x 0 ) = f ′ (c 2 )(x 2 − x 0 ) ⇔ f ′ (c 2 ) = f(x 2) − f(x 0 )x 2 − x 0.Puisque f ′ est croissante sur I˚ par hypothèse, et c 1 < c 2 , alorsf ′ (c 1 ) f ′ (c 2 ) ⇔ f(x 0) − f(x 1 )x 0 − x 1 f(x 2) − f(x 0 )x 2 − x 0⇒ λ(x 2 − x 1 ) ( f(x 0 ) − f(x 1 ) ) (1 − λ)(x 2 − x 1 ) ( f(x 2 ) − f(x 0 ) )⇔ f(x 0 ) = f ( λ x 1 + (1 − λ)x 2) λ f(x1 ) + (1 − λ)f(x 2 ),donc f est convexe sur I.Corollaire 1 : Soit f : I −→ R une fonction continue sur I et dérivable sur I˚. Alors f est convexesur I si et seulement si la courbe représentative de f est au-dessus de toutes ses tangentes.démonstration : Soit x 0 ∈ I˚. L’équation de la tangente en x 0 à f est donnée pour tout x ∈ Ipar y = f ′ (x 0 )(x − x 0 ) + f(x 0 ). Soit alors g(x) = f(x) − f ′ (x 0 )(x − x 0 ) − f(x 0 ) définie sur I. gest dérivable sur I˚ et g ′ (x) = f ′ (x) − f ′ (x 0 ). On remarque que g(x 0 ) = 0, et on note C f la courbereprésentative de f. On a alors les équivalences suivantes :⇔⇔f est au-dessus de toutes ses tangentes{ g ′ {< 0 sur ]a, x 0 [ ∀x x0 , fg ′ ⇔′ (x) f ′ (x 0 )> 0 sur ]x 0 , a[ ∀x 0 x, f ′ (x 0 ) f ′ (x)f ′ croissante sur I˚thm 4⇔ f convexe sur I.Corollaire 2 : Soit f : I −→ R est continue sur I et de classe C 2 sur I˚. Alors f est convexe sur I siet seulement si f ′′ est positive sur I˚.démonstration : Le résultat est évident. En effet, le théorème 4 nous assure déjà que f convexe sur Iéquivaut à f ′ croissante sur I˚. Puisque f est C 2 sur I˚, ceci équivaut encore à f ′′ 0 sur I˚.

6Fonctions convexes74.3 Applications74.3.1 ExtremumsProposition 1 : Soient f : I −→ R une fonction dérivable et convexe sur I, et a ∈ I tel quef ′ (a) = 0. Alors f admet un minimum en a.démonstration : D’après le corollaire 1, f est au-dessus de toutes ses tangentes. En particulier, aupoint a, on a donc∀ x ∈ I, f(x) f ′ (a)(x − a) + f(a) = f(a),donc f admet un minimum en a.74.3.2 Inégalité de convexitéExemplesExemple 1 : f(x) = e x définie sur R. f est C 2 , et f ′′ 0 sur R, donc f est convexe. Par le corollaire 1,appliqué en particulier au point d’abscisse nulle, on trouve alors que∀ x ∈ R, f(x) f ′ (0)(x − 0) + f(0) ⇔ e x x + 1.Exemple 2 : g(x) = sin(x) définie sur [0,π/2]. g y est C 2 et g ′′ = − sin 0 sur [0,π/2], donc g est concave.On obtient ainsi la double-inégalité (obtenue de la généralité g concave ⇒ cordes g tangentes) :Convexité avec plusieurs points∀ x ∈[0, π ],22x sin(x) x.πProposition 2 : Soient f : I −→ R convexe, n 2, (λ 1 , x 1 ), . . . , (λ n , x n ) ∈ R × I tels que∑ ni=1 λ i = 1. Alors on a l’inégalité( n)∑f λ i x i i=1n∑λ i f(x i ).i=1démonstration : On procède par récurrence sur l’entier n 2.Initialisation :Pour n = 2, c’est exactement la définition donnée.Hérédité : On suppose le résultat vrai jusqu’au rang n − 1, et l’on se donne (λ 1 , x 1 ), . . .,(λ n , x n ) ∈R × I tels que ∑ ni=1 λ i = 1. Alors⎛⎞( n∑) ( )n∑ λ 1 x 1 + λ 2 x 2n∑f λ i x i = f ⎜ 1 − λ i⎝ 1 − ∑ ni=1 i=3i=3 λ + λ i x i ⎟i ⎠} {{ } i=3=: y( )n∑n∑1 − λ i f(y) + λ i f(x i ).H.R.i=3i=3

7Fonctions convexesOr on a aussi (d’après la formule vraie au rang 2) quef(y) λ 11 − ∑ λ 2ni=3 λ f(x 1 ) +i 1 − ∑ ni=3 λ f(x 2 )i(on aura pris soin de vérifier que la somme des coefficients vaut bien 1), et en remplaçant cerésultat dans l’inégalité obtenue par l’hypothèse de récurrence, on aboutit directement au résultatrecherché.Comparaison de la moyenneProposition 3 : Pour tous x 1 , . . . , x n ∈ R ∗ +, on a la double-inégalité√n√x1 · · · x n x 1 + · · · + x nnx 2 1 + · · · + x2 n.ndémonstration : La fonction ln est concave sur R ∗ +. On a doncn∑i=1( n∑1n ln(x i) lni=1)1n x i⇔⇔( )ln ( n√ x1 + · · · + x nx 1 · · ·x n ) lnnn√ x 1 · · ·x n x 1 + · · · + x n,ncar exp est une bijection strictement croissante. Il ne reste plus qu’à montrer la seconde inégalité, quiest une conséquence de la convexité de la fonction x ↦−→ x 2 . En effet,( n∑i=1) 21n x i n∑i=11n x2 i = x2 1 + · · · + x2 nn⇔x 1 + · · · + x nncar la fonction racine carrée est aussi une bijection strictement croissante.√x2 1 + · · · + x 2 n,nc○ 2011 par Martial LENZEN.Aucune reproduction, même partielle, autres que celles prévues à l’article L. 122-5 du code de lapropriété intellectuelle, ne peut être faite sans l’autorisation expresse de l’auteur.