integration

378 INTEGRAL CALCULUS
At the points of intersection the co-ordinates of the
curves are equal. Since y = x 2 then y 2 = x 4 . Hence
equating the y 2 values at the points of intersection:
x 4 = 8x
from which, x 4 − 8x = 0
and x(x 3 − 8) = 0
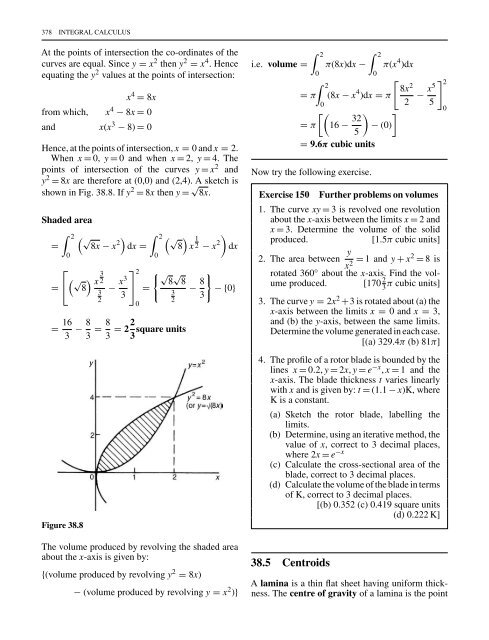
Hence, at the points of intersection, x = 0 and x = 2.
When x = 0, y = 0 and when x = 2, y = 4. The
points of intersection of the curves y = x 2 and
y 2 = 8x are therefore at (0,0) and (2,4). A sketch is
shown in Fig. 38.8. If y 2 = 8x then y = √ 8x.
Shaded area
=
∫ 2
0
⎡
= ⎣ ( 3
√ ) x 2
8
(√
8x − x
2 ) dx =
3
2
⎤
− x3 ⎦
3
2
0
∫ 2
0
(√
8
)
x 1 2 − x 2 )
dx
{√ √ }
8 8
= − 8 −{0}
3
3
2
= 16 3 − 8 3 = 8 3 = 22 square units
3
Figure 38.8
The volume produced by revolving the shaded area
about the x-axis is given by:
{(volume produced by revolving y 2 = 8x)
− (volume produced by revolving y = x 2 )}
i.e. volume =
= π
∫ 2
0
∫ 2
0
π(8x)dx −
∫ 2
0
(8x − x 4 )dx = π
π(x 4 )dx
[(
= π 16 − 32 ) ]
− (0)
5
= 9.6π cubic units
Now try the following exercise.
Exercise 150
[
8x 2
2 − x5
5
Further problems on volumes
1. The curve xy = 3 is revolved one revolution
about the x-axis between the limits x = 2 and
x = 3. Determine the volume of the solid
produced.
[1.5π cubic units]
2. The area between y
x 2 = 1 and y + x2 = 8is
rotated 360 ◦ about the x-axis. Find the volume
produced. [170 2 3π cubic units]
3. The curve y = 2x 2 +3 is rotated about (a) the
x-axis between the limits x = 0 and x = 3,
and (b) the y-axis, between the same limits.
Determine the volume generated in each case.
[(a) 329.4π (b) 81π]
4. The profile of a rotor blade is bounded by the
lines x = 0.2, y = 2x, y = e −x , x = 1 and the
x-axis. The blade thickness t varies linearly
with x and is given by: t = (1.1 − x)K, where
K is a constant.
(a) Sketch the rotor blade, labelling the
limits.
(b) Determine, using an iterative method, the
value of x, correct to 3 decimal places,
where 2x = e −x
(c) Calculate the cross-sectional area of the
blade, correct to 3 decimal places.
(d) Calculate the volume of the blade in terms
of K, correct to 3 decimal places.
[(b) 0.352 (c) 0.419 square units
(d) 0.222 K]
38.5 Centroids
A lamina is a thin flat sheet having uniform thickness.
The centre of gravity of a lamina is the point
] 2
0