integration

384 INTEGRAL CALCULUS
A summary of derive standard results for the second
moment of area and radius of gyration of regular
sections are listed in Table 38.1.
Problem 11. Determine the second moment of
area and the radius of gyration about axes AA,
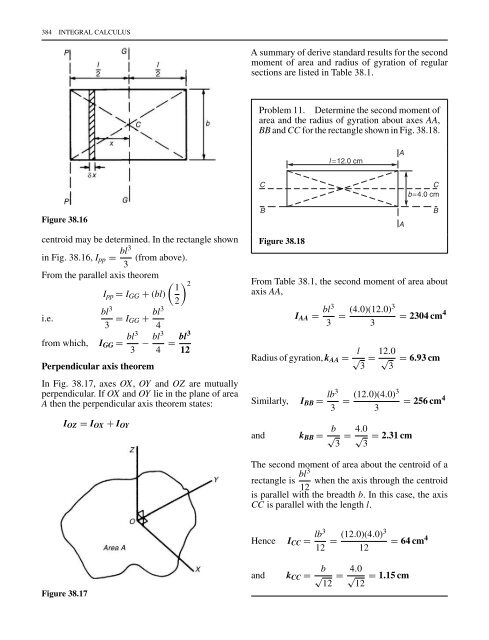
BB and CC for the rectangle shown in Fig. 38.18.
l =12.0 cm
A
C
C
b=4.0 cm
Figure 38.16
centroid may be determined. In the rectangle shown
in Fig. 38.16, I pp = bl3 (from above).
3
From the parallel axis theorem
( 1 2
I pp = I GG + (bl)
2)
bl 3
i.e.
3 = I GG + bl3
4
from which, I GG = bl3
3 − bl3
4 = bl3
12
Perpendicular axis theorem
In Fig. 38.17, axes OX, OY and OZ are mutually
perpendicular. If OX and OY lie in the plane of area
A then the perpendicular axis theorem states:
I OZ = I OX + I OY
B
Figure 38.18
From Table 38.1, the second moment of area about
axis AA,
I AA = bl3
3 = (4.0)(12.0)3
3
Radius of gyration, k AA =
Similarly,
A
B
= 2304 cm 4
l √
3
= 12.0 √
3
= 6.93 cm
I BB = lb3
3 = (12.0)(4.0)3
3
and k BB = b √
3
= 4.0 √
3
= 2.31 cm
= 256 cm 4
The second moment of area about the centroid of a
rectangle is bl3 when the axis through the centroid
12
is parallel with the breadth b. In this case, the axis
CC is parallel with the length l.
Hence
I CC = lb3
12 = (12.0)(4.0)3
12
= 64 cm 4
and k CC = b √
12
= 4.0 √
12
= 1.15 cm
Figure 38.17