θ1 θ2 M m - Politecnico di Torino

Esercizio
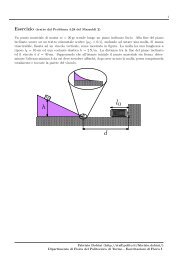
Una ruota di raggio R e di massa M può rotolare senza strisciare lungo un piano inclinato
di un angolo θ2, ed è collegato tramite un filo inestensibile ad un blocco di massa
m, che a sua volta può scivolare su un piano inclinato di un angolo θ1 e privo di attrito.
m
M
θ1 θ2
1. Disegnare le forze che agiscono sul corpo m e scrivere la legge che determina il suo
moto [2 punti];
2. Disegnare le forze che agiscono sul corpo M e scrivere le leggi che determinano il suo
moto [6 punti];
3. Risolvere le equazioni ottenute nei punti precedenti e determinare (in forma simbolica)
l’accelerazione a del sistema e la forza di attrito Fatt in funzione di m, M, θ1, e
θ2 [4 punti];
4. Determinare i valori espliciti di a e di Fatt nel caso particolare in cui m = 5 Kg,
M = 7 Kg, θ1 = π/3 e θ2 = π/6 e commentare se la ruota sale o scende [1 punto];
5. Determinare il valore minimo del coefficiente di attrito (statico o dinamico?) del
piano su cui si trova la ruota, affinché la ruota rotoli senza strisciare (dare espressione
simbolica in funzione di Fatt, M e θ2) [2 punti];
(trascurare la massa delle razze della ruota, e schematizzarla come un anello; momento
d’inerzia dell’anello IA = MR 2 )
SOLUZIONE
Osserviamo anzitutto che, siccome il filo è inestensibile, il sistema si muove solidalmente, e
la velocità e l’accelerazione traslatorie (nelle rispettive direzioni) sono le stesse per l’anello
e per il corpo. Fissiamo un verso convenzionale per l’accelerazione del sistema (ad esempio
quello di discesa lungo il piano per l’anello, e dunque di salita lungo il piano per il corpo,
come mostrato in figura 1).
1. Consideriamo le forze che agiscono sul corpo m. Anzitutto scomponiamo la forza
peso nelle componenti parallela al piano e ortogonale al piano:
Fp1,|| = m g sin θ1
(1)
Fp1,⊥ = m g cos θ1
dove la componenti normale è bilanciata dalla reazione vincolare del piano e non
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
1

ha effetto. Inoltre, agisce la tensione T del filo. L’equazione della dinamica per m,
lungo il piano, è la seguente
−mg sin θ1 + T = ma (moto traslatorio di m) (2)
2. Consideriamo ora le forze che agiscono su M. Scomponiamo la forza peso nelle
componenti parallela al piano e ortogonale al piano:
Fp2,||
Fp2,⊥
=
=
M g sin θ2
M g cos θ2
(3)
dove la componenti normale è bilanciata dalla reazione vincolare del piano e non ha
effetto. Oltre alla forza peso, agiscono anche la tensione T del filo (diretta in maniera
opposta a quella su m), e sul disco anche la forza di attrito (dato che il disco rotola)
che si oppone al moto.
θ1
T
Fp1,⊥ Fp2,⊥
Figure 1:
Fatt
T
F p2,||
• moto traslatorio del centro di massa dell’anello;
Il centro di massa si muove con un moto dettato dalla sommatoria di tutte le
forze che agiscono sul corpo, come applicate al centro di massa stesso:
θ2
Mg sin θ2 − T − Fatt = Ma (4)
• moto rotatorio dell’anello attorno al centro di massa;
Si tratta della equazione del moto rotatorio
M ′E = d L ′E
dove M ′E e L ′E sono il momento delle forze e il momento angolare rispetto al
sistema di riferimento (peraltro non inerziale) del centro di massa dell’anello.
Qui osserviamo che
– per come sono dirette le forze, M ′E e L ′E sono diretti lungo l’asse perpendicolare
al foglio (verso entrante), attorno a cui avviene la rotazione.
dt
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
(5)
2

Proiettando l’equazione vettoriale lungo questa direzione abbiamo
M ′E = dL′E
dt
– L’unica forza che applica un momento è quella di attrito (le altre hanno
braccio nullo)
M ′E = Fatt R (7)
– Il momento angolare lungo l’asse ortogonale al piano dell’anello (un asse
principale) si scrive
L ′E = IA ω ⇒ dL′E
dt = IAα (8)
dove IA è il momento d’inerzia dell’anello, e α è l’accelerazione angolare;
– siccome il moto dell’anello è di puro rotolamento, il punto di contatto è
istantaneamente fermo, e dunque vale la relazione
α = a
(condiz. moto di puro rotolamento) (9)
R
In conclusione, dalle equazioni (6), (7), (8) e (9) ricaviamo che
Fatt R = IA
3. Abbiamo dunque ottenuto le seguenti equazioni [(4), (2) e (10)]
⎧
⎪⎨
a
R
Mg sin θ2 − T − Fatt = Ma
−mg sin θ1 + T = ma
⎪⎩
a
Fatt R = IA
R
che costituisce un sistema di tre equazioni per le tre incognite a, Fatt e T . Risolviamo
il sistema di equazioni; portiamo in evidenza T nella seconda equazione e dividiamo
la terza equazione per R, e
⎧
Mg sin θ2 − T − Fatt = Ma
⎪⎨
T = ma + mg sin θ1
(12)
⎪⎩
Fatt = a IA
R2 Sostituendo la seconda e la terza equazione nella prima e otteniamo
Mg sin θ2 − ma − mg sin θ1 − a IA
= Ma
R2 ⇒ g(M sin θ2 − m sin θ1) = (M + m + IA
)a
R2 ⇒ a = g M sin θ2 − m sin θ1
m + M + IA
R 2
(6)
(10)
(11)
(13)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
3

Ricordando ora che il momento d’inerzia di un anello vale
otteniamo che
IA = MR 2
a = g M sin θ2 − m sin θ1
m + 2M
La forza di attrito si può ora valutare dalla terza delle equazioni (12), ricordando
anche la (14), ossia:
4. Sostituendo i valori numerici
Fatt = a IA
=
R2 = a M =
a = 9.81 m
s 2
= 9.81 m
s 2
= −0.43 m
s 2
= gM M sin θ2 − m sin θ1
m + 2M
7 Kg sin π
π
6 − 5 Kg sin 3
7 1
2 − 5
5 Kg + 2 · 7 Kg
√ 3
2
5 + 14 =
Dal segno si deduce che il verso in cui avviene effettivamente il moto è opposto a
quello inizialmente scelto per a, e dunque la ruota sale.
Per la forza di attrito
=
(14)
(15)
(16)
(17)
Fatt =
=
a M =
−0.43 m
· 7 Kg =
s2 = −3.00 N (18)
in cui il segno meno indica che anche la forza di attrito è diretta in maniera opposta
al verso scelto in figura (dunque è diretta verso il basso), come è corretto che sia, in
quanto si oppone in ogni caso al moto della ruota (che sale).
5. Siccome nel moto di puro rotolamento il punto di contatto rimane istantaneamente
fermo, la forza di attrito che agisce su di esso è una forza di attrito statico. Essa
soddisfa dunque la relazione
|Fatt| ≤ µsFp2,⊥ = µs Mg cos θ2
dove µs è il coefficiente di attrito statico. Pertanto il moto è di puro rotolamento se
µs soddisfa
ossia il valore minimo vale
µs ≥ |Fatt|
Mg cos θ2
µ min
s = |Fatt|
Mg cos θ2
(19)
(20)
(21)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
4

(NOTA BENE: E’ importante notare la differenza tra il presente caso di un anello
che rotola senza strisciare ed il caso di un punto materiale che scriscia lungo un piano
scabro. Per l’anello che rotola senza strisciare la forza di attrito è di tipo statico ed è
un’incognita. Al contrario, se al posto dell’anello avessimo avuto un punto materiale
di massa M, la forza di attrito sarebbe stata di tipo dinamico, e sarebbe stata pari
a µd Mg cos θ, dove µd denota il coefficiente di attrito dinamico.)
Dr. Fabrizio Dolcini
Esercitazioni di Fisica I, Dipart. di Fisica del Politecnico di Torino
5