Le geometrie non euclidee

Eugenio Beltrami (1835-1900)
Scheda: La pseudosfera di Beltrami
Verso la fine degli anni sessanta del XIX secolo, il dibattito sulle geometrie non
euclidee è particolarmente acceso.
Lobacevskj nel 1829 e Bolyai nel 1832 avevano scritto dei saggi in cui
dimostravano la possibilità di geometrie differenti da quella di Euclide, in
particolare geometrie nelle quali il famoso quinto postulato sulle parallele era
diverso da quello euclideo: per un punto esterno a una retta passa più di una
parallela alla retta data.
Le ricerche di questi matematici erano rimaste pressoché ignorate fino a che con
la morte di Gauss (1855) e la pubblicazione del suo epistolario si viene a sapere
che anche il sommo Gauss aveva avuto la stessa idea. L'interesse per questo
problema fa emergere una memoria che Riemann, allievo di Gauss, aveva
scritto nel 1854 ed era rimasta inedita: Sulle ipotesi che stanno a fondamento
della geometria. La memoria pubblicata nel 1867 forniva un nuovo modo di
intendere la geometria. Da un lato presentava la geometria come un caso
particolare di un nuovo concetto matematico, la varietà pluridimensionale;
dall'altro presentava un secondo caso di geometria non euclidea, la geometria
ellittica, nella quale non esistono rette parallele.
Incoraggiato dalle pubblicazioni di personaggi così celebri, il giovane matematico
italiano Eugenio Beltrami si decide a dare alle stampe un suo manoscritto
redatto qualche anno prima e messo da parte per paura delle aspre critiche che
coinvolgevano chi si occupava di geometrie 'astrali' o 'da manicomio'. Il suo
Saggio di interpretazione della geometria non euclidea segna un punto di svolta
nella ricerca geometrica su questo millenario problema.
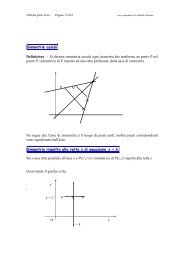
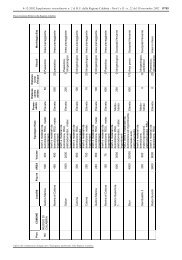
Beltrami aveva trovato un 'substrato reale' per la geometria di Lobacevskj, ossia
aveva trovato all'interno della geometria euclidea, una superficie di rotazione, la
pseudosfera, che poteva essere interpretata come un modello euclideo di
geometria non euclidea. In questo modo dimostrava che la geometria di
Lobacevskj ha lo stesso diritto logico-matematico della classica geometria di
Euclide. Alla superficie aveva dato il nome di pseudosfera perché ha curvatura
costante come una sfera ma di segno negativo.
Per capire come avviene questa 'traduzione' occorre introdurre la nozione di
geodetica. Nel piano il percorso più breve che unisce due punti si trova sulla
retta passante per i due punti. Estendendo questo concetto alle superfici, il
percorso più breve che unisce due punti della superficie si trova su di una linea,
generalmente curva, detta geodetica. Per esempio, dovendosi muovere sulla
superficie di una sfera, il percorso più breve non è quello rettilineo, perché non
esistono percorsi di questo tipo, ma è l'arco di cerchio massimo, che in questo
caso è una geodetica.
La 'traduzione' si ottiene interpretando la superficie pseudosferica come piano di
Lobacevski, le rette di questo piano sono le geodetiche della superficie.