Simmetrie assiali Definizione - Si chiama simmetria assiale ogni ...
Simmetrie assiali Definizione - Si chiama simmetria assiale ogni ...
Simmetrie assiali Definizione - Si chiama simmetria assiale ogni ...
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Affinità parte terza Pagina 13 di 8 easy matematica di Adolfo Scimone<br />
<strong><strong>Si</strong>mmetrie</strong> <strong>assiali</strong><br />
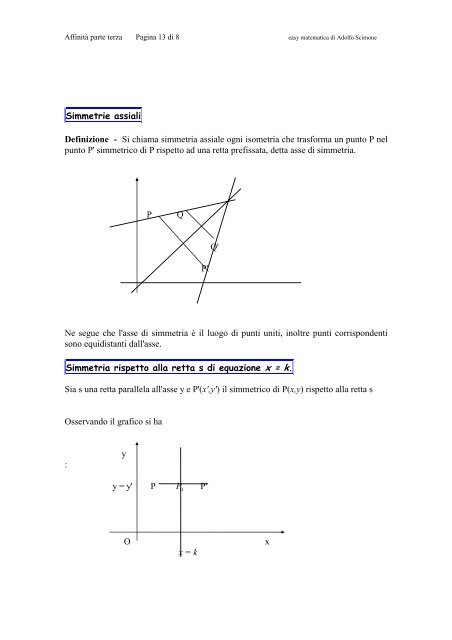
<strong>Definizione</strong> - <strong>Si</strong> <strong>chiama</strong> <strong>simmetria</strong> <strong>assiale</strong> <strong>ogni</strong> isometria che trasforma un punto P nel<br />
punto P' simmetrico di P rispetto ad una retta prefissata, detta asse di <strong>simmetria</strong>.<br />
P Q<br />
P'<br />
Q'<br />
Ne segue che l'asse di <strong>simmetria</strong> è il luogo di punti uniti, inoltre punti corrispondenti<br />
sono equidistanti dall'asse.<br />
<strong>Si</strong>mmetria rispetto alla retta s di equazione x = k.<br />
<strong>Si</strong>a s una retta parallela all'asse y e P'(x',y') il simmetrico di P(x,y) rispetto alla retta s<br />
Osservando il grafico si ha<br />
:<br />
y<br />
y = y' P P 0 P'<br />
O x<br />
x = k
Affinità parte terza Pagina 14 di 8 easy matematica di Adolfo Scimone<br />
y'= y<br />
essendo P0 il punto medio di PP' si ha<br />
⎧ x+ x'<br />
⎪x0<br />
=<br />
⎨ 2<br />
⎪<br />
⎩ y = y'<br />
e quindi<br />
⎧x'=<br />
2k<br />
−x<br />
⎨<br />
⎩y'=<br />
y<br />
dove x = k<br />
0<br />
det A =−1<br />
Se k = 0 si ha la <strong>simmetria</strong> rispetto all'asse y di equazioni<br />
⎧x'=−x<br />
⎨<br />
⎩y'=<br />
y<br />
det A =−1<br />
<strong>Si</strong>mmetria rispetto alla retta r di equazione y = h<br />
Dal grafico si ha<br />
y<br />
P<br />
y = h P 0<br />
⎧ y + y'<br />
⎪y<br />
0 =<br />
⎨ 2 dovey<br />
⎪<br />
⎩x'<br />
= x<br />
e quindi<br />
⎧x'=<br />
x<br />
⎨<br />
⎩y'=<br />
2h−<br />
y<br />
P'<br />
O x = x' x<br />
0<br />
= h<br />
det A =−1
Affinità parte terza Pagina 15 di 8 easy matematica di Adolfo Scimone<br />
Se h = 0 si ha la <strong>simmetria</strong> rispetto all'asse x che ha equazioni :<br />
⎧y'=−y<br />
⎨<br />
⎩x'=<br />
x<br />
det A =−1<br />
<strong>Si</strong>mmetria rispetto alla bisettrice y = x<br />
<strong>Si</strong> dice <strong>simmetria</strong> <strong>assiale</strong> di asse la retta y = x l'isometria di equazione<br />
⎧x'=<br />
y<br />
⎨ det A =−1<br />
⎩y'=<br />
x<br />
come è facile osservare dal grafico.<br />
y<br />
y P y = x<br />
y' P'<br />
O x x' x<br />
<strong>Si</strong>mmetria rispetto alla bisettrice y =− x<br />
<strong>Si</strong> dice <strong>simmetria</strong> <strong>assiale</strong> di asse la retta y =− x l'isometria di equazione<br />
⎧x'=−y<br />
⎨ det A =−1<br />
⎩y'=−x<br />
y<br />
P y<br />
P 0<br />
P' y'<br />
-x' -x x<br />
y = - x
Affinità parte terza Pagina 16 di 8 easy matematica di Adolfo Scimone<br />
<strong>Si</strong>mmetria rispetto alla retta r : y = m x + q<br />
y<br />
P y = m x + q<br />
M<br />
O x<br />
osserviamo che due punti P(x, y) e P'(x',y') sono simmetrici rispetto alla retta r se si<br />
verificano le seguenti condizioni :<br />
⎡1<br />
1 ⎤<br />
• il punto M ( x+ x ) ( y+ y) r<br />
⎣<br />
⎢2<br />
2 ⎦<br />
⎥ ∈<br />
'; '<br />
• P e P' appartengono alla retta perpendicolare ad r.<br />
Queste condizioni si traducono nelle equazioni :<br />
⎧1<br />
1<br />
( y+ y' ) = m⋅ ( x+ x') + q<br />
⎪2<br />
2<br />
⎨<br />
⎪ y−y' 1<br />
=−<br />
⎩⎪<br />
x−x' m<br />
Risolvendo il sistema rispetto a x', y', si ottengono le equazioni della <strong>simmetria</strong> rispetto<br />
alla retta r.<br />
m<br />
x<br />
m x<br />
m<br />
m y<br />
mq<br />
'=<br />
m<br />
−<br />
2<br />
1 2 2<br />
+ −<br />
1+<br />
1+<br />
1+<br />
2m<br />
y'=<br />
1+<br />
m<br />
2 2 2<br />
2<br />
1−<br />
m<br />
x −<br />
1+<br />
m<br />
2<br />
2<br />
2q<br />
y +<br />
1+<br />
m<br />
2<br />
Come caso particolare si possono, da questa, ricavare le simmetrie rispetto alle bisettrici<br />
degli assi.<br />
P'
Affinità parte terza Pagina 17 di 8 easy matematica di Adolfo Scimone<br />
<strong>Si</strong>mmetria centrale o equinversione<br />
<strong>Si</strong> dice <strong>simmetria</strong> centrale di centro C la trasformazione di R 2 in se stesso che porta C in<br />
C e che ad <strong>ogni</strong> punto P ∈R 2 diverso da C, associa il punto P'∈R 2 tale che C sia il<br />
punto medio del segmento PP'.<br />
Se Cx ( 0, y0<br />
) P( x, y)<br />
P( x', y')<br />
si ha<br />
y<br />
⎧ x+ x'<br />
= x<br />
⎪ 2<br />
ϕ : ⎨<br />
⎪ y+ y'<br />
= y<br />
⎩⎪<br />
2<br />
da cui si ottiene<br />
⎧x'=<br />
2x0−x<br />
⎨<br />
⎩y'=<br />
2y0−<br />
y<br />
P(x,y)<br />
Cx ( 0, y0<br />
)<br />
P'(y',x')<br />
O x<br />
0<br />
0<br />
det A = 1<br />
che rappresenta una <strong>simmetria</strong> centrale di centro C che è l'unico punto unito della<br />
trasformazione.<br />
Osservazione<br />
Affinché si abbia una <strong>simmetria</strong> centrale i vettori AB e A' B'<br />
devono essere paralleli.<br />
Se x0 = y0 = 0 si ottiene la <strong>simmetria</strong> rispetto all'origine.<br />
Per verificare se due curve : Γ : y = f ( x) e Γ':<br />
y = f1 ( x)<br />
possiedono un<br />
centro di <strong>simmetria</strong> Cx ( 0, y0<br />
) si pone nella equazione y = f ( x)<br />
1 al posto di x 2x0-x<br />
ed al posto di y 2y0-y e si uguaglia la funzione ottenuta alla f (x) data.<br />
Successivamente , mediante il principio di identità dei polinomi si ricavano i valori di h<br />
e k che soddisfano il sistema.
Affinità parte terza Pagina 18 di 8 easy matematica di Adolfo Scimone<br />
Omografie<br />
Consideriamo il completamento proiettivo P dello spazio affine E con l’aggiunta dei<br />
punti impropri delle rette di E .<br />
<strong>Si</strong> dice omografia di P <strong>ogni</strong> trasformazione biiettiva che trasforma rette proiettive in<br />
rette proiettive. La sua equazione è:<br />
⎧ρ<br />
x<br />
⎪<br />
⎨ρ<br />
x<br />
⎪<br />
⎩ρ<br />
x<br />
'<br />
1<br />
'<br />
2<br />
'<br />
3<br />
= a<br />
= a<br />
= a<br />
11<br />
21<br />
31<br />
x<br />
x<br />
1<br />
x<br />
1<br />
1<br />
+ a<br />
12<br />
+ a<br />
+ a<br />
22<br />
32<br />
x<br />
x<br />
2<br />
x<br />
2<br />
2<br />
+ a<br />
13<br />
+ a<br />
+ a<br />
23<br />
33<br />
x<br />
3<br />
x<br />
x<br />
3<br />
3<br />
ρ ≠ 0 det A ≠ 0<br />
Affinché si abbia un punto unito si dovrà sostituire<br />
'<br />
x 1 con 1<br />
x ecc.<br />
Il sistema omogeneo associato deve ammettere soluzioni non nulle, per cui risulta<br />
necessario e sufficiente che si annulli il determinante dei coefficienti del sistema<br />
a<br />
11<br />
a<br />
a<br />
− ρ<br />
21<br />
31<br />
a<br />
a<br />
22<br />
a<br />
12<br />
− ρ<br />
32<br />
a13<br />
a23<br />
= 0<br />
a − ρ<br />
33<br />
che dicesi equazione caratteristica dell’omografia e ammette tre radici ( x 1,<br />
x2<br />
, x3<br />
) in<br />
generale distinte delle quali nessuna risulta nulla altrimenti sarebbe nullo il determinante<br />
a che è escluso a ≠ 0<br />
ij<br />
Prodotto di affinità<br />
<strong>Si</strong>ano<br />
⎧X<br />
= b11x+ b12 y+ r<br />
ϕ : ⎨<br />
⎩Y<br />
= b21x+ b22 y+ s<br />
e<br />
⎧x'=<br />
a11x+ a12 y+ p<br />
ψ : ⎨<br />
⎩y'=<br />
a21x+ a22y+ q<br />
due affinità del piano in sé, si ha la<br />
ij<br />
(1)<br />
(2)<br />
<strong>Definizione</strong> - <strong>Si</strong> dice prodotto operatorio o semplicemente prodotto di ψ e ϕ e si scrive<br />
ϕ ψ<br />
<br />
l'affinità δ che si ottiene applicando prima ψ e poi ϕ
Affinità parte terza Pagina 19 di 8 easy matematica di Adolfo Scimone<br />
⎧X<br />
= b11( a11x+ a12y+ p) + b12( a21x+ a22 y+ q) + r<br />
δ : ⎨<br />
⎩Y<br />
= b21( a11x+ a12 y+ p) + b22( a21x+ a22 y+ q) + s<br />
⎧X<br />
= ( b11a11 + b12a21) x+ ( b11a12 + b12a22 ) y+ b11p+ b12 + r<br />
δ : ⎨<br />
⎩Y<br />
= ( b21a11 + b22a21) x+ ( b21a12+ b22a22) y+ b21p+ b22q+ s<br />
posto<br />
b11p+ b12 + r = e<br />
b21p+ b22q+ s= f<br />
avremo<br />
⎧X<br />
= ( b11a11 + b12a21) x+ ( b11a12 + b12a22) y+ e<br />
δ : ⎨<br />
⎩Y<br />
= ( b21a11 + b22a21) x+ ( b21a12 + b22a22 ) y+ f<br />
<strong>Si</strong> può provare facilmente che<br />
a) il prodotto di due affinità è un'affinità, per cui l'insieme A delle affinità è chiuso<br />
rispetto all'operazione <br />
b) l'operazione è associativa<br />
ϕ ( ψ δ) = ( ϕ ψ) δ<br />
c) ∀ϕ∈A ∃ un'affinità I ∈ A tale che<br />
I ϕ= ϕ I=<br />
ϕ<br />
−1 −1 −1<br />
d) ∀ϕ ∈A, ∃! ϕ ∈ A: ϕ ϕ = ϕ ϕ = I<br />
Poiché<br />
ϕ ψ≠ ψ ϕ<br />
Il prodotto di affinità non è commutativo.<br />
Pertanto la struttura ( , )<br />
A è un gruppo non commutativo.<br />
Le affinità formano un gruppo rispetto al prodotto di trasformazioni avente come<br />
sottogruppo il ,gruppo delle similitudini e quindi il gruppo delle isometrie.
Affinità parte terza Pagina 20 di 8 easy matematica di Adolfo Scimone<br />
<strong>Si</strong> ha quindi il grafo<br />
Affinità<br />
(geometria affine)<br />
<strong>Si</strong>militudini<br />
(geometria simile gruppo non abeliano)<br />
Isometrie (geometria euclidea) Rotomotetie (gruppo abeliano)<br />
Traslazioni Rotazioni Omotetie<br />
(abeliano) (abeliano) (abeliano)<br />
CAMBIAMENTO DI RIFERIMENTO<br />
Rototraslazione<br />
Per determinare le coordinate del punto P(x, y) rispetto ad un nuovo sistema di<br />
riferimento O ' x ' y ' rototraslato rispetto ad O x y, faremo uso delle formule :<br />
⎧x= x'cosα − y'senα + a ⎧x'<br />
= ( x− a)cos α + ( y−b)senα ⎨ e, viceversa ⎨<br />
⎩y = x'sen α + y'cosα + b ⎩y'<br />
=−( x− a)sen α + ( y−b)cosα che si ottengono dalla composizione dei casi precedenti.<br />
y<br />
Y P<br />
O'<br />
N M<br />
X<br />
α<br />
O H K x