Le geometrie non euclidee

Le geometrie non euclidee
(dal sito http://www.matematicamente.it)
Le geometrie non euclidee partono da postulati opposti a quello di Euclide sulla rette parallele, in particolare dalle due
negazioni possibili del V postulato.
Un modo equivalente per esprimere questo postulato di Euclide è il seguente:
P1) In un piano, per un punto esterno a una retta data esiste un'unica retta passante per il punto dato e parallela
alla retta data.
Un teorema che consegue da questo postulato è il seguente:
T1) In un triangolo, la somma degli angoli interni è 180°.
Nel 1829, N. Lobacevskij, e più o meno contemporaneamente l'ungherese J. Bolyai, costruirono una geometria, risultata
poi altrettanto coerente matematicamente di quella di Euclide, secondo la quale
P2) per un punto esterno a una retta data passa più di una retta parallela (se ne esiste più di una ne esistono
infinite).
Come conseguenza,
T2) in un triangolo, la somma degli angoli interni è minore di 180°
Nel 1854, B. Riemann, in uno studio globale sulla geometria, ipotizzo la possibilità di una terza geometria, nella quale
P3) per un punto esterno a una retta data non passa alcuna parallela.
Come conseguenza,
T3) in un triangolo, la somma degli angoli interni è maggiore di 180°.
Le tre geometrie sono state più correttamente definite da F. Klein, rispettivamente, geometria parabolica, iperbolica ed
ellittica.
Per immaginare le due geometrie distinte da quella euclidea si può fare ricorso a dei 'modelli'.
Per la geometria ellittica o riemanniana, Invece del piano consideriamo la superficie di una sfera e traduciamo gli elementi
geometrici del piano in corrispondenti elementi geometrici sulla superficie della sfera.
I punti del piano corrispondono a punti della superficie della sfera. Le rette del piano corrispondono alle circonferenze
massime della superficie sferica. In generale, si fanno corrispondere alle rette del piano le linee geodetiche di una
superficie curva. Queste ultime infatti conservano la principale caratteristica delle rette e precisamente sono le linee più
brevi che sulla superficie congiungono due punti dati. Sulla superficie della sfera le geodetiche sono proprio le
circonferenze massime, cioè quelle circonferenze che si ottengono intersecando la superficie della sfera con piani
passanti per il centro della sfera. Esempi familiari sono i meridiani e l'equatore, non lo sono i paralleli.
Sulla superficie della sfera non esistono 'rette' o meglio geodetiche che non si incontrano, quindi non esistono parallele.
Nella figura sono rappresentati due meridiani perpendicolari
all'equatore e che si incontrano perpendicolarmente al polo Nord. Si
vede che la somma degli angoli interni del triangolo curvilineo ABN è
270°. In generale la somma degli angoli interni di un triangolo di questo
tipo è sempre maggiore di 180° e non è costante per tutti i triangoli.
Mentre nella geometria euclidea la somma degli angoli interni di un
triangolo è sempre 180°, nella geometria ellittica la somma degli angoli
interni del triangolo è variabile e dipende dalla grandezza del triangolo.

Un'altra caratteristica di questo tipo di geometria è che il rapporto
tra circonferenza e raggio è minore di PIGRECO.
Infatti, la circonferenza di diametro AB non ha centro in C ma in
N, ricorda che siamo sulla superficie della sfera, mentre C è posto
dentro la sfera. Poiché evidentemente l'arco AN è maggiore del
segmento AC, il rapporto tra la circoferenza AB e il suo raggio AN
è minore di PIGRECO.
Un modello intuitivo, dadatticamente utile per la geometria iperbolica o di Lobacevskj è un po' più complesso. In
particolare, non esiste un modello che rappresenti globalmente una geometria di questo tipo. Si può prendere
una superficie a forma di sella, o meglio la pseudosfera (vedi scheda sulla pseudosfera di Beltrami).
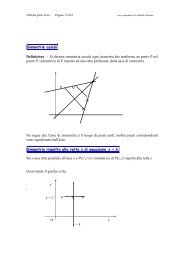
Per il punto P, esterno alla geodetica r, passano più geodetiche
(p1 e p2) che non incontrano la geodetica r e che quindi sono
parallele a r.
http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Non-Euclidean_geometry.html
P. Parrini, Fisica e geometria dall'Ottocento a oggi, Loescher, Torino, 1979
P. Freguglia, Fondamenti storici della geometria, Feltrinelli, Milano,1982
R. Bonola, La geometria non euclidea, esposizione storico critica del suo sviluppo, Zanichelli, Bologna, 1906
R Trudeau, La geometria non euclidea, Bollati Boringheri, Torino, 1991
Il triangolo curvilineo ABC su un pezzo di pseudosfera è il
corrispondente di un triangolo rettilineo del piano euclideo, perché
è composto da linee geodetiche. La somma degli angoli interni di
questo triangolo è minore di 180° e dipende dalla grandezza del
triangolo.

Note
Euclide Non si conoscono le date di nascita e di morte di questo grande matematico dell'antichità. Si pensa che fosse
di origine greca e che abbia studiato con Platone. Viene chiamato a insegnare ad Alessandria (Egitto) durante la dinastia
di Tolomeo I Sotere, che va dal 323 al 285 a.C. La sua opera più nota, gli Elementi, si fanno risalire all'anno 300 a.C.
L'opera si compone di tredici libri, nove dei quali di geometria, uno sulle proporzioni e tre di aritmetica. E' autore anche di
altre opere giudicate minori e riguardanti l'astronomia, la geodesia, l'ottica e la musica.
Si attribuiscono a Euclide due celebri battute. La prima è riferita da Proclo (V sec. d.C.). Un giorno Tolomeo gli chiede se
ci sia una strada più breve per imparare la geometria, invece che studiarla dagli Elementi. Euclide gli risponde che non
esiste una via regia per la geometria. La seconda è riferita da Stobeo (V sec. d.C.). Un giorno, un nuovo allievo di
Euclide chiede al maestro: "Cosa ci guadagno a imparare tutto questo?". Euclide prende delle monete e dice a un suo
aiutante: "Dagliele, dato che vuole guadagnare da ciò che impara".
Lobacevskij N. I. (1793-1856). Matematico russo, rettore dell'Università di Kazan (1827-46) è noto come il
matematico che ha fondato la prima delle geometrie non euclidee, conosciuta con il suo stesso nome. In questa
geometria la somma degli angoli interni di un triangolo è minore di due retti e per un punto esterno a una retta passa più
di una parallela alla retta data. Il primo scritto noto in cui ha esposto la sua teoria è del 1829 ed ha per titolo Sui principi
della geometria. Lobacevskij cercò anche di verificare sperimentalmente se la sua nuova geometria fosse empiricamente
valida a livello astronomico, senza però trovare conferme.
Bolyai J. (1802-1860). Ufficiale del genio ungherese è uno dei fondatori della geometria non euclidea iperbolica.
Probabilmente influenzato dal padre Farkas, amico di Gauss, pubblico un saggio sulla nuova geometria come Appendice
a un opera del padre. Tra i suoi può interessanti risultati la dimostrazione che, supposto non il vero il postulato di Euclide
sulle parallele, si può quadrare il circolo con riga e compasso.
Riemann B. (1826-1866). E' generalmente considerato uno dei creatori della matematica moderna: nei suoi pochi
scritti, infatti, lanciò diverse idee che furono il punto di partenza per nuovi campi di indagine nella matematica. Nel 1851
scrive i Fondamenti di una teoria generale delle funzioni di variabile complessa, da cui prenderà le mosse la moderna
fisica matematica. Altrettanto celebre la sua memoria del 1854 Sulle ipotesi che stanno alla base della geometria, da cui
prenderà l'avvio una concezione dello spazio e della geometria intesa in senso puramente matematico, svincolata
dall'indagine sullo spazio fisico. In questa memoria si trova uno studio della geometria, con strumenti tipici dell'analisi
matematica, più generale rispetto a quello euclideo, che comprende sia la geometria di Euclide sia quelle non euclidee.
Klein F. (1849-1925). Ha dato notevoli contributi in numerosi campi della matematica, cercando spesso una via
sintetica per collegare ricerche sviluppatesi in modo separato tra di loro. E' noto per aver dato una prova della coerenza
logica di quelle che lui definiva le "cosiddette geometrie non euclidee", dimostrando che sono casi particolari di una
geometria più generale, quella proiettiva. Nel suo Programma di Erlangen (1872) dà una struttura chiara, completa e
soprattutto unitaria delle diverse geometrie note al suo tempo. La base comune per tutte le ricerche geometriche è a suo
avviso nella nozione di gruppo di trasformazioni: ogni geometria studia le proprietà invarianti rispetto a un particolare
gruppo di trasformazioni che la contraddistingue.
Postulato Dal latino postulatum, da postulare, "chiedere". Proposizione posta alla base di una teoria, che si chiede
venga accettata senza dimostrazione.
V postulato o XI assioma di Euclide. Risulti postulato che, se una retta venendo a cadere su due rette forma gli angoli
interni e dalla stessa parte minori di due retti, le due rette prolungate illimitatamente verranno ad incontrarsi da quella
parte in cui sono gli angoli minori di due retti.
Enunciato delle parallele. E' una formulazione equivalente del V postulato di Euclide, essa afferma che per un punto
esterno a una retta data passa una e una sola parallela alla retta data.
Geodetica. Si chiama geodetica di una superficie una linea tracciata su di essa che ha la caratteristica di contenere il
percorso più breve per unire due punti della superficie senza uscire dalla superficie stessa. Nel piano la geodetica è la
retta, su una superficie sferica è un cerchio massimo, su un cilindro e un elica. Il vocabolo ha origine dal greco e significa
"dividere la terra".

Eugenio Beltrami (1835-1900)
Scheda: La pseudosfera di Beltrami
Verso la fine degli anni sessanta del XIX secolo, il dibattito sulle geometrie non
euclidee è particolarmente acceso.
Lobacevskj nel 1829 e Bolyai nel 1832 avevano scritto dei saggi in cui
dimostravano la possibilità di geometrie differenti da quella di Euclide, in
particolare geometrie nelle quali il famoso quinto postulato sulle parallele era
diverso da quello euclideo: per un punto esterno a una retta passa più di una
parallela alla retta data.
Le ricerche di questi matematici erano rimaste pressoché ignorate fino a che con
la morte di Gauss (1855) e la pubblicazione del suo epistolario si viene a sapere
che anche il sommo Gauss aveva avuto la stessa idea. L'interesse per questo
problema fa emergere una memoria che Riemann, allievo di Gauss, aveva
scritto nel 1854 ed era rimasta inedita: Sulle ipotesi che stanno a fondamento
della geometria. La memoria pubblicata nel 1867 forniva un nuovo modo di
intendere la geometria. Da un lato presentava la geometria come un caso
particolare di un nuovo concetto matematico, la varietà pluridimensionale;
dall'altro presentava un secondo caso di geometria non euclidea, la geometria
ellittica, nella quale non esistono rette parallele.
Incoraggiato dalle pubblicazioni di personaggi così celebri, il giovane matematico
italiano Eugenio Beltrami si decide a dare alle stampe un suo manoscritto
redatto qualche anno prima e messo da parte per paura delle aspre critiche che
coinvolgevano chi si occupava di geometrie 'astrali' o 'da manicomio'. Il suo
Saggio di interpretazione della geometria non euclidea segna un punto di svolta
nella ricerca geometrica su questo millenario problema.
Beltrami aveva trovato un 'substrato reale' per la geometria di Lobacevskj, ossia
aveva trovato all'interno della geometria euclidea, una superficie di rotazione, la
pseudosfera, che poteva essere interpretata come un modello euclideo di
geometria non euclidea. In questo modo dimostrava che la geometria di
Lobacevskj ha lo stesso diritto logico-matematico della classica geometria di
Euclide. Alla superficie aveva dato il nome di pseudosfera perché ha curvatura
costante come una sfera ma di segno negativo.
Per capire come avviene questa 'traduzione' occorre introdurre la nozione di
geodetica. Nel piano il percorso più breve che unisce due punti si trova sulla
retta passante per i due punti. Estendendo questo concetto alle superfici, il
percorso più breve che unisce due punti della superficie si trova su di una linea,
generalmente curva, detta geodetica. Per esempio, dovendosi muovere sulla
superficie di una sfera, il percorso più breve non è quello rettilineo, perché non
esistono percorsi di questo tipo, ma è l'arco di cerchio massimo, che in questo
caso è una geodetica.
La 'traduzione' si ottiene interpretando la superficie pseudosferica come piano di
Lobacevski, le rette di questo piano sono le geodetiche della superficie.

Lobacevski, le rette di questo piano sono le geodetiche della superficie.
Geodetiche sulla sfera traduzione
Un disegno nel piano del modello di
Beltrami. La regione C colorata è il
modello. Per il punto P esterno alla retta r
passano almeno due rette, t e t', che non
incontrano la retta r.
L'immagine è presa da
• superficie pseudosferica
• punto della superficie
• geodetica
• arco di geodetica
• due punti determinano una
geodetica
• per un punto esterno a una
geodetica passano infinite
geodetiche che non si
incontrano con quella data
• regione di piano non euclideo
• punto del piano
• retta del piano
• segmento del piano
• due punti determinano una retta
del piano
• per un punto esterno a una retta
passano infinite rette parallele alla
retta data
Tuttavia, alcuni matematici hanno perplessità circa la validità del ragionamento
di Beltrami. Il punto più debole dell'argomentazione sta nel fatto che il modello
ha valore locale e non può rappresentare globalmente la geometria non
euclidea. Infatti, tra le infinite forme che una superficie pseudosferica può
assumere si conosce l'espressione analitica solo di qualche caso particolare.
Beltrami l'aveva ottenuta dalla rotazione di una curva studiata da F. Minding, la
trattrice. Questa curva ha il difetto di avere un punto cuspidale, che ruotando dà
origine a un cerchio di punti singolari della superficie: la superficie ottenuta dalla
rotazione della trattrice quindi non è regolare e non può rappresentare
interamente il piano non euclideo.
Il problema è allora se tra tutte le superfici, delle quali non si conosce
l'espressione analitica, ne esiste almeno una che sia regolare. Beltrami ne è
convinto ma non riesce a provarlo.
"Ho avuto un'idea bizzarra", scrive Beltrami a un suo amico matematico
francese, Hoüel, "ho voluto tentare di costruire materialmente la superficie
pseudosferica sulla quale si realizzano i teoremi della geometria non euclidea". Il
modello materiale costruito in cartone aveva il diametro di 1,04 m; oggi è
custodito presso il dipartimento di matematica dell'Università di Pavia.
Soltanto nel 1901 Hilbert dimostra rigorosamente che il modello descritto da
Beltrami ha un valore esclusivamente locale e non può essere accettato come
prova matematica. Nel frattempo però altre dimostrazioni erano state già
ottenute.
Il modello di Beltrami, pur non essendo un modello rigoroso, ha avuto un grande
ruolo storico perché ha fornito la chiave per interpretare le nuove geometrie non
euclidee.
Antonio Bernardo
Beltrami E., Saggio di interpretazione della geometria non-euclidea, in "Giornale
di matematiche", (6) 1868, pp. 284-312.
Beltrami E., Sulla superficie di rotazione che serve di tipo alle superficie

The MacTutor History of Mathematics
archive
pseudosferiche, in "Giornale di matematiche", (10) 1872, pp. 147-159.
Beltrami E. Opere matematiche, Hoepli, Milano, 1902.
Bonola R., Il modello di Beltrami di superficie a curvatura costante negativa, in
"Bollettino di bibliografia e storia delle scienze matematiche, 1906, pp. 33-38.
Capelo A.C., Ferrari M., La cuffia di Beltrami: storia e descrizione, in "Bollettino
di storia delle scienze matematiche", 1982, pp. 233-247.
Nella rete
http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Beltrami.html
http://www.britannica.com/bcom/eb/article/2/0,5716,15522+1,00.html
http://chronomath.irem.univ-mrs.fr/chronomath/Beltrami.html
http://chronomath.irem.univ-mrs.fr/chronomath/DisqueBeltrami.html
http://chronomath.irem.univ-mrs.fr/chronomath/tractrice.html