Lista 5 - CEUNES

5a LISTA DE EXERCÍCIOS DE CÁLCULO I
1) Defina antiderivada e integral indefinida. Explicite a diferença entre os dois conceitos.
10
2) Estime x 3 dx por somas de Riemann, particionando [0,10] em 5 subintervalos de mesmo comprimento
0
e tomando os pontos ck (os pontos dos subintervalos onde a função é aplicada) como
a) as extremidades esquerdas de cada subintervalo c1 = 0, c2 = 2,..., c5 = 8.
b) os pontos médios dos subintervalos, isto é, c1 = 1,..., c5 = 9.
c) as extremidades direitas de cada subintervalo.
Interprete geometricamente em termos de áreas e compare os resultados com o valor exato da integral, que é
2500.
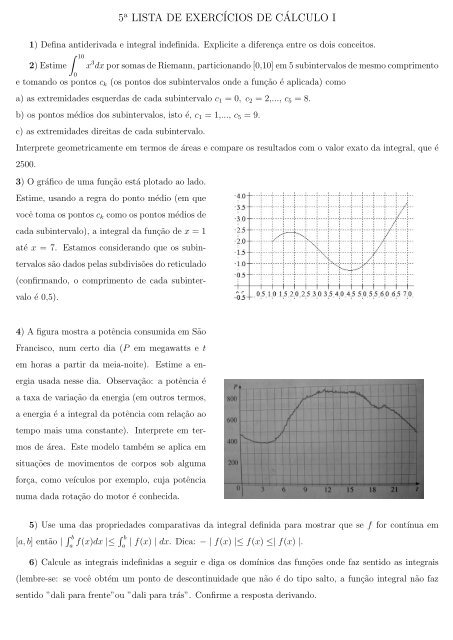
3) O gráfico de uma função está plotado ao lado.
Estime, usando a regra do ponto médio (em que
você toma os pontos ck como os pontos médios de
cada subintervalo), a integral da função de x = 1
até x = 7. Estamos considerando que os subin-
tervalos são dados pelas subdivisões do reticulado
(confirmando, o comprimento de cada subinter-
valo é 0,5).
4) A figura mostra a potência consumida em São
Francisco, num certo dia (P em megawatts e t
em horas a partir da meia-noite). Estime a en-
ergia usada nesse dia. Observação: a potência é
a taxa de variação da energia (em outros termos,
a energia é a integral da potência com relação ao
tempo mais uma constante). Interprete em ter-
mos de área. Este modelo também se aplica em
situações de movimentos de corpos sob alguma
força, como veículos por exemplo, cuja potência
numa dada rotação do motor é conhecida.
5) Use uma das propriedades comparativas da integral definida para mostrar que se f for contínua em
[a, b] então | b
a f(x)dx |≤ b
| f(x) | dx. Dica: − | f(x) |≤ f(x) ≤| f(x) |.
a
6) Calcule as integrais indefinidas a seguir e diga os domínios das funções onde faz sentido as integrais
(lembre-se: se você obtém um ponto de descontinuidade que não é do tipo salto, a função integral não faz
sentido ”dali para frente”ou ”dali para trás”. Confirme a resposta derivando.

√2x
x
a) + 1 + e dx
b) t 3 · cos (t 4 + 2)dt
c)
y
dy
1 − 4y2
d)
[sec
2
−1y] 3
| y | y2 − 1 dy
e) tg y − 4
dy
y
1
f) + sen2 (x − 1) · cos(x − 1) dx
g)
2
e x
− dx
x2 h) x 2 + 2x − tg(e x ) · e x dx
7) Nas 8 integrais do exercício anterior, calcule as integrais definidas com limites de -10 a 10. No caso das
integrais que não existem, obtenha outros limites de integração de modo que a integral exista. Quanto maior
for os limites de integração que voçê obtiver, melhor é.
8) Nos exercícios seguintes derive as funções com relação a x usando o teorema fundamental do Cálculo.
3
t
a)
−x
2 + 5t − 1
t2 x4 dt b) cos (t
+ 8
−x
3 x
)dt c) sec(t) · tg(t)dt
π
6
Dica para o ítem b: particione o intervalo de integração em duas partes, use a regra da soma para derivadas
e o teorema fundamental para cada uma das integrais.
Comentário sobre o ítem c: dá para integrar direto, e depois calcular a derivada; verifique que dá o mesmo
resultado, mas com teorema fundamental dá menos trabalho... além disso, tente usar a mesma estratégia
para os ítens a) e b); calcular a integral é bem mais complicado (em certos casos é impossível).
5
(2r − 1) cos
9) Calcule
−2
3(2r − 1) 2 + 6
dr pelo método tradicional (em que você volta à variável inicial)
3(2r − 1) 2 + 6
e também pela regra da substituição. Só leia a dica seguinte depois de tentar fazer sem ela.
Dica: primeiro faça u = 3(2r − 1) 2 + 6 e depois v = √ u.
a)
10) Calcule as integrais a seguir, no caso de estas existirem. Se não existir explique porque.
√ π
2
0
(x · sec(x 2 ) − √ 4 + 3x)dx b)
√ π
4
0
(x · sec(x 2 ) − √ 4 + 3x)dx
9
3
11 Seja f uma função contínua e f(x)dx = 4. Ache x (f(x 2 ))dx e justifique sua resposta. (dica:
0
regra da substituição para integrais definidas).
b
−a
12 Se f é contínua em R mostre que f(−x)dx = f(x)dx. Dica: novamente substituição.
a
b
b+2
13 Sendo f contínua em toda a reta, mostre que f(x + 2)dx = f(x)dx. Para o caso onde f(x)
é sempre positivo, faça uma figura e interprete este resultado como uma igualdade de áreas. Dica para a
primeira parte: substituição. Dica para a segunda parte: como fica o gráfico de f(x) a partir do gráfico de
f(x + 2)?
a
14) Calcule as integrais definidas a seguir, caso estas existam; se não existir explique por que. Diga se
existe algum ponto no intervalo de integração onde é preciso ”quebrar” a integral. Faça o cálculo usando a
regra da substituição e também o outro método (em que você volta até a variável inicial e então substitui os
limites de integração):
e4 dx
a)
x √ ln x
e
−b
0
a+2
−3
x + 1
b)
−2π x2 3
x + 1
dx c)
+ 2x −2π x2 + 2x dx

6
−π
0
15) a) Se f é par (isto é, f(−x) = f(x)) e integrável
f(x)dx?
b) O mesmo exercício que o anterior, mas supondo f ímpar, isto é, f(−x) = −f(x).
16) Calcule
5
2
1
2
−π
6
f(x)dx = −3 e f(x)dx = 4, qual o valor de
3x − 6
3x2 dx. O integrando é uma função contínua no intervalo
− 3x − 6
π
1 5
, ?
2 2
17) Calcule os valores médios das funções seguintes nos intervalos especificados. O que o teorema do valor
médio para integrais garante nesses casos. Quando factível, tente achar c em [a, b] tal que f(c) é igual ao valor
médio encontrado.
1
a) f(x) =
| x | √ x2 − 1 + 2 no intervalo [−√2, 2].
b) f(x) = x2 − 3x + 2 no intervalo [−1, 4].
18) Meteorologistas
modelaram
a função temperatura de uma cidade com a função
2π
f(t) = 37 sen (t − 101) + 28 para um ano de 365 dias (0 ≤ t ≤ 365), onde a temperatura é dada
365
em graus Celsius ( oC) e o tempo em dias. Mostre que a temperatura média da cidade ao longo de um ano,
ou seja, o valor médio da função no intervalo de tempo especificado, é 28 o C. Dica: se a + b = 2 π então cos a
= cos b; use este fato no meio dos cálculos.
19) Calcule a área das regiões indicadas a seguir e faça um esboço da região no plano cartesiano:
a) a região limitada pelas curvas y = sen(x), y = ex , x = 0 e x = π
e esboçe a região no plano cartesiano.
2
b) a região limitada pelas curvas x = 1 − y2 e x = y2 − 1.
c) a região limitada pelas curvas y = sec2x, y = tg2x, x = − π π
e x = . Dica: usando uma relação
4 4
trigonométrica fica ainda mais fácil, inclusive de enxergar a região.
1
d) a região limitada pelas curvas y = √
1 − x2 y = 2 − 2x2 . Observação: é difícil achar a interseção entre
as curvas y =
1
√ 1 − x 2 e y = 2 − 2x2 (”cai”num problema de achar uma raíz da equação do sexto grau).
Pelo menos mostre como chegar nessa equação. Chame a raíz desejada (uma das raízes complexas daquele
polinômio) de α. Pode dar a área pedida em função de α.
20) Encontre os valores de c tais que a área da região limitada pelas parábolas y = x 2 − c 2 e y = c 2 − x 2
seja 576. Faça um esboço da região para c = 1.
Bibliografia
1. STEWART, James. Cálculo. 4 a ed. São Paulo: Pioneira Thomson Learning, 2006.
2. THOMAS JR., George B. et al. Cálculo. 10 a ed. São Paulo: Pearson Addison Wesley, 2002.