Ficha de revisão nº

ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS
10º ANO DE MATEMÁTICA – A
Ficha de revisão nº 12
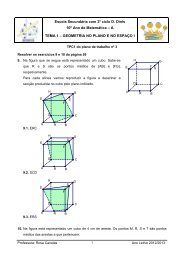
1. Na figura está representada, em referencial o.n. Oxyz, uma caixa cilíndrica construída num material de
espessura desprezável.
A caixa contém duas bolas encostadas uma à outra e às bases
da caixa cilíndrica.
• O cilindro tem uma das bases no plano xOz.
• O centro dessa base é o ponto de coordenadas ( 3,0,3 )
• A outra base está contida no plano de equação y = 12
• As bolas são esferas de raio igual a 3.
• Os diâmetros das esferas e das bases do cilindro são iguais
1.1. Justifique que a superfície esférica correspondente à bola mais afastada do plano xOz tem centro
no ponto ( 3,9,3 )
1.2. Escreva uma equação da superfície esférica correspondente à bola mais afastada do plano xOz.
1.3. Verifique que o ponto ( 1, 8,1 ) pertence à superfície esférica superfície esférica correspondente à
bola mais afastada do plano xOz.
1.4. Considere agora a caixa vazia. Seccionou-se a caixa pelo plano de equação z = 4. Supondo que
a unidade do referencial é o centímetro, determine o perímetro da secção obtida.
1.5. Escreva uma equação do plano paralelo a xOz e que passa no centro da esfera tangente ao plano
xOz.
1.6. Escreva uma equação vectorial da recta definida pelos centros das duas esferas.
1.7. Indique as coordenadas do ponto de intersecção das duas esferas.
2. Na entrada dum túnel existe um arco assente em dois pilares de igual altura. A altura do arco a x metros
de distância do pilar da esquerda é dada, em metros, por
h( x) =− 1 ( x− 4) 2
+ 7.
8
2.1. Mostre que h0 ( ) = 5 e interprete o resultado.
2.2. Indique a altura máxima do arco.
2.3. Determine a largura do túnel.
2.4. A que distância do pilar da esquerda a altura do arco é superior a 6,5 metros?
Professora Rosa Canelas 1 Ano lectivo 2006/2007

ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS
10º ANO DE MATEMÁTICA – A
Ficha de revisão nº 12 – Proposta de resolução
1. Na figura está representada, em referencial o.n. Oxyz, uma caixa cilíndrica construída num
material de espessura desprezável.
A caixa contém duas bolas encostadas uma à outra e às bases
da caixa cilíndrica.
• O cilindro tem uma das bases no plano xOz.
• O centro dessa base é o ponto de coordenadas ( 3,0,3 )
• A outra base está contida no plano de equação y = 12
• As bolas são esferas de raio igual a 3.
• Os diâmetros das esferas e das bases do cilindro são iguais
1.1. A superfície esférica correspondente à bola mais afastada do plano xOz tem centro no
ponto ( 3,9,3 ) porque dista 3 do plano yOz por ser 3 o raio de cada esfera, dista 9 do
plano xOz por essa distância ser o diâmetro da outra esfera mais o raio desta e finalmente
dista 3 do plano xOy por ser 3 o raio da esfera.
1.2. Uma equação da superfície esférica correspondente à bola mais afastada do plano xOz é
( ) ( ) ( )
2 2 2
x− 3 + y− 9 + z− 3 = 9
1.3. Para verificarmos se o ponto ( 1,8,1 ) pertence à superfície esférica correspondente à bola
mais afastada do plano xOz vamos ver se as suas coordenadas verificam a equação da
2 2 2
1− 3 + 8− 9 + 1− 3 = 9⇔ 4+ 1+ 4= 9⇔ 9=
9
alínea anterior: ( ) ( ) ( )
1.4. Consideremos agora a caixa vazia. Seccionou-se a caixa
pelo plano de equação z = 4 . Supondo que a unidade do
referencial é o centímetro, determinemos o perímetro da
secção obtida. Temos de começar por ver que a secção é
um rectângulo de comprimento igual a 12 (altura do
3
1
x
3
cilindro) falta-nos encontrar a largura do rectângulo que
podemos calcular a partir da vista em verdadeira grandeza
desse segmento que de acordo com a figura é 2x. Vamos
calcular x utilizando o Teorema de Pitágoras:
2 2 2 2
x + 1 = 3 ⇔ x = 8⇔ x = 2 2 . A largura do rectângulo mede 4 2 e o perímetro será
P = 12+ 12+ 4 2 + 4 2 ⇔ P= 24+
8 2
Professora Rosa Canelas 2 Ano lectivo 2006/2007

1.5. Uma equação do plano paralelo a xOz e que passa no centro da esfera tangente ao plano
xOz é y = 3 .
1.6. Para escrever uma equação vectorial da recta definida pelos centros das duas esferas
precisamos de um ponto e de um vector. Um ponto pode ser (3,9,3) e um vector pode ser
o vector que tem origem no centro da esfera tangente a xOz e extremidade no centro da
outra esfera. Esse vector tem coordenadas (0,6,0).
Uma equação da recta é ( x, y,z) = ( 3,9,3 ) + k ( 0,6,0 ), k ∈
1.7. As coordenadas do ponto de intersecção das duas esferas são ( 3,6,3 )
2. Na entrada dum túnel existe um arco assente em dois pilares de igual
altura. A altura do arco a x metros de distância do pilar da esquerda é
dada, em metros, por h( x) =− 1 ( x− 4) 2
+ 7.
8
h0 =− 1 0− 4 + 7= 5o que significa que cada pilar mede 5 metros.
8
2.1. ( ) ( ) 2
2.2. A altura máxima do arco é dada pela ordenada do vértice da parábola que representa a
função e que neste caso é 7 metros porque V( 4,7 ) .
2.3. O túnel tem 8 metros de largura pois o vértice pertence ao eixo de simetria da figura e se
dista 4m do primeiro pilar também dista 4 metros do segundo pilar o que nos leva a
concluir que a distância entre os dois pilares é 8 m.
2.4. Para sabermos a que distância do pilar da esquerda a altura do arco é superior a 6,5
metros, vamos utilizar a calculadora
Concluímos assim que a altura do arco é superior a 6,5 metros desde o ponto do arco que
dista 2 metros do pilar da esquerda até ao ponto do arco que dista 6 metros do pilar da
esquerda.
Podíamos resolver analiticamente resolvendo a inequação:
1
( x 4 ) 2 7 6,5 x
2 8x 16 56 52 0 x
2
− − + > ⇔ − + − + − > ⇔ − + 8x − 12 > 0
8
Cálculo dos zeros:
2 − 8± 64−48 − 8±
4
− x + 8x− 12= 0⇔ x = ⇔ x = ⇔ x = 6∨ x = 2
−2 −2
Atendendo agora a que a parábola tem a concavidade voltada para baixo
positivo quando x∈ ] 2,6[
.
2
− x + 8x− 12 é
Professora Rosa Canelas 3 Ano lectivo 2006/2007