22. parametry geometryczne figur płaskich

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 1
22.
PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH
22.1. DEFINICJE
Rozdział 22. dotyczy figur płaskich o równomiernym rozkładzie masy
(ρ = const). Rozważane figury reprezentują zazwyczaj przekroje prętów. Dlatego zamiast określenia „figura
płaska” stosuje się również określenie „przekrój”.
Definicje poszczególnych parametrów geometrycznych figur płaskich wymagają wprowadzenia prostokątnego
układu osi współrzędnych x, y (rys. 22.1).
Pole przekroju
Momenty statyczne przekroju:
− względem osi x
− względem osi y
Momenty bezwładności:
− względem osi x
− względem osi y
− odśrodkowy (dewiacyjny)
Rys. 22.1 Rys. 22.2
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
A= ∫
dA>
0 [m 2 ]. (22.1)
A
Sx
=
∫
ydA [ m 3 ],
A
Sy
=
3
∫
xdA [ m ].
A
Jx
=
∫
y 2 dA>
0 [ m 4 ],
A
Jy
=
∫
x 2 dA>
0 [ m 4 ],
A
Jxy
=
∫
x 2 dA [ m 4 ].
A
(22.2a)
(22.2b)
(22.3a)
(22.3b)
(22.3c)
Z podanych wyżej wzorów definicyjnych wynika, że momenty statyczne mierzymy w jednostkach
długości do potęgi trzeciej (np. [m 3 ], [cm 3 ]). Mogą one przyjmować wartości dodatnie lub ujemne. Momenty
bezwładności mierzymy w jednostkach długości do potęgi czwartej (np. [m 4 ], [cm 4 ]). Osiowe
momenty bezwładności przybierają zawsze wartości dodatnie i są pewną miarą rozproszenia pola figury
względem danej osi. Im rozproszenie jest większe, tym osiowy moment bezwładności jest większy. Moment
dewiacyjny może być zarówno dodatni, jak i ujemny, a jego wartość bezwzględna jest miarą asyme-
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 2
trii figury względem przyjętego układu współrzędnych. Łatwo zauważyć, że jeśli choć jedna z osi układu
jest osią symetrii figury, to moment dewiacyjny względem tego układu jest równy zeru (por. rys. 22.2).
Wynika to stąd, że iloczyny xydA w odpowiadających sobie punktach wzajemnie się znoszą.
22.2. OSIE ŚRODKOWE, ŚRODEK CIĘŻKOŚCI
Oś środkowa to taka oś, względem której moment statyczny jest równy zeru. Środek ciężkości (SC) to
punkt przecięcia osi środkowych.
Rys. 22.3 Rys. 22.4
Jeśli osie x0 i y0
są osiami środkowymi, to
(a) Sx
= y dA y yc
dA
0 ∫ 0 =
∫
( − ) = 0,
A A
(b) Sy
= x dA x xc
dA
0 0 = ( − ) = 0.
∫ ∫
A A
Po rozpisaniu zależności (a) i (b) otrzymujemy:
Sx = ydA− yc dA= Sx − yc⋅ A=
0,
0
A
A
Sy = xdA− xc dA= Sy −xc⋅ A=
0,
0
∫
∫
A
∫
∫
A
skąd wyznaczamy współrzędne środka ciężkości xc
i yc:
S y
S
xc
= , y x
c = . (22.4)
A
A
Jeśli znamy położenie środka ciężkości i pole figury, to momenty statyczne tej figury względem osi x, y
leżących w odległościach xc
i yc
obliczamy wprost z równań (22.4):
Sx = A⋅ yc, Sy = A⋅xc.
Jeśli figura składa się z n części o znanych polach A i oraz współrzędnych środków ciężkości
xi
i yi
( i = 12 , ,..., n)
, to (por. rys. 22.4):
n n
n n
Sx = ∑Sx = Ai yi
Sy Sy Ai x
i ∑ ⋅ ; = ∑ = i ∑ ⋅ i .
(22.5)
i= 1 i=
1
i=
1 i=
1
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 3
n
n
∑ Ax i i ∑ Ay i i
Sy
S
x i
c = = = 1 ; y x i
A n c = = = 1 .
A n
∑ Ai
∑ Ai
(22.6)
i=
1
i=
1
22.3. MOMENTY BEZWŁADNOŚCI PRZY PRZESUNIĘCIU
I OBROCIE UKŁADU OSI WSPÓŁRZĘDNYCH.
KIERUNKI I WARTOŚCI GŁÓWNE
Założymy, że znamy wartości momentów bezwładności J x' , J y' , J x'y' odniesione do układu osi x' i y'.
Dokonajmy przesunięcia równoległego układu osi z położenia x', y' do nowego położenia x, y. Pytamy
teraz, jakie wartości przyjmą momenty bezwładności J x , J y , J xy odniesione do układu osi x, y, jeśli współrzędne
przesunięcia względnego obu układów wynoszą x p i y p (rys. 22.5). Przesunięcie układów opisują
równania:
(a)
⎧⎪
x = x' + xp
,
⎨
⎩⎪ y = y' + yp.
Po podstawieniu tych zależności do wzorów definicyjnych (22.3) otrzymujemy:
(b)
⎧
⎪ 2 2 2 2
Jx = y dA = y + yp dA = y dA + yp y dA + yp
dA
⎪ ∫ ∫(' )
∫
' 2
∫
'
∫
,
⎪ A A
A
A A
⎪ 2 2 2 2
⎨Jy =
∫
x dA =
∫(' x + xp) dA =
∫
x' dA + 2xp∫
x' dA + xp∫dA,
⎪ A A
A
A A
⎪
⎪Jxy = xydA= (' x+ xp)(' ⋅ y+ yp) dA= xydA '' + xp ydA ' + yp
xdA ' + xpyp
dA.
⎪ ∫ ∫ ∫ ∫ ∫ ∫
⎩ A A
A
A A
A
Rys. 22.5 Rys. 22.6
Prawe strony równań (b) można przedstawić za pomocą parametrów geometrycznych figury związanych
z układem x', y' wykorzystując wzory (22.1), (22.2)
i (22.3):
⎧
2
Jx = Jx'
+ 2yp⋅ Sx'
+ yp⋅A,
⎪
2
(c)
⎨Jy = Jy'
+ 2xp⋅ Sy'
+ xp⋅A,
⎪
Jxy = Jx y + xpSx + yp ⋅ Sy + xp ⋅yp
⋅A
⎩
⎪ ' ' ' ' .
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 4
Jeśli układ osi x', y' jest układem osi środkowych ( x'= x 0 , y'= y 0 , xp
= xc, yp
= yc), to wzory (c)
znacznie się uproszczą. Dla osi środkowych momenty statyczne Sx' = Sx = 0 i Sy S
o ' = y = 0,
a równania
(c) przyjmą
o
postać:
2
Jx = Jx + y A ⎫
0 c ,
2 ⎪
Jy = Jy0
+ xc
A,
⎬
⎪
Jxy = Jx0y0
+ xc yc
A.
⎭⎪
(22.7)
Są to tzw. wzory Steinera, bardzo użyteczne w obliczeniach.
Rozważymy teraz, jak zmieniają się momenty bezwładności przy obrocie układu osi współrzędnych.
Przyjmiemy, że znane są wartości J x , J y , J xy w układzie osi x, y. Poszukujemy J x' , J y' , i J x'y' w układzie osi
x', y' obróconym o kąt ϕ względem układu x y (rys. 22.6). Współrzędne punktów obu układów są powiązane
wzorami transformacyjnymi:
⎧x' = xcosϕ
+ ysin ϕ,
(d)
⎨
⎩y' =− xsinϕ
+ ycos ϕ.
W celu wyprowadzenia poszukiwanych zależności skorzystamy ze wzoru na zamianę zmiennych w całce
podwójnej:
∫
f ( x', y') dA' = f x'( x, y), y'( x, y) J⋅dA,
(e) [ ]
gdzie jakobian
A
J =
∂x'
∂x
∂y'
∂x
∂x'
∂y
∂y'
∂y
∫
A
cosϕ
sinϕ
= = 1 .
− sinϕ
cosϕ
Po podstawieniu wzorów transformacyjnych (d) do wzorów definicyjnych otrzymujemy:
(f)
∫
∫
⎧ 2 2
Jx'
= y' dA' = ( − x sinϕ
+ y cos ϕ)
dA =
⎪
⎪ A'
A
⎪ 2 2 2 2
⎪ = sin ϕ∫x dA− 2 sinϕcosϕ∫
xydA+
cos ϕ∫
y dA,
⎪
A
A
A
⎪
2 2
⎪ J y'
=
∫
x' dA' =
∫
( x cosϕ
+ y sin ϕ)
dA =
⎪ A'
A
⎨
2 2 2 2
⎪ = cos ϕ∫x dA+ 2sinϕcosϕ∫
xydA+
sin ϕ∫
y dA,
⎪
A
A
A
⎪
⎪
2
Jxy''
=
∫
x' y' dA' =
∫
( xcosϕ + ysin ϕ)( − xsinϕ + ycos ϕ)
dA=
⎪
⎪ A'
A
⎪
2 2 2 2
⎪
=− sinϕcosϕ∫x dA + sinϕcos ϕ∫
y dA + (cos ϕ −sin ϕ∫xydA.
⎩⎪
A
A
A
Prawe strony równań (f) można wyrazić za pomocą momentów bezwładności związanych z układem osi
x, y. Wygodnie też będzie wprowadzić funkcję trygonometryczne kąta 2ϕ:
2 1
2
2 1
2
sin ϕ = ( 1− cos 2ϕ); cos ϕ = ( 1+ cos 2ϕ); 2sinϕcosϕ = sin 2ϕ.
Ostatecznie poszukiwane wzory transformacyjne dla momentów bezwładności przy obrocie układu przyjmują
postać:
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 5
Jx + Jy Jx − Jy
⎫
Jx'
= + ⋅cos2ϕ
− Jxy
sin 2ϕ,
⎪
2 2
⎪
Jx + Jy Jx − Jy
⎪
J y'
= − ⋅ cos2ϕ
+ Jxy
sin 2ϕ,
⎬
2 2
⎪
Jx
− Jy
⎪
Jxy
' ' = sin 2ϕ
+ Jxy
cos 2ϕ.
⎪
2
⎭
(22.8)
Rzut oka na wzory (22.8) pozwala stwierdzić, że po obrocie układu suma osiowych momentów bezwładności
nie ulega zmianie. Suma ta określa tzw. biegunowy moment bezwładności J b . Moment ten jest
więc niezmiennikiem:
Jb =
∫ ( 2 2
x + y ) dA= Jx + Jy = Jx' + Jy'
= const. (22.9)
A
Szczegółowa analiza wzoru (22.8) prowadzi do wniosku, że niezmiennikiem jest również wyrażenie:
2 2
I3
= JxJy − Jxy = Jx' ⋅Jy' − Jx' y' = const .
(22.10)
W punkcie 22.1 zwróciliśmy uwagę na to, że jeśli jedna z osi układu jest osią symetrii figury, to moment
dewiacyjny w tym układzie jest równy zeru. Powstaje pytanie, czy dla dowolnego niesymetrycznego
przekroju jest również taki układ osi, w którym znika moment dewiacyjny. Wymaganie, by J x'y' = 0,
stosownie do wzoru (22.8) 3 , nakłada na kąt ϕ = ϕ 0 warunek:
Jx
− Jy
(g)
⋅ sin2ϕ0 + Jxy
cos 2ϕ
0 = 0,
2
skąd
2Jxy
tg2ϕ 0 =− . (22.11)
Jx
− Jy
Zwróćmy uwagę, że do identycznego warunku z warunkiem (g) dochodzimy, poszukując ekstremalnych
wartości osiowych momentów bezwładności jako funkcji kąta ϕ:
dJy' dJ J J
x x − y
=− ' = 2 ⋅ ⋅ sin2ϕ
+ 2⋅ Jxy
cos 2ϕ
= 0 .
dϕ
dϕ
2
Z powyższych rozważań wnioskujemy, że jest pewien wyróżniony układ osi współrzędnych, określony
kątem ϕ 0 , dla którego osiowe momenty bezwładności osiągają wartości ekstremalne, a moment dewiacyjny
znika. Taki układ osi nazywamy układem głównych osi bezwładności (I, II), a momenty osiowe
w tym układzie − głównymi momentami bezwładności. Wartości głównych momentów bezwładności
obliczamy po wstawieniu kąta ϕ 0 z równania (22.11) do równań (22.8) 1 i (22.8) 2 :
2 ⎫
Jx + Jy ⎛ Jx − Jy⎞
2
Jmax
= J = + ⎜ ⎟ + Jxy
, ⎪
I
2 ⎝ 2 ⎠
⎪
⎬ ... (22.12)
2
Jx + Jy ⎛ Jx − Jy⎞
⎪
2
Jmin
= JII
= − ⎜ ⎟ + Jxy
. ⎪
2 ⎝ 2 ⎠
⎭⎪
Położenie osi I związanej z momentem J I określa się następująco:
− jeśli J x > J y , to ϕ 0 jest kątem pomiędzy osią x a osią I,
− jeśli J x < J y , to ϕ 0 jest kątem pomiędzy osią y a osią I.
Najczęściej obliczenia wykonujemy w układzie osi środkowych x 0 , y 0 . Wówczas osie I i II nazywamy
głównymi środkowymi osiami bezwładności, a momenty J I i J II − głównymi środkowymi momentami
bezwładności.
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 6
Uważny czytelnik stwierdzi uderzającą analogię między wzorami (22.8)÷(22.11) a zależnościami występującymi
w analizie płaskiego stanu naprężenia (p. 1.8). Jeśli we wzorach (22.8) przyjmiemy, że:
Jx = σx , Jy = σy , Jxy = τxy , Jx' = σx' , Jy' = σy' , Jx' y' = τx' y' ,
to otrzymamy zależności identyczne z wzorami transformacyjnymi (1.33) dla płaskiego stanu naprężenia.
Analogia ta wynika stąd, że momenty bezwładności tworzą płaski tensor drugiego rzędu. Wyjaśnienie
tensorowego charakteru momentów bezwładności zamieszczono w p. 22.4.
Wobec powyższego koło Mohra, omówione szczegółowo w rozdziale 1. (p. 1.8), jest również ilustracją
graficzną wzorów transformacyjnych (22.8). Dla jasności trzeba też dodać, że konstrukcję koła wykonuje
się, przyjmując że J yx = −J xy ! Ciekawostką jest, że Mohr w 1887 roku obmyślił konstrukcję koła
właśnie dla momentów bezwładności.
22.4. PARAMETRY GEOMETRYCZNE PRZEKROJU
JAKO WIELKOŚCI TENSOROWE
Momenty statyczne nazywają się często momentami pierwszego rzędu (stopnia), a momenty bezwładności
− momentami rzędu rzędu (stopnia). Określenia te wynikają z potęg, w których występują współrzędne
x, y we wzorach (22.2) i (22.3). Pole przekroju można by nazwać momentem rzędu zero. Nadmieniamy
o tym nieprzypadkowo, gdyż pole przekroju, momenty statyczne i momenty bezwładności mają
własności tensorów odpowiednio rzędu zerowego, pierwszego i drugiego. Pole przekroju jest skalarem,
momenty statyczne S x i S y są współrzędnymi wektora, a momenty bezwładności J x , J y , J xy − współrzędnymi
tensora dwuwymiarowego.
Dla potwierdzenia powyższych uwag wyprowadzimy prawa transformacji momentów statycznych i
momentów bezwładności dla obrotu układu współrzędnych. Przyjmiemy najpierw następujące oznaczenia:
⎧x1 = x, x2 = y; x1'
= x', x2'
= y';
(a)
⎨
⎩
M1 = Sy, M2 = Sx; B11 = Jy, B22 = Jx,
B12 = B21
= Jxy
Wówczas wzory definicyjne (22.2) i (22.3) można zapisać następująco:
(b) Mα
=
∫
xαdA,
A
(c) Bαβ = xα xβdA,( αβ , = 12 , ),
∫
A
a wzory transformacyjne współrzędnych punktów w konwencji sumacyjnej określają znane zależności
(por. rozdz. 1.):
(d) xγ'
= xα ⋅ aαγ'
lub
(e) xδ' = xβ ⋅ aβδ' ( α, β = 1, 2; γ ', δ ' = 1', 2 ').
W układzie osi obróconych, stosownie do definicji (b) i (c) oraz wzorów (d) i (e), możemy napisać:
Mγ' = ∫
xγ' dA' = ∫
xα ⋅ aαγ' dA = aαγ'
∫ xαdA,
A'
A
A
Bγ ' δ ' =
∫
xγ ' ⋅ xδ ' dA' =
∫
xα aαγ ' ⋅ xβaβδ ' dA= aαγ ' aβδ ' ∫
xα ⋅xβdA,
A'
A
A
skąd
⎧⎪
Mγ'
= Mα ⋅aαγ'
,
(f)
⎨
⎩⎪ Bγ ' δ ' = Bαβ ⋅aαγ ' ⋅aβδ
'.
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 7
Wzory (f) definiują transformację wektora i tensora przy obrocie układu współrzędnych w przestrzeni
dwuwymiarowej, co wykazuje, że rzeczywiście momenty statyczne są współrzędnymi wektora, a momenty
bezwładności − współrzędnymi tensora. Podobnie jest i w przestrzeni trójwymiarowej, gdzie momenty
bezwładności tworzą dziewięć współrzędnych tensora symetrycznego, zdefiniowanych następująco
(Karaśkiewicz [24]):
⎡ ⎤
(g) Bij = B ji = ⎢ xk xk
⋅dV ⎥
ij xi x j dV i j
⎢∫
⎥ ⋅ δ − ∫
⋅ ; ( , = 123 , , ).
⎣V
⎦ V
Tensor bezwładności figury płaskiej jest reprezentowany przez macierz:
(h) J = ⎡ J
⎣ ⎢ y Jxy⎤
J J
⎥ .
yx x ⎦
Z postaci tej wnioskujemy, że niezmienniki tensora bezwładności są opisane wzorami (por. również wzory
(22.9) i (22.10)):
(i) I1 = I2
= Jb = Jx + Jy = Jx' + Jy' = JI + JII = const > 0,
(j)
Jy
Jxy
2 2
I3
= = Jy⋅Jx − Jxy = Jy' Jx' − Jx' y' = JI⋅ JII = const > 0.
Jyx
Jx
22.5. WSKAZÓWKI PRAKTYCZNE
Analogia między momentami bezwładności a płaskim stanem naprężenia nie jest jednak pełna. Istotna
różnica polega na tym, że osiowe momenty bezwładności są zawsze dodatnie, podczas gdy naprężenia
normalne mogą być również ujemne. Okoliczność ta nakłada pewne warunki na wartość momentów bezwładności.
Ponieważ I3 = JI⋅ JII > 0 , więc zgodnie ze wzorem (j) w p. 22.4 musi zachodzić nierówność:
2
Jx ⋅Jy − Jxy
> 0,
skąd
(a) Jxy < Jx ⋅ Jy
.
2 2 2
Z nierówności ( x− y)
= x + y − 2xy
> 0 wynika dalej, że
Jx + Jy − 2Jxy
> 0,
skąd
Jx
+ Jy
(b)
J xy < .
2
Ze wzoru (a) wynika, że wartość bezwzględna momentu dewiacyjnego musi być mniejsza od średniej
geometrycznej osiowych momentów bezwładności. Ze wzoru (b) wynika natomiast, że moment dewiacyjny
musi być mniejszy od średniej arytmetycznej osiowych momentów bezwładności. Ponieważ średnia
geometryczna nigdy nie jest większa od średniej arytmetycznej, zatem miarodajna jest nierówność
(a), którą można zapisać następująco:
− Jx ⋅ Jy < Jxy < Jx ⋅Jy . (22.13)
Nierówność (22.13) dowodzi, że dowolna trójka liczb nie tworzy tensora bezwładności. Nierówność ta −
słuszna również dla dowolnego, nieśrodkowego układu współrzędnych − jest właściwie jedynym sposobem
kontroli ilościowej obliczonych wartości J x , J y , J xy .
Gdy korzysta się z gotowych wzorów lub tablic należy ustalić właściwy znak momentu dewiacyjnego.
Najczęściej zdarza się to w przekrojach trójkątnych lub kątownikach. O znaku J xy decyduje położenie
ramion kątownika (lub trójkąta). Rozróżniamy tu 4 przypadki przedstawione na rys. 22.7.
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 8
Rys. 22.7
W tablicy IV podano parametry geometryczne najczęściej spotykanych figur płaskich.
Tablica IV
22.6. PRZYKŁAD LICZBOWY
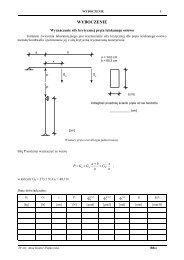
Dany jest przekrój złożony, przedstawiony na rys. 22.8.
Obliczyć:
a) położenie środka ciężkości,
b) momenty bezwładności względem osi środkowych x0, y0,
c) kierunki środkowych osi głównych,
d) główne środkowe momenty bezwładności,
e) momenty bezwładności względem osi środkowych x0'
, y0'
, obróconych względem osi x0, y0
o kąt
ϕ = −40°.
Obliczenia zilustrować kołem Mohra.
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 9
Rys.22.8
Rozwiązanie
Przekrój składa się z czterech elementów. Dla kształtowników walcowanych (elementy 1, 3 i 4) odczytano
z tablic:
Element 1. L120×80×10
2
A= 19, 2 cm , ey
= 1, 96 cm, ex
= 3, 93 cm,
4 4 4
tgϕ0
= 0, 436, Jmin
= 57, 7 cm , Jx
= 279 cm , Jy
= 99, 6 cm .
Element 3. L100×100×8
2
A= 15, 5 cm , ey
= ex
= 2, 74 cm,
4 4 4
Jmin
= 59, 9 cm , Jmax
= 230 cm , Jx
= Jy
= 145 cm .
Element 4.[ 200
A= 32, 2 cm 2 , e= 2, 01cm, Jx
= 1910 cm 4 , Jy
= 148 cm
4 .
Zasadnicze obliczenia odniesiono do pomocniczego układu współrzędnych x, y
(por. rys. 22.8).
a) Obliczenie współrzędnych środka ciężkości całego przekroju
Obliczenie wykonamy według wzorów (22.6):
Ax i i
Ay i i
(a)
xc
= , yc
= .
∑ Ai
∑ Ai
Współrzędne x 1 , y 1 obliczamy ze wzorów na obrót układu:
(b)
∑
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
∑
x1 = x' 1cos ϕ + y' 1sin ϕ,
y1 =− x'sin 1 ϕ + y'cos 1 ϕ,
o
gdzie ϕ =− α =− arctg( 20 / 15) = 5313 , jest kątem obrotu układu x', y' względem układu x, y (kierunek
obrotu układu x', y' przy przejściu do układu x, y jest zgodny
z ruchem wskazówek zegara i stąd znak minus). Obliczenie pozostałych wartości
x i , y i nie wymaga komentarzy.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 10
Element 1
o
o
sinϕ
= sin( − 53, 13 ) = − 0, 80; cosϕ
= cos( − 53, 13 ) = 0, 60,
x' 1= 8 − 1, 96 = 6, 04 cm, y' 1= 3, 93 + 1, 0 = 4, 93 cm,
x1
= 6, 04 ⋅ 0, 60 + 4, 93⋅( − 0, 80) = −0,
32 cm,
y1
=−6, 04 ⋅( − 0, 80) + 4, 93⋅ 0, 60 = 7,
70 cm.
Element 2
x2
= 750 , cm,
y2
= 10, 00 cm.
Element 3
x3
= 15, 00 + 2, 00 + 10, 00 − 2, 74 = 24, 26 cm,
y3
= 20, 00 − 2, 74 = 17, 26 cm.
Element 3
x4
= 15, 00 + 2, 00 + 10, 00 + 2, 01 = 29, 01cm,
y4
= 10, 00 cm.
Tablica V
Sumowania występujące we wzorach (a) wykonano w tablicy V. Współrzędne środka ciężkości całej
2 3 3
figury ( A= 116, 9 cm , Sy
= 1679, 0 cm , Sx
= 1239,
1cm ):
1679,
0
1239,
1
xc
= = 14, 36 cm , yc
= = 10, 60 cm .
116,
9
116,
9
Zwróćmy uwagę na to, że środek ciężkości całego przekroju musi leżeć w obrębie wieloboku utworzonego
przez połączenie środków ciężkości figur składowych.
W naszym zadaniu wymaganie to jest spełnione (por. rys. 22.8).
b) Obliczenie momentów bezwładności względem osi środkowych x0,
y0
Współrzędne środków ciężkości w układzie osi środkowych dla poszczególnych figur składowych
obliczamy ze wzorów:
⎧ xci = xi −xc,
(c)
⎨
⎩ yci = yi − yc.
Momenty bezwładności względem osi środkowych wyznaczamy na podstawie wzorów Steinera:
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

(d)
Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 11
∑
( ) ( )
i
i
∑
2 2
Jx = Jx + Ai ⋅ yci = Jx + Ai yi − yc
,
0 0 0
i
i i
2 2
Jy = ( Jy Ai xci) Jy Ai( xi xc)
0 ∑ + ⋅ =
0i
∑ +
0i
∑ − ,
i
i i
Jx y = Jx y + Ai⋅ xciyci = Jx y + Ai xi−xc ⋅ yi−
y
0 0 0 0 0 0
y
i
i
i
∑
∑( ) ( )
i i ∑ i i ∑ ( ).
Wyznaczenie momentów bezwładności poszczególnych figur względem własnych osi środkowych,
równoległych do osi x0 i y0, tzn. Jx , Jy , J
0i 0i x0iy
, wymaga pewnych dodatkowych obliczeń.
0i
Element 1
Najpierw trzeba ustalić momenty bezwładności dla osi x01 i y01. Na podstawie tablic otrzymujemy:
Jx
= 279 cm 4 , Jy
= 99, 6 cm
4 .
Moment dewiacyjny J x 01 y 01
Jmin = J II , jak i tgϕ 0 .
Sposób 1. Ponieważ JI
+ JII
= Jx
+ Jy
01 01
można wyznaczyć kilkoma sposobami, ponieważ znamy zarówno
01'
01'
4
więc : JI = Jx
+ Jy
− JII = 279, 0 + 99, 6 − 57, 7 = 320, 9 cm .
01'
01'
Ze wzoru (22.10) na obliczenie niezmiennika I 3 otrzymujemy:
skąd
,
2
Jx Jy − J = J J ,
x y I II
01' 01' 01' 01'
Jx ' y ' = Jx ' Jy
' − JI JII = 279 ⋅99, 6 −320, 9 ⋅ 57, 7 = 96,
3 cm > 0,
01 01 01 01
bo w układzie osi x'
01 , y'
01 kątownik jest w położeniu dodatnim.
o
Sposób 2. Ze wzoru na obliczenie tg2ϕ 0 mamy ( 2ϕ 0 = 2arctg( 0, 436) = 47, 11 ):
Jx
J
01' − y01'
279 − 99,
6
4
Jx01 ' y
2
01 ' =
⋅ tg ϕ 0 , J x 01'
y
47 11 96 6
01'
= ⋅ tg , °= , cm .
2
2
Sposób 3. Ze wzoru transformacyjnego na J xy , wyrażonego przez główne momenty bezwładności
JI
i JII, mamy:
J J 320, 9 57,
7
4
Jx01' y
2
47 11 96 4
01' = I − II −
⋅ sin ϕ =
⋅ sin , °= , cm .
2
2
4
Do dalszych obliczeń przyjmujemy, że J x 01' y 96 5
01' = , cm . W celu obliczenia Jx , Jy , J
01 01 x01y01
wykorzystamy wzory transformacyjne na obrót układu z położenia x' 01 , y'
01 do położenia x01, y01
o kąt
α = −53,13°.
279 + 99, 6 279 − 99,
6
4
Jx
= + cos( −25313 ⋅ , ° ) −965 , ⋅sin( −25313
⋅ , ° ) = 256,8 cm ,
01
2 2
4
J y = 279 + 99. 6 − 256, 8 = 121,8 cm ,
01
279 − 99,
6
4
Jx01y
= sin( −25313 ⋅ , ° ) + 965 , ⋅cos( −25313
⋅ , ° ) = −113,1cm
.
01
2
4
Element 2 (blacha 250 mm×20 mm)
Momenty bezwładności względem osi x02'
i y02'
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 12
3
3
25, 0⋅2,
0
4 20 , ⋅250
,
4
Jx
16 7 J
02 ' = = , cm ; y
2604 2
02 ' = = , cm .
12
12
Ponieważ osie x' 02 , y'
02 są głównymi osiami bezwładności, więc J x 02 ' y 0
02 ' = . Momenty bezwładności
względem osi środkowych x02 i y02
obliczymy podobnie jak dla elementu 1:
16, 7 + 2604, 2 16, 7 − 2604,
2
4
Jx
=
+
⋅cos( −25313 ⋅ , ° ) = 16727 , cm ,
02
2
2
4
J y = 16, 7 + 2604, 2 − 1672, 7 = 948, 2 cm ,
02
16, 7 − 2604,
2
4
Jx02 y =
sin( −25313 ⋅ , ° ) = 12420 , cm .
02
2
Element 3
Moment dewiacyjny J x 03 y 03
4
Jx
= J
03 y = 145 cm .
03
obliczymy ze wzorów transformacyjnych wiedząc, że główne osie
bezwładności są pochylone pod kątem −45° w stosunku do osi x , y , a J I = 230 cm
i
4
J II = 60 cm
230, 0 − 66,
0
4
J x 03 y =
sin( −245 ⋅ ° ) = −850
, cm .
03
2
Element 4
Osie x04 i y04
są głównymi osiami bezwładności ceownika. Mamy więc:
4 4
Jx = 1910 cm , Jy = 148 cm , Jx y = 0.
04 04 04 04
03 03
4
Dalsze obliczenia według wzorów (d) zamieszczono w tablicy. Momenty bezwładności całego przekroju
względem osi środkowych x0, y0wynoszą więc:
∑
∑
2 4
Jx
= Jx
+ Ai( yi − yc) = 3984, 5+ 868, 7 = 4853, 2 cm ,
0 0i
i i
2 4
Jy
= Jy
Ai xi x
0 ∑ +
0i
∑ ( − c) = 1363, 0 + 14920, 6 = 16283, 6 cm ,
i i
4
Jx y = Jx y + Ai xi −xc yi − y
0 0 ∑ 0i
0i
∑ ( )( c) = 1043, 9 + 1736, 8 = 2780, 7 cm .
i
i
Sprawdzenie poprawności uzyskanych rezultatów jest w ogólności niemożliwe. Jednak w celu
wychwycenia oczywistych błędów warto zdać się na intuicję oraz sprawdzić nierówności (22.13). W
naszym zadaniu przekrój jest rozbudowany wzdłuż osi x 0 , jest więc intuicyjnie oczywiste, że moment
bezwładności J y0 musi być wyraźnie większy od momentu bezwładności J x0 . Można też oszacować
„na oko” znak momentu dewiacyjnego, rozpatrując rozmieszczenie materiału w poszczególnych
ćwiartkach układu x 0 , y 0 . Na rysunku 22.8 widać, że większa część materiału jest rozmieszczona w
ćwiartkach I i III (ćwiartki dodatnie), a więc moment dewiacyjny J x 0 y powinien być większy od zera.
0
Tak wiec przesłanki intuicyjne potwierdzają poprawność uzyskanych wyników. Również nierówności (a)
i (b) z p. 22.5 są spełnione:
4 4
J xy = 2780, 7 cm < 4853, 2 ⋅ 16283, 6 = 8890,
56 cm ,
4 4853, 2 + 16283,
6
4
J xy = 2780,
7 cm <
= 10568,
4 cm .
2
Powyższa krytyczna ocena uzyskanych rezultatów jest konieczna, gdyż − jak wykazuje doświadczenie
− największe błędy popełniamy właśnie podczas obliczania wyjściowych wartości momentów bezwładności.
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 13
c) Obliczenie kierunków środkowych osi głównych
Położenie środkowych osi głównych I i II jest określone przez kąt ϕ 0 :
2Jx0y0
227807 ⋅ ,
25,
94° tg2ϕ0 =− =−
= 04865 , , skąd ϕ0
= = 12, 97 ° .Ponieważ Jx
< Jy
,
0 0
Jx
− J 4853 2 −16283 6
2
0 y , ,
0
więc kąt ϕ 0 jest kątem między osią x 0 a osią II.
d) Obliczenie głównych środkowych momentów bezwładności
2
4853, 2 + 16283, 6 ⎛ 4853, 2 − 16283,
6⎞
2
4
JI
=
+ ⎜
⎟ + 2780, 7 = 16924,
2cm ,
2 ⎝ 2 ⎠
2
4853, 2 + 16283, 6 ⎛ 4853, 2 − 16283,
6⎞
2 4
JII
=
− ⎜
⎟ + 2780, 7 = 4212, 6 cm .
2 ⎝ 2 ⎠
Sprawdzimy jeszcze wartość niezmiennika I 3 :
7 8
I3
= JI⋅ JII = 16924, 2 ⋅ 4212, 6 = 7, 129 ⋅ 10 cm = Jx ⋅Jy − J
0 0 x0y0 2 .
e) Obliczenie momentów bezwładności względem osi x' 0, y'
0, obróconych względem osi x0, y0
o
kąt ϕ = −40°.
Do obliczenia wykorzystujemy wzory transformacyjne:
4853, 2 + 16283, 6 4853, 2 −16283,
6
4
Jx0'
=
+
cos( − 80° ) −2780, 7sin( − 80° ) = 12314, 4 cm ,
2
2
4
Jy
4853 2 16283 6 12314 4 8822 4
0'
= , + , − , = , cm ,
4853, 2 −16283,
6
4
Jx0'
y
80 2780 7 80 6111 2
0'
=
⋅sin( − ° ) + , ⋅cos( − ° ) = , cm .
2
Sprawdzenie I 3 :
2 7
I 3 12314 4 8822 4 6111 2 7 129 10
= , ⋅ , − , = , ⋅ cm 8 .
Rezultaty obliczeń zawartych w punktach c), d) i e) sprawdzono za pomocą koła Mohra (rys. 22.9). Z
rysunku odczytano (w nawiasach podano wartości ścisłe):
o
ϕ 0 = 13
o
( 12, 97 ),
4
JI
= 16940 cm
4
( 16924, 2 cm ),
JII
=
4
4200 cm
4
( 4212, 6 cm ),
4 4
Jx
= 12390 12314 4
0 ' cm ( , cm ),
4 4
J y = 8780 cm 8822 4 cm
0'
( , ),
4 4
Jx
= 6110 cm ( 6111, 2 cm ).
0'
y0'
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater

Dodatek 22. PARAMETRY GEOMETRYCZNE FIGUR PŁASKICH 14
Rys. 22.9
Andrzej Gawęcki - „Mechanika materiałów i konstrukcji prętowych” 2003r.
Alma Mater