2. Nelinearne enaÄbe

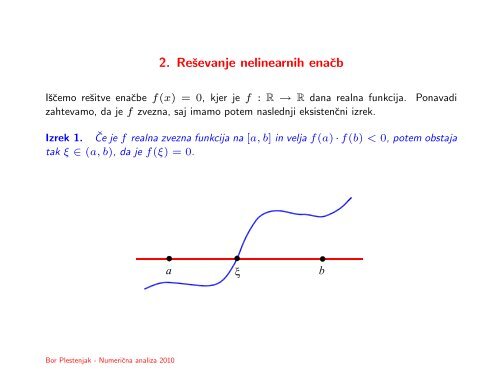
2. Reševanje nelinearnih enačb 

Iščemo rešitve enačbe f(x) = 0, kjer je f : R → R dana realna funkcija. 

zahtevamo, da je f zvezna, saj imamo potem naslednji eksistenčni izrek. 

Ponavadi 

Izrek 1. Če je f realna zvezna funkcija na [a, b] in velja f(a) · f(b) < 0, potem obstaja 

tak ξ ∈ (a, b), da je f(ξ) = 0. 

a 

x 

b 

Bor Plestenjak - Numerična analiza 2010

2.1 Bisekcija 

Ponavadi ne obstaja tako predstavljivo število x ∗ , da bi bilo f(x ∗ ) eksaktno nič. Pri 

bisekciji iščemo čim manjši interval [a, b], na katerem je funkcija f v krajiščih različno 

predznačena. 

function c = bisekcija(f,a,b,ɛ) 

while |b − a| > ɛ|b| 

end 

c = a + (b − a)/2 

if sign(f(a)) = sign(f(c)) 

else 

end 

a = c 

b = c 


Bisekcija 

• Zakaj namesto c = (a+b)/2 uporabljamo c = a+(b−a)/2 fl((a+b)/2) lahko 

ne leži na [a, b]. V P (10, 4, −10, 10) tako npr. za a = 0.6666 in b = 0.6667 

dobimo fl((a + b)/2) = 0.6665. 

◦ Zakaj ne uporabljamo pogoj |b − a| > ɛ Namesto relativnega pogoja lahko vzamemo 

tudi absolutnega, a moramo paziti. V enojni natančnosti npr. iz a = 1000 in b = 1001 

ne moremo dobiti intervala, za katerega bi veljalo |b − a| ≤ 10 −10 . 

• Zakaj ne testiramo, če je fc = 0 

Ker ta pogoj skoraj nikoli ni izpolnjen. 

• Zakaj namesto fa · fc > 0 preverjamo sign(fa) = sign(fc) Računanje produkta 

fa · fc je zahtevnejše od preverjanja predznakov, poleg tega pa se tudi izognemo 

možnim težavam zaradi podkoračitve ali prekoračitve. 

• Metoda očitno odpove pri sodih ničlah. 

• Bisekcijo lahko uporabljamo tudi za iskanje lihih polov, računati pa moramo na težave 

zaradi prekoračitve v bližini pola. 

• Če je na [a, b] več rešitev, bisekcija najde le eno. 

• V vsakem koraku se napaka približno razpolovi. 


Zgled: Z bisekcijo poiščimo ničle funkcije f(x) = x − tan(x). 

Težko je poiskati dober začetni interval, saj so ničle v bližini polov. Rešitev je, da namesto 

f iščemo ničle g(x) = x cos(x) − sin(x). Sedaj nimamo težav s poli. 


2.2 Navadna iteracija 

Pri navadni iteraciji enačbo f(x) = 0 zapišemo v obliki x = g(x) in nato delamo iteracijo 

x r+1 = g(x r ), r = 0, 1, . . .. Funkcijo g imenujemo iteracijska funkcija. 

Zgledi iteracijskih funkcij: 

• g(x) = x − f(x), 

• g(x) = x − Cf(x), kjer je C ≠ 0, 

• g(x) = x − h(x)f(x), kjer je h(x) ≠ 0. 


Zgled : Iz grafa polinoma p(x) = x 3 − 5x + 1 

vidimo, da ena ničla leži blizu 0. Enačbo zapišemo v obliki x = 1+x3 

5 

in tvorimo zaporedje 

približkov 

x 0 = 0 

x r+1 = 1+x3 r 

5 

, r = 0, 1, . . . 

To zaporedje skonvergira k α = 0.210639676 . . .. Iterativna funkcija je dobra le za 

srednjo ničlo. Do ostalih dveh korenov pridemo npr. z iteracijo x r+1 = 3√ 5x r − 1. 


Konvergenca navadne iteracije 

Naj bo α koren enačbe x = g(x). O konvergenci v bližini korena odloča g ′ (α). Če je 

|g ′ (α)| < 1, imamo privlačno točko, sicer pa odbojno točko. 

Izrek 2. Naj bo α koren enačbe x = g(x), naj bo g zvezno odvedljiva in naj velja 

|g ′ (α)| < 1. Potem obstaja taka okolica I za α, da za vsak x 0 ∈ I zaporedje 

konvergira k α. 

x r+1 = g(x r ), r = 0, 1, . . . 

Dokaz. Naj bo e k = x k − α napaka približka x k . 

Velja 

e k+1 = x k+1 − α = g(x k ) − g(α) = g ′ (ξ k )(x k − α), 

kjer je ξ k točka med x k in α. 

Če začnemo dovolj blizu α, potem zaradi |g ′ (α)| < 1 obstaja konstanta C < 1, da je |g ′ (ξ k )| ≤ C < 1. 

Tako dobimo 

|e k+1 | ≤ C|e k | ≤ C 2 |e k−1 | ≤ · · · ≤ C k |e 0 | 

in ko gre k → ∞ gre x k → α. 


Red konvergence 

Definicija 3. 

velja 

Red konvergence je p, če v bližini α obstajata konstanti C 1 , C 2 > 0, da 

C 1 |x r − α| p ≤ |x r+1 − α| ≤ C 2 |x r − α| p . 

Lema 4. Naj bo iteracijska funkcija g v okolici negibne točke α p-krat zvezno odvedljiva 

in naj velja g (k) (α) = 0, k = 1, . . . , p − 1 in g (p) (α) ≠ 0. Potem ima iteracija 

x r+1 = g(x r ), r = 0, 1, . . ., v bližini rešitve red konvergence p. 

Dokaz. 

Iz razvoja g v Taylorjevo vrsto okrog α dobimo g(x) = α + 1 p! (x − α)p g (p) (ξ). 

Posebni primeri konvergence: 

• p = 1: linearna (konstantno korakov za novo točno decimalko) 

• p = 2: kvadratična (število točnih decimalk se v vsakem koraku podvoji) 

• p = 3: kubična (število točnih decimalk se v vsakem koraku potroji) 

• 1 


Primerjava nekaterih iteracijskih funkcij za enačbo x 2 + ln x = 0. 

Za enačbo x 2 + ln x = 0, ki ima rešitev α = 0.6529186, primerjamo tri iteracijske 

funkcije: 

• g 1 (x) = e −x2 , g ′ 1 

(α) = −0.853, red je 1, 

• g 2 (x) = 1 2 (x + e−x2 ), g ′ 2 

(α) = 0.074, red je 1, 

• g 3 (x) = 2x3 +e −x2 

1+2x 2 , g ′ 3 

(α) = 0, red je 2. 

Za različne začetne približke smo primerjali število iteracij dokler se zaporedna približka ne 

razlikujeta za manj kot 10 −12 . 

x 0 0.6 0.7 1 10 100 

g 1 163 162 173 175 175 

g 2 14 14 15 18 21 

g 3 5 5 7 109 10013 


2.3 Newtonova ali tangentna metoda 

Naj bo x približek za ničlo funkcije f. 

v Taylorjevo vrsto 

Če upoštevamo le prva dva člena v razvoju f(x + h) 

f(x + h) = f(x) + f ′ (x)h + f ′′ (x)h 2 

2 

+ · · · , 

dobimo 

f(x + h) ≈ f(x) + f ′ (x)h. 

Če predpostavimo, da je f ′ (x) ≠ 0, iz enačbe f(x+h) = 0 dobimo h ≈ −f(x)/f ′ (x). 

Ker je to le približek, postopek ponavljamo: 

r = 0, 1, . . . 

x r+1 = x r − f(x r) 

f ′ (x r ) 

Izpeljali smo tangentno oz. Newtonovo metodo. 


Geometrijska izpeljava 

Pri tangentni metodi funkcijo f aproksimiramo s tangento v točki (x r , f(x r )) in za 

naslednji približek vzamemo presečišče tangente z osjo x. 

x r+1 = x r − f(x r) 

f ′ (x r ) 

Analitično je tangentna metoda posebna oblika navadne iteracije, kjer za iteracijsko funkcijo 

vzamemo 

g(x) = x − f(x) 

f ′ (x) . 


Red konvergence tangentne metode 

g(x) = x − f(x) 

f ′ (x) , 

z odvajanjem dobimo g′ (x) = f(x)f ′′ (x) 

. 

f ′2 (x) 

Če je α enostaven koren, dobimo g ′ (α) = 0 in konvergenca tangentne metode je vsaj 

kvadratična. V tem primeru je 

g ′′ (α) = f ′′ (α) 

f ′ (α) , 

torej je v primeru f ′′ (α) ≠ 0 konvergenca kvadratična, sicer pa vsaj kubična. 

Če je α večkratni koren, je konvergenca linearna, izkaže se, da za m-kratno ničlo velja 

lim x→α g ′ (x) = 1 − 1 m . 

Konvergenca tangentne metode je 

• kvadratična: enostaven koren in f ′′ (α) ≠ 0 (standardna situacija), 

• linearna: večkratni koren, 

• vsaj kubična: enostaven koren in f ′′ (α) = 0. 


Zgled za tangentno metodo 

Poglejmo polinom p(x) = x 4 − 11 2 x3 + 21 2 x2 − 8x + 2 = (x − 1 2 )(x − 1)(x − 2)2 . 

Če vzamemo začetne približke 0.6, 1.1 in 2.1 opazimo, da imamo pri 0.6 kvadratično 

konvergenco, pri 1.1 kubično konvergenco (prevoj) in pri 2.1 linearno konvergenco (dvojna 

ničla). 


1: 0.435294117647059 

2: 0.489337730251386 

3: 0.499639486749880 

4: 0.499999567515696 

5: 0.499999999999377 

6: 0.500000000000000 

7: 0.500000000000000 

Zgled za tangentno metodo 

1: 0.994117647058826 

2: 1.000001228818246 

3: 1.000000000000001 

4: 1.000000000000001 

1: 2.053562005277051 

2: 2.027876685351187 

3: 2.014247493817868 

4: 2.007206326821148 

5: 2.003624539543750 

6: 2.001817710121426 

7: 2.000910227515493 

8: 2.000455458435571 

9: 2.000227815584859 

10: 2.000113929407939 

11: 2.000056970115901 

12: 2.000028486376981 

13: 2.000014243467003 

14: 2.000007121897697 

15: 2.000003561048605 

16: 2.000001780574947 

17: 2.000000890692019 

18: 2.000000447946005 

19: 2.000000223231179 

20: 2.000000111826573 

21: 2.000000069466783 

22: 2.000000018324164 

23: 2.000000018324164 


Konvergenčni izreki za tangentno metodo 

Pri enostavni ničli imamo vedno konvergenco, če je začetni približek dovolj dober. 

Izrek 5. Naj bo α enostavna ničla dvakrat zvezno odvedljive funkcije f. Potem obstajata 

okolica I točke α in konstanta C, da tangentna metoda konvergira za vsak x 0 ∈ I in da 

približki x r zadoščajo oceni 

|x r+1 − α| ≤ C(x r − α) 2 . 

Pri določenih pogojih lahko dokažemo tudi globalno konvergenco iz poljubne začetne točke. 

Izrek 6. Naj bo f na intervalu I = [a, ∞) dvakrat zvezno odvedljiva, naraščajoča in 

konveksna funkcija, ki ima ničlo α ∈ I. Potem je α edina ničla f na I in za vsak x 0 ∈ I 

tangentna metoda konvergira k α. 


Tangentna metoda potrebuje dobre začetne priblžke 

Izreki nam zagotavljajo konvergenco tangentne metode dovolj blizu ničle ali pa za funkcijo 

prave oblike. Sicer pa imamo lahko zelo različno obnašanje in slepa uporaba tangentne 

metode ni priporočljiva. Naslednja dva primera kažeta divergenco, ko nismo dovolj blizu 

ničle in zaciklanje približkov. 


Tangentna metoda v kompleksnem 

Tangentno metodo lahko uporabljamo tudi za računanje kompleksnih korenov enačb. Naj 

bo f analitična funkcija in naj velja f ′ (z 0 ) ≠ 0. Označimo ploskev w(z) = |f(z)| nad 

kompleksno ravnino. Kompleksno število 

z 1 = z 0 − f(z 0) 

f ′ (z 0 ) , 

ki ga dobimo po enem koraku tangentne metode, je presečišče dveh premic: 

• presečišča tangentne ravnine na ploskev w = |w(z)| v točki (z 0 , w(z 0 )) z ravnino 

w = 0, 

• projekcije gradienta na ploskev w = |w(z)| v točki (z 0 , w(z 0 )) na ravnino w = 0. 

Če imamo npr. polinom z realnimi koeficienti in iščemo kompleksno ničlo, potem moramo 

uporabiti kompleksni začetni približek, sicer bodo vsi približki realni. 


2.4 Sekantna metoda 

Namesto tangente uporabljamo sekanto, potrebujemo dva začetna približka: 

x r+1 = x r − 

x r − x r−1 

f(x r ) − f(x r−1 ) f(x r), r = 1, 2, . . . . 

Analitično f ′ (x r ) aproksimiramo z diferenčnim kvocientom f(x r) − f(x r−1 ) 

x r − x r−1 

. 


Lastnosti sekantne metode 

◦ Ne spada med navadno iteracijo, saj je naslednji približek odvisen od dveh zadnjih. 

◦ Ne potrebujemo odvodov. 

◦ V vsakem koraku izračunamo le eno vrednost funkcije (razen v prvem). 

◦ Red konvergence je 1.62 oz. (1 + √ 5)/2, kar pomeni, da je superlinearna. 

Pri tangentni metodi število točnih decimalk narašča kot 

pri sekantni metodi pa kot 

1, 2, 4, 8, 16, 

1, 1.6, 2.6, 4.1, 6.6, 10.5, 16.8. 

Za maksimalno natančnost v dvojni natančnosti tako pri tangentni metodi potrebujemo 4 

korake in izračun 4f in 4f ′ . Pri sekantni metodi porabimo 6 korakov in izračun 7f. To 

pomeni, da je glede na porabljeno delo sekantna metoda lahko celo boljša od tangentne. 


2.5 Inverzna interpolacija 

Posplošitev sekantne metode je, da vzamemo zadnje tri približke x r , x r−1 , x r−2 in funkcijo 

f aproksimiramo s parabolo skozi točke (x r , f(x r )), (x r−1 , f(x r−1 )), (x r−2 , f(x r−2 )). 

Tako dobimo Mullerjevo metodo. Uporabna je za iskanje kompleksnih ničel z realno 

aritmetiko, saj ima dobljena parabola lahko kompleksni ničli. Red konvergence je 1.83, so 

pa težave, kadar ni jasno, katero izmed dveh ničel izbrati. 

Obratni pristop je, da zamenjamo vlogi x in y ter poiščemo kvadratni polinom p, za katerega 

velja p(f(x r )) = x r , p(f(x r−1 )) = x r−1 , p(f(x r−2 )) = x r−2 . Naslednji približek je 

potem kar x r+1 = p(0). To je inverzna kvadratna interpolacija, red konvergence pa je 

1.83 kot pri Mullerjevi metodi. 

Mullerjeva m. 

inv. kvad. int. 


2.6 Kombinirana metoda 

S kombiniranjem različnih metod lahko dosežemo robustnost in hitro konvergenco. Če 

imamo tak začetni interval [a, b], da je f(a)f(b) < 0, potem lahko npr. kombiniramo 

bisekcijo, sekantno metodo in inverzno kvadratno interpolacijo: 

a in b preuredimo tako, da je |f(b)| ≤ |f(a)| ter vzamemo c = a. 

Dokler ni |a − b| < ɛ ponavljaj 

a) Izračunaj s: če je c ≠ a naredi en korak inverzne kvadratne interpolacije, sicer pa 

sekantne metode. 

b) Če je izpolnjen kateri izmed naslednjih pogojev, naredi korak bisekcije in vzemi s = 

(a + b)/2: 

• s ne leži med (3a + b)/4 in b, 

• v prejšnjem koraku je bila uporabljena bisekcija in |s−b| ≥ |b−c|/2 ali |b−c| < δ, 

• v prejšnjem koraku ni bila uporabljena bisekcija in |s−b| ≥ |c−d|/2 ali |c−d| < δ. 

c) d = c, c = b, glede na predznak f(s) zamenjaj a oziroma b z s. 

d) Po potrebi medsebojno zamenjaj a in b, da je |f(b)| ≤ |f(a)|. 

Ker nam točka nikoli ne pade iz [a, b], imamo zagotovljeno konvergenco, ki je v bližini 

ničle superlinearna. 


2.7 Ničle polinomov 

Pri polinomih pogosto potrebujemo vse ničle polinoma p(x) stopnje n. Tudi če so 

koeficienti polinoma realni, so ničle lahko kompleksne. Za računanje je na voljo več 

pristopov: 

• Z eno izmed navedenih metod (npr. Newtonovo ali Mullerjevo) poiščemo eno ničlo x 1 , 

potem pa obravnavamo polinom q(x) = p(x)/(x − x 1 ) ki je za eno nižje stopnje. To 

ponavljamo, dokler ne izračunamo vseh ničel. Za stabilnost je potrebno ničle izločati 

v pravilnem vrstnem redu, priporočljivo pa je tudi, da na koncu vse ničle vzamemo kot 

začetne približke za originalni polinom p(x) in naredimo še nekaj korakov. 

• Iz polinoma sestavimo t.i. pridruženo matriko A velikosti n × n, katere karakteristični 

polinoma je enak p(x). Ničle polinoma p(x) so potem kar lastne vrednosti matrike A. 

Tako ničle izračuna npr. Matlab z ukazom roots. 

• Uporabimo posebne metode, ki so namenjene samo za polinome, kot so npr. Laguerrova, 

Bairstowova, Jenkins-Traubova metoda, itd. 


Wilkinsonov zgled 

Ničle polinomov so lahko zelo občutljive na motnje koeficientov. Tako ima npr. polinom 

p(x) = (x − 1)(x − 2) · · · (x − 20) = x 20 − 210x 19 + · · · + 20! 

ničle 1, 2, . . . , 20, točne ničle polinoma 

pa so 

g(x) = p(x) − 2 −23 x 19 

x 9 = 8.91752 

x 10,11 = 

. 

10.0953 ± 0.64310i 

x 16,17 = 16.7307 ± 2.81263i 

x 18,19 = 19.5024 ± 1.94033i 

x 20 = 20.8469 

Čeprav so vse ničle enostavne in lepo separirane, majhna motnja povzroči velike spremembe. 


Wilkinsonov zgled, 2. del 

Wilkinson je s pomočjo zgornjega primera pokazal, da je računanje lastnih vrednosti matrike 

preko ničel karakterističnega polinoma lahko nestabilno. Standardni postopek je namreč bil: 

• Vzamemo matriko A ∈ R n×n in izračunamo koeficiente karakterističnega polinoma 

p(x) = a 0 + a 1 x + · · · + a n x n . 

• Z nekim algoritmom za računanje ničel polinoma izračunamo ničle polinoma p(x) in to 

so lastne vrednosti. 

Danes se je postopek obrnil. 

p(x), se zgodi naslednje: 

Če v Matlabu poženete ukaz za računanje ničel polinoma 

• Iz polinoma p(x) se sestavi matrika, katere karakteristični polinoma je p(x). 

• Z algoritmom za računanje lastnih vrednosti se izračunajo lastne vrednosti A in to so 

ničle našega polinoma. 


Reševanje nelinearnih enačb v Matlabu 

V standardni verziji je za iskanje ničle realne funkcije ene spremenljivke na voljo funkcija fzero, ki uporablja 

kombinirano metodo. Oblika je fzero(fun,x0,options,p1,p2,...). 

• S prvim argumentom fun podamo funkcijo, katere ničlo iščemo. Možnosti so: 

◦ v obliki niza z definicijo funkcije, npr. fzero(’cos(x)-x’,0), 

◦ v obliki t.i. inline funkcije, npr. f=inline(’cos(x)-x’); fzero(f,[-1,1]), 

◦ v obliki niza z imenom funkcije, npr. fzero(’cos(x)-x’,0), 

◦ s kazalcem na funkcijo, npr. fzero(@humps,1). 

• Drugi argument x0 je začetni približek, ki je vektor z eno ali dvema komponentama. 

◦ fzero(’cos(x)-x’,[-1,1]): podamo točki, kjer je funkcija različno predznačena, 

◦ fzero(’cos(x)-x’,0): Matlab z iskanjem levo in desno sam išče začetni interval. 

• S tretjim argumentom lahko nastavimo parametre s pomočjo funkcije optimset, npr 

fzero(’cos(x)-x’,0,optimset(’Display’,’iter’,’TolX’,1e-4)). Parametri, ki jih lahko nastavimo 

so: 

◦ ’Display’: ali se izpisujejo tekoči približki, možnosti so ’iter’, ’off’, ’final’. 

◦ ’TolX’: pogoj za konec (ko bo razlika zadnjih dveh približkov pod mejo). 

◦ ’MaxIter’: maksimalno število iteracij. 

◦ ’TolFun’: pogoj za konec (ko bo vrednost funkcije pod mejo). 

• Z naslednjimi argumenti lahko nastavljamo dodatne argumente funkcije fun, če je to funkcija več 

spremenljivk. Zgled je f=inline(’besselj(0,x)-y’,’x’,’y’); fzero(f,[1 2],[],0.5). 


Zgled - dvig tračnice 

h 

d 

d+e 

Imamo 2d dolgo tračnico, ki je na obeh koncih 

trdno vpeta. Tračnica se raztegne za 2e in 

se dvigne v obliki krožnega loka. Izračunaj, 

kolikšna je maksimalna oddaljenost od tal. 

sin φ = d/r in rφ = d + e, torej 

r 

sin φ 

φ = d 

d + e . 

f 

h = (1 − cos φ)r = 2 sin 2 ( φ 

2 

)d + e 

φ . 

Če vzamemo d = 75 in e = 0.005, potem dobimo φ = 0.01999953335176 in nato 

h = 0.75000749994107. 


Večkratne ničle 

Za večkratne ničle velja pravilo, da za m kratno ničlo lahko pravilno izračunamo le 1/m 

decimalk, ki so na voljo. Tako npr. pri dvojni ničli dobimo le polovico, pri trojni ničli pa le 

tretjino točnih decimalk. 

Če vzamemo npr. f(x) = x 4 − 7x 3 + 18x 2 − 20x + 8 = (x − 1)(x − 2) 3 , dobimo s 

tangentno metodo in začetnim približkom 2.1: 

1: 2.067647058823931 

2: 2.045564430808835 

3: 2.030593755171017 

4: 2.020495758352892 

5: 2.013709272420485 

6: 2.009160022769000 

7: 2.006115892225148 

8: 2.004081383953162 

. . . . . 

33: 1.999951585932835 

34: 1.999968259875404 

35: 1.999975900893329 

36: 1.999986096735057 

37: 1.999986096735057 


Dogajanje v okolici večkratne ničle 

Poglejmo si računanje vrednosti polinoma 

x 9 − 18x 8 + 144x 7 − 672x 6 + 2016x 5 − 4032x 4 + 5376x 3 − 4608x 2 + 2304x − 512, 

ki je razčlenjen izraz (x − 2) 9 , v okolici točke 2. Z Matlabom dobimo 


Dogajanje v okolici večkratne ničle, 2.del 

Napake niso povsem naključne, temveč tvorijo vzorec, ki ga opazimo, če pogledamo izračun 

pri prvih 2000 predstavljivih številih večjih od 2: 


Sledenje implicitno podane funkcije 

Denimo, da bi radi narisali graf krivulje, ki je implicitno podana z enačbo f(x, y) = 0. 

Potrebujemo torej čim več točk (x i , y i ), za katere velja f(x i , y i ) = 0. 

Če je (x 0 , y 0 ) točka na krivulji, potem lahko pričakujemo, da se bo ob majhni spremembi 

x malo spremenil tudi y. Tu lahko uporabimo tangentno metodo, saj ima kvadratično 

konvergenco in vedno konvergira, če je začetni približek dovolj dober. Tako lahko kot 

začetni približek za f(x 0 + dx, y) = 0 vzamemo kar y 0 . 

Težave se pojavijo, kadar se funkcija obrača, ima večkratne točke in podobno. V teh 

primerih si lahko pomagamo z zamenjavo spremenljivk x in y. Kot kriterij za to, v katero 

smer naj se premikamo, lahko služita parcialna odvoda f po x in y. 

(x 0 

,y 0 

) (x 1 ,y 1 ) (x 2 

,y 2 

) 

(x 3 

,y 3 

) 

(x 4 

,y 4 

) 

Bor Plestenjak - Numerična analiza 2010 

f(x,y)=0

Zgled - sekularna enačba 

Pri računanju lastnih vrednosti simetrične matrike z metodo deli in vladaj je potrebno 

poiskati rešitve sekularne enačbe f(λ) = 0, kjer je 

f(λ) = 1 + 

n∑ 

i=1 

u 2 i 

d i − λ . 

Velja d n < · · · < d 2 < d 1 in 

u i ≠ 0 za i = 1, . . . , n. 

Kako zgleda graf f(λ) Poli so v d i , asimptota je y = 1. Ker je f ′ (λ) = ∑ n 

i=1 

u 2 i 

(d i −λ) 2, 

je f med poli strogo naraščajoča. Ničle ležijo med poli, ena pa desno od zadnjega pola. 

Slika je za primer u = [0.03 0.05 0.05 0.03] in d = [1 2 3 4]. 


Sekularna enačba, 2.del 

Navadne tangentne metode ne moremo uporabiti, saj so ničle lahko zelo blizu polov in 

bi potrebovali zelo dobre približke. Namesto aproksimacije funkcije s tangento zato raje 

uporabimo preprosto racionalno funkcijo, ki se prilega funkciji f. 

Denimo, da iščemo rešitev na intervalu (d i+1 , d i ), začetni približek pa je x r . 

poiščemo racionalno funkcijo oblike 

Sedaj 

h(λ) = c 1 

d i − λ + c 2 

d i+1 − λ + c 3, 

za katero velja h(x r ) = f(x r ) in f ′ (x r ) = h ′ (x r ). 

Enačba h(λ) = 0 ima dve rešitvi, za x r+1 pa vzamemo tisto, ki leži znotraj (d i+1 , d i ). 

Konvergenca je zelo hitra, saj h zelo dobro aproksimira f na intervalu (d i+1 , d i ). 


Sekularna enačba, podrobnosti 

Zaradi stabilnosti razdelimo f na dva dela kot 

f(λ) = 1 + 

i∑ 

k=1 

u 2 k 

d k − λ + 

n∑ 

k=i+1 

u 2 k 

d k − λ =: 1 + ψ 1(λ) + ψ 2 (λ). 

To naredimo zato, da v vsoti za ψ 1 (λ) oziroma ψ 2 (λ) seštevamo enako predznačene člene. 

Sedaj določimo c 1 , c ′ 1 tako, da za h 1 (λ) = c 1 

d i − λ + c′ 1 

velja h 1 (x r ) = ψ 1 (x r ) in h ′ 1 (x r) = ψ ′ 1 (x r). Podobno določimo c 2 , c ′ 2 

tako, da za 

h 2 (λ) = 

c 2 

d i+1 − λ + c′ 2 

velja h 2 (x r ) = ψ 2 (x r ) in h ′ 2 (x r) = ψ ′ 2 (x r). 

iskana racionalna funkcija. 

Sedaj je h(λ) = 1 + h 1 (λ) + h 2 (λ)

2. Nelinearne enaÄbe

Create successful ePaper yourself

Delete template?

Save as template?

2. Nelinearne enaÄbe