Rozwiązywanie belek wieloprzeslowych statycznie ... - Poznań

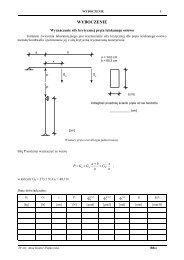
W YKŁ ADY Z MECHANIKI BUDOWLI
ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH
1
Olga Kopacz, Adam Łodygowski, Wojciech Pawłowski,
Michał Płotkowiak, Krzysztof Tymper
Konsultacje naukowe: prof. dr hab. JERZY RAKOWSKI
Poznań 2002/2003
MECHANIKA BUDOWLI 10
ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH
STSTYCZNIE NIEWYZNACZALNYCH.
1.1. Metoda trzech momentów.
Do rozwiązywania wieloprzęsłowych belek statycznie
niewyznaczalnych stosowana jest szczególna postać metody sił, zwana
metodą trzech momentów.
Rozważmy dowolnie obciążoną wieloprzęsłową belkę statycznie
niewyznaczalną (rys.1.1a). Schemat zastępczy ( podstawowy ) statycznie
wyznaczalny może być w tej metodzie przyjęty dowolnie, wprowadzając
przeguby w miejscu podpór
Rys.1.1
Politechnika Poznańska®
Kopacz, Łodygowski, Pawłowski, Płotkowiak, Tymper

W YKŁ ADY Z MECHANIKI BUDOWLI
ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH
2
i przyjmując niewiadome w postaci momentów podporowych (rys.1.1b)
Wówczas otrzymamy macierz podatności w postaci pasmowej!!!
Rozważmy następnie dwa sąsiednie, dowolnie wybrane przęsła
belki (r)
oraz (r-1). Dla przegubu r warunek geometryczny należy zapisać jako
wzajemny kąt obrotu równy zeru:
l p ( r−1,
r)
( r,
r+ 1)
∆
r
= ∆r
+ ∆r
= ∆
r
+ ∆
r
= 0
(1.1)
gdzie:
∆ l r
− to kąt obrotu przekroju belki jednoprzęsłowej r obciążonej na
podporach momentami X
r−1,
X
r
oraz obciążeniem zewnętrznym,
∆ p r
− to kąt obrotu przekroju belki jednoprzęsłowej r + 1obciążonej na
podporach momentami X
r
, X r + 1oraz obciążeniem zewnętrznym.
Wprowadźmy równanie kanoniczne dla r − tego punktu:
δ X δ X + δ X + ... + ∆ 0
(1.2)
r−1 , r r−1
+
rr r r+
1, r r+
1
rp
=
gdzie (patrz rys.1.1b):
M
r−1
⋅ M
r 1 1 1 lr
δ
r−1,
r
= ∫ ds = ⋅ ⋅lr
⋅1⋅
⋅1
=
EI EI 2 3 6EI
δ
δ
r
M
r
⋅ M
r 1 1 2 1 1 2
∫ ds = ⋅ ⋅lr
⋅1⋅
⋅1+
⋅ ⋅l
1
⋅1⋅
⋅1
=
EI EI 2 3 EI 2 3
r, r
=
r+
r
r+
1
1 ⎛ lr
lr+
1
⎞
=
⎜ +
⎟
3 ⎝ EI
r
EI
r+
1 ⎠
M
r+
1
⋅ M
r 1
= ∫ ds =
EI EI
r+ 1, r
⋅ ⋅lr+
1
⋅1⋅
⋅1
=
r+
1
2 3
1
1
r
l
6EI
M
r−1
⋅ M
r+
1
δ r −1,
r+
1
= ∫ ds = 0
EI
Podstawiając do równania (1.2) wyznaczone wartości (1.3)
otrzymujemy:
l 1 ⎛ ⎞
r
lr
lr+
1
lr+
1
X
1
+ +
1
+ ... + ∆ = 0
3
⎜ +
⎟
r−
X
r
X
r+
rp
EI
r ⎝ EI
r
EI
r+
1 ⎠ EI
r+
1
r+
1
r+
1
(1.3)
(1.3)
Politechnika Poznańska®
Kopacz, Łodygowski, Pawłowski, Płotkowiak, Tymper

W YKŁ ADY Z MECHANIKI BUDOWLI
ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH
3
a po uporządkowaniu równanie, zwane równaniem trzech momentów,
przyjmuje postać:
l ′ 2 ( ′ ′ ) ′
r
X
r−1 + ⋅ X
r
lr
+ lr+
1
+ X
r+
1
⋅lr+
1
+ ... + 6EI
0∆
rp
= 0
(1.4)
przy czym:
EI
0
l′ r
= lr
⋅ a , EI
0
-sztywność porównawcza
EI
r
A co z warunkami brzegowymi
Załóżmy, że nasza belka jest belką podpartą z lewej strony
(rys.1.2a).
Moment w punkcie "0" równy jest
zeru! mamy zatem już warunek
brzegowy!(x 0 =0!). Gdyby zaś nasza
belka była z jednej strony
utwierdzona (rys.1.2b) należałoby ją
rozszerzyć o jedno przęsło, i w celu
wyznaczenia warunków brzegowych
założyć że: l = 0
0 . Jeżeli zaś znamy
obciążenie jakie występuje po
zewnętrznej stronie przęsła jak na
rysunku (rys.1.2c), możemy
wyznaczyć wykres momentów co
umożliwia nam wyznaczenie X
0
i
rozpisanie równania dla dwóch
sąsiednich
przęseł z czego otrzymamy szukane warunki brzegowe.
1.2. Linie wpływu dla belek wieloprzęsłowych.
Wyznaczając w układach statycznie niewyznaczalnych linie
wpływu wielkości statycznych, klasyczną metodą sił, wyznacza się
najpierw linie wpływu nadliczbowych, co w dalszej kolejności umożliwi
nam wyznaczenie linii wszystkich innych wielkości.
Wróćmy do naszego przykładu. Przypuśćmy, że po naszej belce
porusza się poziomo siła P (rys.1.3). Ponieważ belka jest statycznie
niewyznaczalna, na nic zdadzą się próby rozwiązania jej, przy pomocy
równań równowagi. W takim przypadku należałoby rozwiązać układ
Politechnika Poznańska®
Kopacz, Łodygowski, Pawłowski, Płotkowiak, Tymper

W YKŁ ADY Z MECHANIKI BUDOWLI
ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH
4
równań liniowych (1.4 ), co pozwoli nam na wyznaczenie wielkości
A ⋅ X = P to w celu wyznaczenia linii wpływu
Jeżeli mamy: [ ] [ ] [ ]
Politechnika Poznańska®
l r
Kopacz, Łodygowski, Pawłowski, Płotkowiak, Tymper
X
r
.
wystarczy macierz [ P]
pomnożyć przez macierz
podatności odwróconą:
[ X ] = [ P] ⋅[ A] −1
Zastanówmy się teraz jak określić ∆
rp
gdy
mamy do czynienia z ruchomym obciążeniem.
Rys.1.3 Spójrzmy na rysunek obok (rys.1.3). Z naszej
belki wycięliśmy jedno przęsło (r-1,r) po
którym jeździ siła P (teraz już w układzie
lokalnym!) Oczywiście efektem jej działania jest wystąpienie sił
wewnętrznych (momentów, tnących...) Spójrz na rysunek 1.1. Stosując
tw. Maxwella wiemy, że
∆ = ∆ , czyli jest to ugięcie belki wywołane
rp
pr
działaniem jednostkowego momentu przyłożonego do podpory „ r ”.
Ugięcie to jest niezerowe tylko dla dwóch przęseł (r-1,r) i (r,r+1) p
wspólnym węźle „ r ”.
Wyznaczamy linię ugięcia od zadanego
momentu. Mamy zatem:
2
d δ ( x)
EI ⋅ = −M
( x)
(1.6)
2
dx
δ
u nas:
M ( x)
= 1 ⋅ x
Rys.1.4
lr
po podstawieniu i dwukrotnym scałkowaniu otrzymujemy:
d
2 2
δ ( x)
1 cakujemy dδ
( x)
x
cakujemy
EI ⋅ = − ⋅ x ⎯⎯⎯
→ EI ⋅ = − + C ⎯⎯⎯
→
2
dx l
dx 2 ⋅ l
3
x
EI ⋅δ
( x)
= −
6 ⋅l
r
r
+ C ⋅ x + D
z warunków brzegowych: δ ( x = 0) = 0 i δ ( x = l r
) = 0 możemy
wyznaczyć szukane D, C . Linia ugięcia od założonego przez nas
momentu jedynkowego równa jest szukanej wartości i wynosi:
3
( ξ − )
r
∆
r, P
2
l
x
δ ( x ) = − ξ gdzie: ξ =
(1.7)
6EI r

W YKŁ ADY Z MECHANIKI BUDOWLI
ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH
5
Wiemy też, że: ∆ r − 1,
P
≠ 0 i ∆
r −1,
P
= ∆
P,
r−1
( ∆ P,r−1
− to
przemieszczenie pionowe pod siłą P wywołane działaniem momentu
skupionego X
r−1
). Jeżeli więc, do równania wyżej (1.7) zgodnie z
rysunkiem (rys.1.5) za ξ podstawimy 1 −ξ
to otrzymamy gotowe
rozwiązanie:
1−ζ
ζ
3 2
( ξ − 3ξ
+ ξ )
2
l
δ ( x ) =
2 (1.8)
6EI r
Wprowadźmy pewną funkcje
3
ω ( ξ ) = ξ − ξ ⇒ . ω(
ξ ) = ξ − 3ξ
2 + 2ξ
,po
podstawieniu mamy:
2
lr
′
6EI 0
= ⋅ω(
ξ ) ⇒ l r
⋅l
r
⋅ω(ξ )
6EI
Rys.1.5
W układzie równań kanonicznych, w przypadku, gdy
wędrująca siła porusza się w obrębie przęsła (r-1,r)
tylko dwa równania mają niezerowe prawe strony, a
mianowicie:
l ′
m
X
m
X
m( l′
m
l′
m
) + X
m
⋅ l′
−1 + 2 ⋅ +
+ 1 + 1 m+
1
= Cmp
(1.9)
dla m = r −1
C ′
r−1,
p
= −lr
⋅lr
⋅ω(
ξ ) oraz
dla m = r
C −l
⋅l′
⋅ω(
)
r, p
=
r r
ξ
Rozwiązując otrzymany układ równań względem niewiadomych
X
1, X
2,...,
X n
otrzymamy:
X
k
() ξ = β
k1 ⋅C1P
+ β
k 2
⋅C2P
+ ... + β
kk
⋅CkP
+ ... + β
k , r−1
⋅Cr−
1,
P
+ (1.10
β
kr
⋅ CrP
+ β
k , r+ 1
⋅Cr+
1, P
+ ... + ...
)
przy czym, współczynniki β
kj
są wyrazami macierzy odwrotnej dla
układu równań (1,9), tzn. są to elementy macierzy odwrotnej, w stosunku
do macierzy podatności, i:
′
′
C
r−
1 , P
() ξ = −lr
⋅lr
ω()
ξ , C
r , P
() ξ = −lr
⋅lr
ω()
ξ (dla obciążenia siłą
skupioną P=1).
r
Politechnika Poznańska®
Kopacz, Łodygowski, Pawłowski, Płotkowiak, Tymper

W YKŁ ADY Z MECHANIKI BUDOWLI
ROZWIĄZYWANIE BELEK WIELOPRZĘSŁOWYCH STATYCZNIE NIEWYZNACZALNYCH
6
Rysunek poniżej pokazuje nam linie wpływu nadliczbowych
(rys.1.6).
Rys.1.6
Politechnika Poznańska®
Kopacz, Łodygowski, Pawłowski, Płotkowiak, Tymper