Regresní analýza
Regresní analýza
Regresní analýza
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
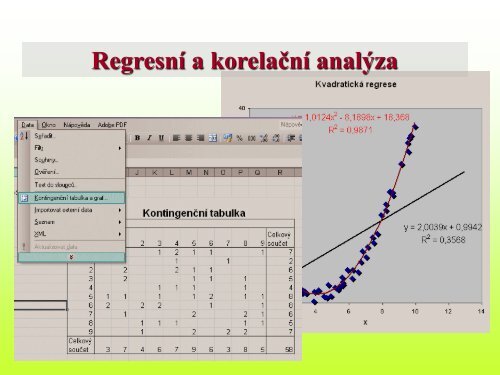
<strong>Regresní</strong> a korelační <strong>analýza</strong>
Závislost příčinná (kauzální).<br />
Závislostí pevnou se označuje případ, kdy výskytu jednoho jevu nutně<br />
odpovídá výskyt druhé jevu (a často i naopak). Z pravděpodobnostního<br />
hlediska jde o vztah, který se projeví s jistotou. Průběh závislosti (v určitém<br />
intervalu) lze přesně charakterizovat určitou matematickou funkcí.<br />
Volná závislost je závislost, při níž jeden jev podmiňuje jev jiný jen s<br />
určitou pravděpodobností a v různé intenzitě. Určité hodnotě jedné veličiny<br />
odpovídá celá řada různých hodnot druhé veličiny. U této závislosti lze<br />
charakterizovat teoretický průběh závislosti a její těsnost.<br />
<strong>Regresní</strong> <strong>analýza</strong> se zabývá jednostrannými závislostmi. Jedná se o situaci, kdy<br />
proti sobě stojí vysvětlující (nezávisle) proměnná v úloze „příčin“ a vysvětlovaná<br />
(závisle) proměnná v úloze „následků“.<br />
Korelační <strong>analýza</strong> se zabývá vzájemnými (většinou lineárními) závislostmi, kdy<br />
se klade důraz především na intenzitu (sílu) vzájemného vztahu než na zkoumání<br />
veličin ve směru příčina – následek.
Dvourozměrné rozdělení četnosti<br />
(x,y) = 0.0<br />
6<br />
4<br />
2<br />
y<br />
0<br />
-2<br />
-4<br />
-6<br />
-6 -4 -2 0 2 4 6<br />
x
Kontingenční (korelační) tabulka<br />
• Řádek korelační tabulky obsahuje rozdělení četností znaku Y za<br />
podmínky, že znak X nabyl určité konkrétní hodnoty (příp. hodnot určitého<br />
intervalu). - podmíněné rozdělení četností znaku Y.<br />
Součtový řádek – nepodmíněné rozdělení četností znaku Y.<br />
•Sloupec korelační tabulky obsahuje rozdělení četností znaku X za<br />
podmínky, že znak Y nabyl určité konkrétní hodnoty (hodnot z určitého<br />
intervalu), - podmíněné rozdělení četností znaku X.<br />
•Součtový sloupec – nepodmíněné rozdělení četností znaku X.<br />
Četnosti v součtovém řádku a součtovém sloupci nazýváme okrajovými<br />
(marginálními) četnostmi.
Příklad 1<br />
Při sledování tělesné výšky chlapců byl vysloven předpoklad, že výška dítěte je<br />
do značné míry ovlivněna výškou rodičů. Následné šetření bylo provedeno<br />
celkem u 45 chlapců a jejich otců. Z výsledků šetření byla sestavena korelační<br />
tabulka pro znaky „výška otce v cm (X)“ a „výška syna v cm (Y)“:<br />
Y<br />
170 – 174,9 175 – 179,9 180 – 184,9 185 – 189,9<br />
X<br />
190 a více n i.<br />
164 – 168,9 2 1 3<br />
169 – 173,9 2 2 3 1 8<br />
174 – 178,9 2 3 8 1 1 15<br />
179 – 183,9 3 6 9<br />
184 – 188,9 3 5 8<br />
189 a více 1 1 2<br />
n .j 6 6 11 14 8 45
Výška syna (cm)<br />
Příklad 1<br />
205<br />
200<br />
195<br />
190<br />
185<br />
180<br />
175<br />
170<br />
165<br />
160<br />
Bodový korelační graf pro znázornění závislosti mezi<br />
výškou otce a výškou syna<br />
160 165 170 175 180 185 190 195<br />
Výška otce (cm)
Postup při stanovení nejvhodnější funkce<br />
logické posouzení daného vztahu – které proměnné a funkce přicházejí v<br />
úvahu, využití zkušeností z podobných analýz apod.<br />
vytvoření bodového korelačního grafu (scatter plot)<br />
jako nejvhodnější zvolíme tu funkci, která má nejvyšší hodnotu<br />
koeficienty determinace, příp. lze využít dalších matematickostatistických<br />
kritérií (F test).
Výška syna (cm)<br />
Lineární regrese<br />
Metoda nejmenších čtverců<br />
Parametry funkce hledáme tak, aby součet čtverců chyb e i byl minimální.<br />
Pro danou regresní funkci tento součet nazýváme reziduální součet čtverců.<br />
205<br />
200<br />
195<br />
190<br />
185<br />
180<br />
175<br />
170<br />
165<br />
160<br />
Bodový korelační ngraf pro n znázornění závislosti mezi<br />
2<br />
2<br />
Svýškou otce a výškou <br />
rez<br />
ei<br />
( yi<br />
yi<br />
) min. syna<br />
i1<br />
i1<br />
y<br />
a <br />
<br />
<br />
x ,<br />
i<br />
y i<br />
x ,<br />
<br />
i<br />
y i<br />
<br />
<br />
e i<br />
i<br />
bx i<br />
160 165 170 175 180 185 190 195
Lineární regrese y=b 1 x+b 0<br />
Z podmínky minimálnosti čtverců jsou vyvozeny normální rovnice, ze<br />
kterých se jejich řešením vypočtou neznámé parametry b 1 a b 0 .<br />
b<br />
1<br />
cov( xy , )<br />
<br />
var( x)<br />
Výběrový lineární korelační koeficient<br />
S<br />
S<br />
xy<br />
xx<br />
b0 y b1<br />
x<br />
n<br />
1<br />
cov( x, y)<br />
xi<br />
x yi<br />
y<br />
n 1<br />
i1<br />
<br />
Root MeanSquareError:<br />
RMSE<br />
<br />
n<br />
<br />
i1<br />
Y<br />
2<br />
i<br />
Y<br />
i<br />
n
Reziduální a regresní součet čtverců<br />
Reziduální součet čtverců (MSE* n)<br />
<strong>Regresní</strong> součet čtverců odchylek predikcí od průměru<br />
S<br />
rez<br />
<br />
n<br />
<br />
i1<br />
S<br />
e<br />
reg<br />
2<br />
i<br />
n<br />
( y<br />
i1<br />
n<br />
( y<br />
i<br />
<br />
i1<br />
i<br />
y)<br />
i<br />
y)<br />
2<br />
2<br />
Celkový součet = součet čtverců odchylek dat od průměru<br />
S<br />
yy<br />
<br />
n<br />
( y<br />
i1<br />
i<br />
<br />
y)<br />
2<br />
<strong>Regresní</strong> identita<br />
Koeficient determinace<br />
R<br />
S<br />
2<br />
yy<br />
<br />
<br />
S<br />
S<br />
S<br />
reg<br />
yy<br />
reg<br />
S<br />
rez<br />
S<br />
1<br />
S<br />
rez<br />
yy<br />
Mean Squared Error = S rez /n<br />
Root Mean Squared Error<br />
RMSE <br />
S rez<br />
n
Výška syna (cm)<br />
200<br />
Korelační pole pro závislost výšky syna na výšce otce<br />
195<br />
190<br />
185<br />
180<br />
175<br />
y = 0,573x + 80,178<br />
170<br />
165<br />
160<br />
160 165 170 175 180 185 190 195 200 205<br />
Výška otce (cm)
y<br />
Interval spolehlivosti pro predikci<br />
Pás spolehlivosti<br />
Lineární regrese y=2x<br />
y = 2,0072x + 2,3778<br />
R 2 = 0,6973<br />
10<br />
8<br />
6<br />
4<br />
2<br />
0<br />
-2 -2 -1 -1 0 1 1 2 2<br />
-2<br />
-4<br />
-6<br />
x
Lineární regrese v Matlabu<br />
10<br />
y=b(1)*x+b(2)<br />
9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
n=100;<br />
x=randn(n,1); y=2*x+randn(n,1)/2+3; % data<br />
scatter(x,y,50,'g','filled')<br />
[R,P]=corr(x,y); % lin. korelace, p-value,<br />
2<br />
1<br />
0<br />
0 0.5 1 1.5 2 2.5 3 3.5 4<br />
[b,bint,r,rint,stats]=regress(y,[x,ones(n,1)]);<br />
% stats: R^2, F statistics, p-value,<br />
refline(b)<br />
fprintf('R^2 %1.3g \n',stats(1))<br />
fprintf('p-hodnota = %1.3g \n',stats(3)) %
Residuals<br />
Lineární regrese v Matlabu<br />
rcoplot(r,rint)<br />
2<br />
Residual Case Order Plot<br />
1.5<br />
1<br />
0.5<br />
0<br />
-0.5<br />
-1<br />
-1.5<br />
-2<br />
10 20 30 40 50 60 70 80 90 100<br />
Case Number
Lineární regrese v Matlabu<br />
polytool(x,y,1)<br />
8<br />
6<br />
4<br />
2<br />
0<br />
-2<br />
-4<br />
-2 -1.5 -1 -0.5 0 0.5 1 1.5
Robustní lineární regrese v Matlabu<br />
robustdemo(x,y);<br />
[b_r,stats_r]=robustfit(x,y)<br />
Use left mouse button to select and drag points<br />
Use right mouse button to query point properties<br />
8<br />
7<br />
6<br />
5<br />
4<br />
S<br />
rez<br />
<br />
n<br />
<br />
i1<br />
e<br />
2<br />
i<br />
( y<br />
i1<br />
Mean Squared Error = S rez /n<br />
Root Mean Squared Error<br />
n<br />
i<br />
y)<br />
i<br />
2<br />
yLeast 3<br />
squares<br />
Robust<br />
2<br />
1<br />
0<br />
-1<br />
-2<br />
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5<br />
x<br />
RMSE<br />
<br />
S rez<br />
n<br />
Least squares:<br />
Robust:<br />
Y = 2.95067 + 1.94112*X<br />
Y = 2.9483 + 1.94524*X<br />
RMS error = 0.520848<br />
RMS error = 0.534759
Nelineární regrese
Nelineární regrese<br />
Funkci hledám v předepsaném tvaru (exponenciální, polynomiální,…)<br />
parametry nalezneme metodou nejmenších čtverců<br />
Koeficient determinace R 2 – popisná míra vhodnosti použití regresní<br />
rovnice pro predikování. Hodnoty blízké nule naznačují, že zvolená<br />
funkce není vhodná. Naopak, hodnoty blízké 1 naznačují, že rovnice je<br />
velmi vhodná pro extrapolaci.<br />
Malá hodnota ale nemusí znamenat nízký stupeň závislosti mezi<br />
proměnnými, ale může signalizovat špatně zvolenou regresní funkci<br />
R<br />
<br />
N<br />
<br />
2 i1<br />
N<br />
<br />
i1<br />
<br />
<br />
y y<br />
y<br />
i<br />
i<br />
<br />
y<br />
<br />
<br />
2<br />
2<br />
R<br />
2<br />
<br />
S<br />
S<br />
reg<br />
yy<br />
S<br />
1<br />
S<br />
rez<br />
yy<br />
Mean Squared Error = S rez /n<br />
Root Mean Squared Error<br />
RMSE<br />
<br />
S rez<br />
n<br />
S<br />
rez<br />
<br />
n<br />
<br />
i1<br />
e<br />
2<br />
i<br />
<br />
n<br />
( y<br />
i1<br />
i<br />
<br />
y)<br />
i<br />
2
Korelace náhodných proměnných<br />
6<br />
(x,y) =<br />
0.0<br />
0.0 (x,y) = 0.7<br />
6<br />
(x,y) = 0.7<br />
4<br />
4<br />
2<br />
2<br />
y<br />
0<br />
y<br />
0<br />
-2<br />
-2<br />
-4<br />
-4<br />
-6<br />
-6 -4 -2 0 2 4 6<br />
-6<br />
-6 -4 -2 0 2 4 6<br />
x<br />
x<br />
N = 10000
Korelace náhodných proměnných<br />
(x,y) (x,y) = -0.7 = - (x,y) (x,y) = = 0.96<br />
6<br />
6<br />
4<br />
4<br />
2<br />
2<br />
y<br />
0<br />
y<br />
0<br />
-2<br />
-2<br />
-4<br />
-4<br />
-6<br />
-6 -4 -2 0 2 4 6<br />
-6<br />
-6 -4 -2 0 2 4 6<br />
x<br />
x<br />
N = 10000
Korelace náhodných proměnných
Nelineární regrese v Excelu<br />
Graf > přidat spojnici trendu<br />
koeficient spolehlivosti R 2 je<br />
koeficient determinace
Nelineární regrese v Excelu<br />
Graf > přidat spojnici trendu<br />
koeficient spolehlivosti R 2 je<br />
koeficient determinace<br />
2<br />
R <br />
S<br />
S<br />
reg<br />
yy
y<br />
Nelineární regrese v Matlabu<br />
10<br />
y=b(1)*x 2 +b(2)*x+b(3)<br />
9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
x=randn(100,1);<br />
y=x.^2 + 3 + randn(100,1)/2;<br />
scatter(x,y,50,'g','filled')<br />
b=polyfit(x,y,2);<br />
refcurve(b)<br />
0<br />
-3 -2 -1 0 1 2 3<br />
x
Nelineární regrese v Matlabu<br />
polytool(x,y,2)<br />
14<br />
12<br />
10<br />
8<br />
6<br />
4<br />
2<br />
0<br />
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5
y<br />
Nelineární regrese v Matlabu<br />
func=@(a,x)(a(1)*x.^2+a(2)*x+a(3));<br />
9<br />
a0=[1;0;3];<br />
ahat=nlinfit(x,y,func,a0);<br />
%graf<br />
xrange = min(x):.02:max(x);<br />
7<br />
hold on<br />
scatter(x,y)<br />
6<br />
plot(xrange,func(ahat,xrange),'m')<br />
hold off<br />
10<br />
8<br />
5<br />
nlinfit: @(a,x)(a(1)*x. 2 +a(2)*x+a(3));<br />
4<br />
3<br />
2<br />
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3<br />
x
Nelineární regrese v Matlabu<br />
nlintool(x,y,func,a0)<br />
10<br />
9<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
-2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2
Testy korelační analýzy<br />
Kontingenční tabulky umožňují testování různých statistických<br />
hypotéz:<br />
– hypotéza o nezávislosti znaků - oba znaky se vzájemně<br />
neovlivňují (výška rodičů nemá vliv na výšku dětí)<br />
– hypotéza o shodnosti struktury (homogenitě) - očekávané<br />
četnosti jsou v políčcích každého řádku ve stejném vzájemném<br />
poměru bez ohledu na konkrétní volbu řádku (rozložení výšky je<br />
stejné u otců i u synů)<br />
Klasický test nezávislosti nebo homogenity je založen na testu dobré<br />
shody, tedy porovnání očekávaných četností v jednotlivých políčcích<br />
tabulky za předpokladu, že hodnoty obou sledovaných znaků na sobě<br />
nezávisí, a skutečných četností
Chí-kvadrát test v Excelu<br />
H 0 – náhodné výběry pocházejí ze stejného rozdělené<br />
CHITEST(aktuální;očekávané)<br />
aktuální četnosti – získáné použitím funkce<br />
četnosti(data, hodnoty).<br />
očekávané jak by četnosti vypadaly pro teoretické rozdělení – sestejným<br />
počtem pozorování a stejnými hodnotami.<br />
funkce CHITEST vrací p-hodnotu. Pro p
Testování lineární regrese<br />
T test korelačního koeficientu (Pearsonův test)<br />
H 0 : data nejsou vhodná k lineární regresi<br />
t_test_reg.m<br />
F test poměru vysvětleného a nevysvětleného rozptylu<br />
H 0 : data nejsou vhodná k lineární regresi<br />
f_test_reg.m<br />
y<br />
<br />
kx<br />
q<br />
=LINREGRESE(pole_y;pole_x;PRAVDA;PRAVDA)<br />
=INTERCEPT(pole_y;pole_x)<br />
=SLOPE(pole_y;pole_x)<br />
absolutní člen q<br />
směrnice k
y<br />
Kvadratická regrese<br />
Koeficient determinace<br />
10<br />
9<br />
y = 1,9733x 2 - 0,0103x + 0,5794<br />
R 2 = 0,9898<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
0<br />
-2 -2 -1 -1 0 1 1 2 2<br />
x<br />
Srez 3,617<br />
Sreg 349,6751 `=VAR(f(x))*n<br />
průměr y 2,829 2,829<br />
Sxx 56,75074 `=VAR(x)*n<br />
Celkový součet čtverců Syy 353,3079 353,292 =Srez+Sreg `=VAR(y)*n<br />
Reziduální rozptyl Se 0,075357 =Srez/(n-2)<br />
Koeficient determinace R2 0,989762 0,04605 =Sreg/(Srez+Sreg) `=R^2<br />
Pearsonův korel. Koeficient R -0,214597 -0,2146 ´=PEARSON(data_x;data_y)
F test poměru vysvětleného a nevysvětleného<br />
rozptylu<br />
H0: Data nejsou vhodná pro regresi<br />
F<br />
<br />
( n 2) Sreg<br />
Srez<br />
<br />
F(1,<br />
n 2)<br />
pravostranný test<br />
p<br />
hodnota<br />
<br />
P F <br />
F<br />
0<br />
<br />
LINREGRESE y=kx+q<br />
směrnice k, q 2,7158689 7,534689<br />
st.chyba koeficientů 0,4244274 0,749496<br />
Koef. Determinace R2,st. Chyba odhadu y 0,4603464 5,245447<br />
F statistika, df 40,945939 48<br />
regresni a rezidualni součet čtverců<br />
Sreg, Srez<br />
1126,6159 1320,706
Korelační <strong>analýza</strong> ordinálních veličin<br />
Je důležité odlišit případy, kdy je ordinálního charakteru pouze jedna<br />
proměnná a kdy obě.<br />
V případech, kdy jsou obě sledované proměnné ordinálního<br />
charakteru, můžeme použít testování, založené na pořadí.<br />
– Wilcoxonův test<br />
– Mann-Whitney test<br />
– Kendallův korelační koeficient τk - tau k<br />
– Goodman-Kruskalův koeficient γ je variantou kendallova τk<br />
Pokud je ordinální jen jedna, pak:<br />
– Kruskal-Wallisův test