Završni ispit iz predmeta Kvantna mehanika I ZADACI - PMF

Univerzitet u Sarajevu
Odsjek za fiziku, Prirodno-matematički fakultet
Završni ispit iz predmeta Kvantna mehanika I
15.01.2013. godine
ZADACI
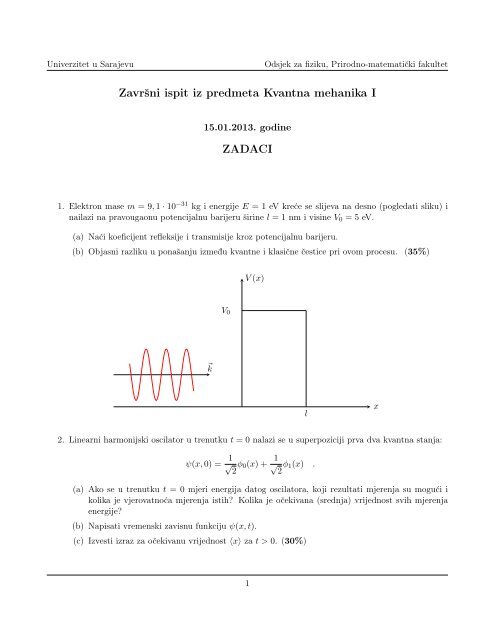
1. Elektron mase m = 9, 1 · 10 −31 kg i energije E = 1 eV kreće se slijeva na desno (pogledati sliku) i
nailazi na pravougaonu potencijalnu barijeru širine l = 1 nm i visine V 0 = 5 eV.
(a) Naći koeficijent refleksije i transmisije kroz potencijalnu barijeru.
(b) Objasni razliku u ponašanju između kvantne i klasične čestice pri ovom procesu. (35%)
V (x)
⃗ k
V 0
l
x
2. Linearni harmonijski oscilator u trenutku t = 0 nalazi se u superpoziciji prva dva kvantna stanja:
ψ(x, 0) = 1 √
2
φ 0 (x) + 1 √
2
φ 1 (x) .
(a) Ako se u trenutku t = 0 mjeri energija datog oscilatora, koji rezultati mjerenja su mogući i
kolika je vjerovatnoća mjerenja istih? Kolika je očekivana (srednja) vrijednost svih mjerenja
energije?
(b) Napisati vremenski zavisnu funkciju ψ(x, t).
(c) Izvesti izraz za očekivanu vrijednost 〈x〉 za t > 0. (30%)
1

Univerzitet u Sarajevu
Odsjek za fiziku, Prirodno-matematički fakultet
3. Elektron mase m nalazi se u trodimenzionalnoj kutiji čija je dužina ivice jednaka a:
{ 0 0 ≤ x ≤ a, 0 ≤ y ≤ a, 0 ≤ z ≤ a
V (x, y, z) =
∞ inače
(a) Odrediti ortonormirane talasne funkcije elektrona kao i dozvoljene energije.
(b) Odrediti stepen degeneracije za prva četiri energetska nivoa. (35%)
Pomoćni izrazi:
Tablični ∫ integral:
∞
√
x 2n (2n − 1)!! π
e −px2 dx =
0
2(2p) n p
Vlastite funkcije √ linearnog harmonijskog oscilatora:
( λ
φ 0 (x) = 4 π exp − 1 )
2 λx2 √
√ (
1 λ
φ 1 (x) = 2
2 π exp − 1 ) √λx mω
2 λx2 , λ =
2

Univerzitet u Sarajevu
Odsjek za fiziku, Prirodno-matematički fakultet
Rješenje:
1. Pogledati bilješke sa auditornih vježbi.
2. (a) Oscilator se nalazi u superpozicija prva dva kvantna stanja tako da su moguće vrijednosti
izmjerene energije jednake E 0 = 1 2 ω i E 1 = 3 ω. Vjerovatnoća mjerenja datih energija je
2
određena kvadratima modula linearnih koeficijenata a 0 = √ 1 i a 1 = √ 1 . Prema tome, postoji
2 2
podjednaka vjerovatnoća da u eksperimentu izmjerimo energiju E 0 i E 1 i ona iznosi w = 50%.
S druge strane, srednja vrijednost energije svih mjerenja je data izrazom:
〈E〉 = ∑ i
|a i | 2 E i = 1 2 ω + 1 3
ω = ω .
2 2
(b) Vremenski zavisna talasna funkcija ψ(x, t) je data sa
ψ(x, t) = ∑ (
a i φ i (x) exp − i )
E it = √ 1 φ 0 (x) exp
i
2
(− i 2 ωt )
+ 1 √
2
φ 1 (x) exp
(
− 3i
2 ωt )
.
(c) Očekivana vrijednost 〈x〉:
〈x〉 =
+ 1 2
∫ ∞
−∞
ψ ∗ (x, t)xψ(x, t)dx = 1 2
∫ ∞
−∞
∫ ∞
−∞
φ 2 0xdx + 1 2
∫ ∞
−∞
φ 0 φ 1 xdx [exp(−iωt) + exp(iωt)] = cos(ωt)
φ 2 1xdx
∫ ∞
−∞
φ 0 φ 1 xdx
Prva dva integrala su jednaka nuli jer je podintegralna funkcija neparna, a interval integracije
simetričan, tako da je tražena očekivana vrijednost jednaka
√ √
λ
〈x〉 = 2 cos(ωt) 4 4 λ √
∫ ∞
λ exp ( √
−λx 2)
x 2 dx =
2π π
2mω cos(ωt) ,
−∞
gdje smo u posljednjem koraku iskoristili dati tablični integral.
3. (a) Schrödingerova jednačina koja opisuje datu česticu je data sa
( )
− 2 ∂
2
2m ∂x 2 + ∂2
∂y 2 + ∂2
∂z 2 Ψ(x, y, z) = EΨ(x, y, z) .
Varijable su međusobno separabilne tako rješenje možemo napisati u obliku Ψ(x, y, z) =
φ(x)η(y)ξ(z). Nakon uvrštavanja dobijamo diferencijalne jednačine
d 2 φ
dx 2 + a2 φ = 0 , a 2 = 2mE 1
2 ,
d 2 η
dy 2 + b2 φ = 0 , b 2 = 2mE 2
2 ,
d 2 ξ
dz 2 + c2 φ = 0 , c 2 = 2mE 3
2 ,
3

Univerzitet u Sarajevu
Odsjek za fiziku, Prirodno-matematički fakultet
uz uslov E = E 1 + E 2 + E 3 . Opšta rješenja diferencijalnih jednačina su
φ = A 1 sin(ax) + A 2 cos(ax) ,
η = B 1 sin(by) + B 2 cos(by) ,
ξ = C 1 sin(cz) + C 2 cos(cz) .
Zbog graničnih uslova φ(0) = φ(a) = 0, η(0) = η(a) = 0 i ξ(0) = ξ(a) = 0, dobijamo
( n1 π
)
φ(x) = A 1 sin
a x ,
( n2 π
)
η(y) = B 1 sin
a y ,
( n3 π
)
ξ(z) = C 1 sin
a z .
Ukupna energija elektrona je
Totalna talasna funkcije je
E n1 n 2 n 3
= π2 2 (
n
2
2ma 2 1 + n 2 2 + n 2 )
3
Ψ(x, y, z) =
, n 1 , n 2 , n 3 = 1, 2, 3, . . .
√
8
(
a 3 sin n1 π
) (
a x n2 π
) (
sin
a y n3 π
)
sin
a z
gdje smo konstatnu normiranja C = A 1 B 1 C 1 odredili iz uslova ortonormiranosti talasne funkcije
Ψ(x, y, z).
(b) Osnovno stanje ima najnižu moguću energiju E 111 = 3 π2 2
i ovo stanje nije degenerisano jer
2ma2 samo jedno jedna kombinacija kvantnih brojeva daje datu energiju. Sljedeći energetski nivo
ima nešto višu energiju i njega čine kvantna stanja (121), (112) i (211)
E 112 = E 212 = E 221 = 6 π2 2
2ma 2 .
Stepen degeneracije drugog energetskog nivoa je g 2 = 3.
Treći energetski nivo čine kvantna stanja (221), (212) i (122):
E 221 = E 212 = E 122 = 9 π2 2
2ma 2 .
Dakle, stepen degeneracije trećeg energetskog nivoa je g 3 = 3. Četvrti energetski nivo je takođe
trostruko degenerisan jer ga čine kvantna stanja (113), (131), (311):
E 113 = E 131 = E 311 = 11 π2 2
2ma 2 .
,
4