Przemieszczenia układów statycznie wyznaczalnych 8

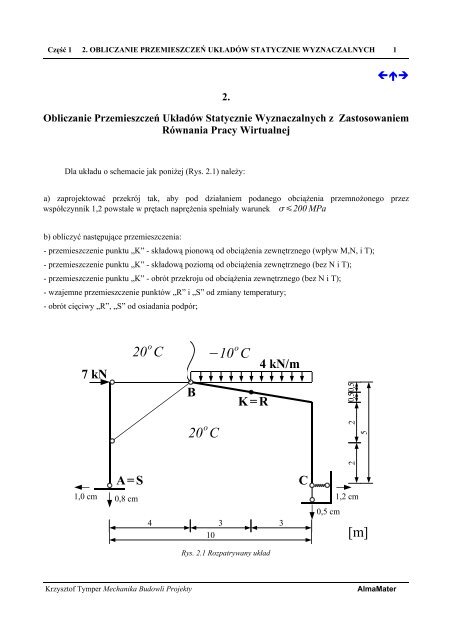
,200 MPa20 o C 10 o C20 o CRys. 2.1 Rozpatrywany układMechanika Budowli ProjektyAlmaMater

Warunek projektowy:gdzie:dop (2.2.1)dop 200 MPa 200 10 6 Pa 20 10 6 N m 2 200 10 3 kN m 2 (2.2.2)M eksWkN mm 3kNm 2 10−3 MPa (2.2.3)Przekształcając powyŜsze równanie (2.2.3) otrzymamy wzór na potrzebny wskaźnik wytrzymałości (2.2.5):W M eks kN mkN m 2 m 3 (2.2.4)a po uwzględnieniu znalezionej wcześniej (Rys.2.1.1) maksymalnej wartości momentu zginającegoM eks :M eks 39,84 kN m (2.2.5)oraz po uwzględnieniu warunku projektowego (2.2.1) i warunku z treści zadania, otrzymamy:1,2 39,84W 0,00023904 m 3 239,04 cm 3200 10 3 (2.2.6)Na podstawie uzyskanego powyŜej wskaźnika (2.2.6), z tablic konstrukcji stalowych, przyjęto przekrójdwuteowy I 220 o następujących parametrach:W x 278 cm 3 0,000278 m 3 278 10−6 m 3J x 3060 cm 4 0,0000306 m 4 3060 10−8 m 4A 39,6 cm 2 0,00396 m 2 39,6 10−4 m 2 (2.2.7)a następnie dokonano sprawdzenia warunku projektowego (2.2.1)1,2 39,84 10027817,197 kNcm 2 171,97 MPa171,97 200(2.2.8)Spełnienie powyŜszej nierówności jest równoznaczne z poprawnym przyjęciem przekroju.Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

a) dla prętów zginanych (I 220):E=205 [GPa ]=205⋅10 9 [ Pa ]=205⋅10 9[ N m 2] =205⋅106[ kN m 2 ]J x =3060 [cm 4 ]=0,0000306 [m 4 ]=3060⋅10 −8 [m 4 ]A=39,6 [cm 2 ]=0,00396 [m 2 ]=39,6⋅10 −4 [m 2 ]h=220 [mm]=22,0 [cm]t w =8,1 [mm]=0,81 [cm]=0,3 [−]=0,2 [m −3 ]G= E21 = 205⋅106210,3 [ =78846153,85 kN /m2− = kN m ] 2= A A śr= At w ⋅h = 39,60,81⋅22 =2,222 [ cmcm =− ]E⋅J =205⋅10 6 ⋅3060⋅10 −8 =6273,0 [ kN m 2⋅m4 =kN⋅m 2]G⋅A=78846153,85⋅39,6⋅10 −4 =312230,77 [ kN m=kN]2⋅m2E⋅A=205⋅10 6 ⋅39,6⋅10 −4 =811800,0 [ kN m=kN]2⋅m2(2.3.1.1)k=⋅E J =0,2⋅6273,0=1254,6[ 1 m 3⋅kN⋅m2 = kN m ](2.3.1.2)b) pręty obciąŜone wyłącznie siłą osiową (normalną)E=205 [GPa ]=205⋅10 9 [ Pa ]=205⋅10 9[ N m 2] =205⋅106[ kN m 2 ]A=2,86 [cm 2 ]=0,000286 [m 2 ]=2,86⋅10 −4 [m 2 ]E⋅A=205⋅10 6 ⋅2,86⋅10 −4 =58630 [ kN m 2⋅m2 =kN](2.3.1.3)Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

√372 2 0,50,55k4 3 310[m]Rys. 2.3.2.1 Rozpatrywany układ obciąŜony jedynkową siłą wirtualnąPrzemieszczenia wyliczymy korzystając z równania pracy wirtualnej (2.3.2.1).Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

N NEA dxT TGA dxM MEJ dx nR R 1xxxk(2.3.2.1)kNkN m 2 m m m , kN2kN m 2 m m m , kN m m2kN m 2 m m m , kN4 kN m mPowyŜsze równanie (2.3.2.1) a konkretniej rzecz ujmując całkowanie wykresów sił wewnętrznych,wykonamy korzystając z twierdzenia Mohra-Wiereszczagina (2.3.2.2).K1811800,0158630,00,3 2 3,70 0,18737 1379,216 11,189 0,3522 2 211,189 13,162 0,70 4 20,300,5 5 6,167 0,16 4 5,026122,222312230,770,24 2 2,96 0,16 3 1,974 0,335 37237 16,550 18,386 0,24 4 9,9602 2125,287 6,550 0,65116273,05,92 223722 5,92 30,483 21,92 3712 1,02 2213 1,02 2 3 0,96 4 3 281,92 3723 0,48 222 4 321,023 823 1,02 1 39,84 373 0,96 22233722312 1,02 0,96 39,84 4223 0,96(2.3.2.2)9,96 0,241254,677,897231811800,012,2008658630,00,096 0,208 0,256 12,083 1,905 10−32,222 35,97239312230,770,0145 m75,7970176273,02,39041254,6Uzyskany powyŜej wynik (2.3.2.2) to poszukiwane pionowe przemieszczenie punktu „K”. Warto tutajzwrócić uwagę na udział poszczególnych wpływów na wielkość tego przemieszczenia:- siły normalne (ściskanie, rozciąganie): - siły tnące (ścinanie):0,096 0,2080,256KN100 2,09KT 100 1,76 (2.3.2.3)14,54814,548- momenty zginające (zginanie): - charakterystyka konstrukcji (podatność podpory):K M 12,08314,548 100 83,06 1,905K k 100 13,09 (2.3.2.4)14,548Jak widać z powyŜszego (2.3.2.3 i 2.3.2.4) największy wpływ na przemieszczenie rozpatrywanego punktuma działanie momentu zginającego (zginania) oraz podatność jednej z podpory rozpatrywanej konstrukcjiKrzysztof Tymper Mechanika Budowli ProjektyAlmaMater

(razem 96,15%), zaś wpływ pozostałych sił wewnętrznych (3,85%) w elementach zginanych jest dopominięcia.√372 2 0,50,55k4 3 310[m]Rys. 2.3.3.1 Rozpatrywany układ obciąŜony jedynkową siłą wirtualnąPrzemieszczenie wyliczymy korzystając z równania pracy wirtualnej (2.3.3.1).M MxEJ dx N NxEA dx R R 1n k(2.3.3.1)kN m mkN m 2 m m m , kN4kN m 2 m m m , kN2 kN m mPowyŜsze równanie (2.3.3.1) a konkretniej rzecz ujmując całkowanie wykresów sił wewnętrznych,Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

ponownie wykonamy korzystając z twierdzenia Mohra-Wiereszczagina (2.3.3.2), z tymŜe wpływ siłynormalnej uwzględnimy wyłącznie w prętach kratownicy.k16273,05,92 223722 5,92 30,723 21,92 3712 1,53 2213 1,53 2 3 2,56 4 3 281,92 3723 0,72 2 2 4 321,532 3 823 1,53 1 39,84 373 2,56 222337212 1,53 2,56 39,84 422323 2,56(2.3.3.2)158630,0 0,75 5 6,167 0,24 4 5,026 9,96 0,641254,6245,9873286273,018,3012958630,06,37441254,60,0440 mUzyskany powyŜej wynik (2.3.3.2) to poszukiwane poziome przemieszczenie punktu „K”.Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

√372 2 0,50,55k4 3 310[m]Rys. 2.3.4.1 Rozpatrywany układ obciąŜony jedynkowym momentem wirtualnymPrzemieszczenia wyliczymy korzystając z równania pracy wirtualnej (2.3.4.1).kN mkN m 2 m rad ,xM MEJ dx xN NEA dxnR R 1 kkN 1 mkN m 2 m m rad , kN 1 m2 kN mrad(2.3.4.1)PowyŜsze całki (2.3.4.1) wyliczymy analogicznie jak wcześniej, tzn. korzystając z twierdzenia Mohra-Wiereszczagina (2.3.4.2).Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

16273,05,92 223722 5,92 30,163 21,92 3712 0,34 2213 0,66 2 3 0,32 4 3 281,92 3723 0,16 2 2 4 320,342 3 823 0,66 1 39,84 373 0,32 222337212 0,66 0,32 39,84 422323 0,32(2.3.4.2)158630,0 0,167 5 6,167 0,053 4 5,026 9,96 0,081254,642,8448566273,04,08393358630,00,79681254,60,0075 radUzyskany powyŜej wynik (2.3.4.2) to poszukiwany obrót przekroju w punkcie „K”.Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

20 o C 10 o Ct 0 o C ,t o 10 o C t 30 o C ,t o 5 o C20 o C√372 2 0,50,554 3 310 [m]kxRys. 2.3.5.1 Rozpatrywany układ obciąŜony parą sił jedynkowych leŜących na jednej prostejPrzemieszczenia wyliczymy korzystając z równania pracy wirtualnej (2.3.5.1).M ttmdx N tho tdxo C−1 o Cm m ,o C o C−1 m m (2.3.5.1)mgdzie:- t t dt gx- t ot d t g2- t m 10 o Ct m-t 1,2 10−5 o C−1- h 220 mm 0,22 mPowyŜsze całki (2.3.5.1) wyliczymy analogicznie jak wcześniej, tzn. korzystając z twierdzenia Mohra-Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater

Wiereszczagina (2.3.5.2).R−S1,838 371,220,22 10 5 20,864 221,838 37220,864 3201,634 37221,634 4230(2.3.5.2)1,2 10−50,541 2 0,901 5 0,289 4 10 0,3373720,40337251856,10 54,38 10−51801,72 10−50,0180 mUzyskany powyŜej wynik (2.3.5.2) to poszukiwane wzajemne przemieszczenie punktów „R” i „S”.√69,25√371√69,25[-]2 2 0,50,551,0 cm k1 1,2 cm0,8 cm [-]√69,250,5 cm4 3 310[m]Rys. 2.3.6.1 Rozpatrywany układ obciąŜony parą sił jedynkowych leŜących na jednej prostejPrzemieszczenia wyliczymy korzystając z równania pracy wirtualnej (2.3.6.1).nR m m (2.3.6.1)Po podstawieniu konkretnych wartości do powyŜszego równania (2.3.6.1) otrzymamy:R−S0,066 0,01 0,1 0,008 0,066 0,012 0,1 0,005 0,0011 m (2.3.6.2)Uzyskany powyŜej wynik (2.3.6.2) to poszukiwany obrót cięciwy „R”, „S”.Krzysztof Tymper Mechanika Budowli ProjektyAlmaMater