DERIVACE FUNKCE

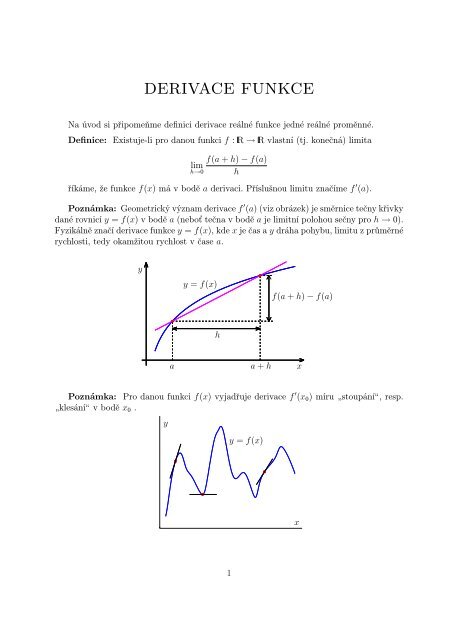
Uvedené vzorce jsou pro výpočet první derivace f ′ (x 0 ), pro výpočet druhé derivacef ′′ (x 0 ) můžeme použít například vzorec, který dostaneme po sečtení vztahů:f(x 0 + h) = f(x 0 ) + hf ′ (x 0 ) + h22 f ′′ (x 0 ) + h36 f ′′′ (x 0 ) + h424 f (4) (ξ 1 ), ξ 1 ∈ (x 0 , x 0 + h)f(x 0 − h) = f(x 0 ) − hf ′ (x 0 ) + h22 f ′′ (x 0 ) − h36 f ′′′ (x 0 ) + h424 f (4) (ξ 2 ), ξ 2 ∈ (x 0 − h, x 0 )f(x 0 + h) + f(x 0 − h) = 2f(x 0 ) + h22 f ′′ (x 0 ) + h424 (f (4) (ξ 1 ) + f (4) (ξ 2 ))Odtud vyjádříme druhou derivaci a získáme tříbodový vzorec pro druhou derivacif ′′ (x 0 ) = f(x 0 + h) − 2f(x 0 ) + f(x 0 − h)h 2− h224 (f (4) (ξ 1 ) + f (4) (ξ 2 ))} {{ }O(h 2 )Poznámka: Samozřejmě lze odvodit řadu dalších vzorců, přičemž platí, že čím vícebodů použijeme, tím bude řád chyby vyšší.Příklad: Pomocí uvedených tří vzorců vypočtěte přibližnou hodnotu první derivacefunkce f(x) = e x (1 − x) v bodě x 0 = 1. Použijte krok h = 0, 1.Řešení: (Nejprve si pro kontrolu analyticky zjistíme přesnou hodnotu první derivacefunkce f bodě x 0 :f ′ (x) = e x (1 − x) + e x (−1) = −xe x , tj. f ′ (1) = −1e 1 = −e ≈ −2, 7182.)Nyní použijeme pravou, levou a centrální poměrnou diferenci:1. D P f(x 0 , h) = f(x 0 + h) − f(x 0 )= e1,1 (1 − 1, 1) − e 1 (1 − 1)h0, 1−0, 1e1,1=0, 12. D L f(x 0 , h) = f(x 0) − f(x 0 − h)−0, 1e0,9=0, 13. D C f(x 0 , h) = f(x 0 + h) − f(x 0 − h)2h= −0, 1e1,1 − 0, 1e 0,90, 2h= −e 1,1 ≈ −3, 0041 tj. chyba je přibližně 0, 2858= e1 (1 − 1) − e 0,9 (1 − 0, 9)0, 1= −e 0,9 ≈ −2, 4596 tj. chyba je přibližně 0, 2586=== e1,1 (1 − 1, 1) − e 0,9 (1 − 0, 9)0, 2= − e1,1 + e 0,9≈ −2, 73182tj. chyba je přibližně 0, 0136Všimněme si velikosti chyb v jednotlivých případech. Potvrzuje se fakt, že chyba prvníchdvou (dvoubodových) vzorců je řádu h, tj. v řádu desetin a chyba posledního (tříbodového)vzorce je řádu h 2 , tj. v řádu setin.✷4=

Podmíněnost úlohy numerického derivováníUvažujme nyní např. vzorec s pravou diferencí D P f(x 0 , h), tj. platíf ′ (x 0 ) = f(x 0 + h) − f(x 0 )h} {{ }D P f(x 0 ,h)−12 hf ′′ (ξ)} {{ }chyba metodyChybu metody označme r 1 . Platí-li |f ′′ (x)| < M pro x ∈ (x 0 , x 0 + h), potom |r 1 | ≤ M 2 h.Dále je třeba uvážit chyby měření, resp. zaokrouhlovací chyby, které označíme r 2 .Označíme-lif(x 0 ), f(x 0 + h) . . . . . . přesné hodnotyf ⋆ (x 0 ), f ⋆ (x 0 + h) . . . . . . vstupní hodnotyPotom pro r 2 platír 2 = f(x 0 + h) − f(x 0 ) f ⋆ (x 0 + h) − f ⋆ (x 0 )−} {{ h } } {{ h }přesná hodnota vzorce vypočtená hodnota vzorceA dálef(x 0 + h) − f ⋆ (x 0 + h)|r 2 | =+ f ⋆ (x 0 ) − f(x 0 )∣ hh ∣ ≤≤ |f(x 0 + h) − f ⋆ (x 0 + h)|h≤ε h + ε h = 2εh+ |f ⋆ (x 0 ) − f(x 0 )|hVyužili jsme zde odhady |f ⋆ (x 0 + h) − f(x 0 + h)| ≤ ε a |f ⋆ (x 0 ) − f(x 0 )| ≤ ε , kde čísloε může představovat např. strojovou přesnost.Pro celkovou chybu r potom platír|r| ≤ |r 1 | + |r 2 | ≤ M 2 h + 2εh≤y = M 2 h• Úloha numerického derivováníje špatně podmíněná !(pro zmenšující se h roste chyba)• Lze najít optimální krok h opth opth5

Poznámka: Na základě špatné podmíněnosti se zdá, že nebude možné při výpočtuderivace dosáhnout libovolné přesnosti. Zvýšení přesnosti ale můžeme dosáhnout1) použitím vzorce s chybou vyššího řádu2) použitím tzv. Richardsonovy extrapolaceVěnujme nyní pozornost Richardsonově extrapolaci. Je třeba zdůraznit, že se jednáo obecný princip, který se nepoužívá jen u numerického výpočtu derivace. Myšlenkavychází z toho, že na základě znalosti výrazu pro rozvoj chyby využijeme dvou přibližnýchvýsledků k získání třetího, který bude přesnější. Tento proces eliminace chyb budemedemonstrovat např. na poměrné centrální diferencif ′ (x 0 , h) = f(x 0 + h) − f(x 0 − h)2h} {{ }D C f(x 0 ,h)− h26 f ′′′ (ξ 1 ), ξ 1 ∈ (x 0 − h, x 0 + h). (1)Podobný vztah musí platit i v případě, že použijeme místo kroku h krok 2h, tj.f ′ (x 0 , 2h) = f(x 0 + 2h) − f(x 0 − 2h)2 · 2h} {{ }D C f(x 0 ,2h)− (2h)26 f ′′′ (ξ 2 ), ξ 2 ∈ (x 0 − 2h, x 0 + 2h). (2)Pro jednoduchost předpokládáme, že hodnoty f ′′′ (ξ 1 ) a f ′′′ (ξ 2 ) jsou si rovny. Vhodnoukombinací (1) a (2) dosáhneme eliminace chyby řádu h 2 , tj. od čtyřnásobku rovnice (1)odečteme rovnici (2) a výsledek dělíme třemi (4-1). Dostaneme přesnější aproximaci derivacefunkce f v bodě x 0 :f ′ (x 0 ) ≈ 4f ′ (x 0 , h) − f ′ (x 0 , 2h)3= 4 3 f ′ (x 0 , h) − 1 3 f ′ (x 0 , 2h) (3)Poznámka: V názvu metody se objevuje slovo extrapolace. Je to proto, že nováhodnota derivace je lineární kombinací dvou hodnot, ovšem neleží mezi těmito hodnotami(kdyby tomu tak bylo, mluvili bychom o interpolaci).Poznámka: Algoritmus Richardsonovy extrapolace lze samozřejmě použít opakovaněpro eliminaci chyb vyšších řádů. Tato metoda je potom velmi efektivní.Příklad: Použijte opakovanou Richardsonovu extrapolaci pro výpočet derivace funkcef(x) = ln x v bodě x 0 = 3 pomocí centrální poměrné diference s kroky h = 0, 8; 0, 4; 0, 2 a0, 1.Řešení: Dá se ukázat (viz. odvození), že pro dostetečně hladkou funkci f platí tentovztahf ′ (x 0 ) = f(x 0 + h) − f(x 0 − h)2h} {{ }D C f(x 0 ,h)+ c 1 h 2 + c 2 h 4 + c 3 h 6 + . . .,} {{ }rozvoj chybykde čísla c 1 , c 2 , c 3 představují kontanty obsahující příslušné derivace.6

Pro přehlednost budeme výsledky zapisovat do tabulky:h f ′ (x 0 , h) po 1. korekci - vztah (3) po 2. korekci - vztah (4)0, 8 0, 3415890, 4 0, 335329 4 3 0, 335329 − 1 0, 341589 =3= 0, 3332420, 2 0, 333828 4 3 0, 333828 − 1 160, 335329 =3 15 0, 333327 − 1 0, 333242 =15= 0, 333327 = 0, 3333320, 1 0, 333456 4 3 0, 333456 − 1 160, 333828 =3 15 0, 333332 − 1 0, 333327 =15= 0, 333332 = 0, 333332Ve výpočtu jsme použili jednak 1. korekci pro eliminaci chyby řádu h 2 , ale dále také2. korekci, která eliminovala chybu řádu h 4 . Vztah (4) pro 2. korekci jsme dostali podobnějako vztah (3), tj.f ′ (x 0 , h) = D C f(x 0 , h) + c 2 h 4 /· 2 4f ′ (x 0 , 2h) = D C f(x 0 , 2h) + c 2 (2h) 4/· (−1)f ′ (x 0 ) ≈ 24 f ′ (x 0 , h) − f ′ (x 0 , 2h)2 4 − 1= 1615 f ′ (x 0 , h) − 1 15 f ′ (x 0 , 2h) (4)V tabulce chybí sloupec pro 3. korekci. Důvod je ten, že se hodnoty, ze kterých by seextrapolovala nová hodnota, rovnají (dostali bychom to samé číslo). Výraz pro 3. korekcibychom opět odvodili podobně jako vztah (4), pouze místo 4 mocniny by se v něm objevila6 mocnina.Hodnota hledané derivace funkce f(x) = ln x v bodě x 0 = 3 je 0,333332. Pro úplnostdodejme, že přesná hodnota derivace je f ′ (x) = 1 x , tj. f ′ (3) = 1 3 .✷7

URČITÝ INTEGRÁL FUNKCEFormulace: Naším cílem je určit přibližnou hodnotu určitého integráluI(f) =∫ baf(x) dx,kde předpokládáme, že funkce f je na intervalu 〈a, b〉 integrovatelná.Poznámka: Geometrický význam integrálu I(f) (viz obrázek) je obsah plochy mezigrafem funkce f a osou x na intervalu 〈a, b〉.yy = f(x)abxNumerické metody výpočtu integrálu užíváme zejména tehdy, když I(f) není možnospočítat analyticky (velmi častý případ) nebo je sice analytické řešení možné, ale je velmipracné. V případě že máme zadánu funkci f tabulkou, není ani jiný přístup možný.Příklad: Chceme-li určit obsah plohy mezi grafy funkcí f a g, užijeme určitý integrál.yf(x)Sg(x)aPro obsah potom platí S =∫ baf(x) − g(x) dxbx8

Přirozený princip numerických metod pro výpočet integrálu vychází z aproximacefunkce. Danou funkci f nahradíme její vhodnou aproximací ϕ a jako aproximaci integráluI(f) prohlásíme hodnotu integrálu I(ϕ), tj.I(f) ≈ I(ϕ) =∫ baϕ(x) dx.Poznámka: Narozdíl od výpočtu derivace je výpočet integrálu stabilní, protože je-liϕ dobrou aproximací funkce f na intervalu 〈a, b〉, je integrál I(ϕ) dobrou aproximací I(f).∫ b∫ b∫ bf(x) dx − ϕ(x) dx∣ aa ∣ ≤ |f(x) − ϕ(x)| dx ≤ (b − a) sup |f(x) − ϕ(x)| .ax∈〈a,b〉} {{ }εPrincip většiny metod na výpočet určitého integráluinterval 〈a, b〉 rozdělíme na N podintervalů 〈x k , x k+1 〉 tak, že∫ ba = x 0 < x 1 < x 2 < . . . . . . < x N−1 < x N = b.af(x) dx je založen na tom, žeNa těchto podintervalech nahradíme funkci f polynomem a integrujeme tento polynom.Vzorce pro výpočet integrálu (tzv. kvadraturní vzorce) na intervalech 〈x k , x k+1 〉 budemenazývat základní a vzorec pro výpočet hodnoty integrálu přes celý interval 〈a, b〉 budemenazývat složený (složený kvadraturní vzorec je dán součtem základních kvadraturníchvzorců).Pro jednoduchost budeme předpokládat, že jsou všechny podintervaly 〈x k , x k+1 〉 stejněvelké, tj. máme tzv. ekvidistantní uzly, které můžeme vyjádřit jako x k = x 0 + kh, kdek = 0, 1, . . . , N − 1 a h = b − aN .Uveďme si nyní tři nejjednodušší základní kvadraturní vzorce, které patří mezi tzv.Newtonovy-Cotesovy kvadraturní vzorce.1) Obdélníkové pravidlo (funkci f nahrazujeme konstantní funkcí ϕ)5yf∫ xk+1x kf(x) dx ≈≈ h·f(x k + h 2 ) ≡ R Z(f, h)3210ϕx k x k+1xk + h 2−1−1 0 1 2 3 4 5 6 7x49

2) Lichoběžníkové pravidlo (funkci f nahrazujeme lineární funkcí ϕ)5yf∫ xk+1x kf(x) dx ≈≈ h 2 [f(x k) + f(x k+1 )] ≡ T Z (f, h)3210ϕx k x k+1−1−1 0 1 2 3 4 5 6 7x43) Simpsonovo pravidlo (funkci f nahrazujeme kvadratickou funkcí ϕ)5y∫ xk+2x kf(x) dx ≈≈ h 3 [f(x k) + 4f(x k+1 ) + f(x k+2 )] ≡ S Z (f, h)43210ϕ−1−1 0 1 2 3 4 5 6 7fx k x k+1 x k+2xPříklad k procvičení: Odvoďte základní vzorec pro Simpsonovo pravidlo.Poznámka: Základní vzorce v předchozím textu jsme odvodili na základě geometrickéinterpretace. V případě, že bychom chtěli vyjádřit současně i vztahy pro chyby těchtovzorců, museli bychom použít k odvození Taylorův rozvoj. Získali bychom tyto vztahy:∫ xk+1x kf(x) dx = R Z (f, h) + h324 f ′′ (ξ)∫ xk+1x k∫ xk+2x kf(x) dx = T Z (f, h) − h312 f ′′ (ξ)f(x) dx = S Z (f, h) − h590 f (IV ) (ξ)10

Příklad: Pomocí výše uvedených Newtonových-Cotesových vzorců vypočtěte integrál∫ 1,2e x dx.Řešení: (Přesné řešení je [e x ] 1,21= e 1,2 − e 1 . = 0,601835.)1R Z (e x ; 0, 2) = 0, 2e 1,1 . = 0,600833 chyba: 0,001002T Z (e x ; 0, 2) = 0, 22 (e1,0 + e 1,2 ) = . 0,603839 chyba: 0,002003S Z (e x ; 0, 1) = 0, 13 (e + 4e1,1 + e 1,2 ) = . 0,601835 chyba: 0,000000Poznámka: Všimněme si chyb. U obdélníkového pravidla vyšla chyba menší než ulichoběžníkového, přestože u lichoběžníkového pravidla jsme funkci f aproximovali „lepšífunkcí ϕ (lineární). Chyba u Simpsonova pravidla vyšla menší než u ostatních. Tyto výsledkypotvrzují vztahy pro chyby jednotlivých vzorců na minulé straně. Fakt, že obdélníkovépravidlo je přesnější než lichoběžníkové můžeme demonstrovat na obrázku:yf✷xx k xk + h 2x k+1Chceme-li získat složené kvadraturní vzorce, je třeba sečíst základní kvadraturní vzorce.Pro uvedené základní Newtonovy-Cotesovy dostaneme tyto složené kvadraturní vzorce:N−1 ∑R(f, h) ≡ h· f(x k + h 2 )k=0T (f, h) ≡ h 2 [f(x 0) + 2f(x 1 ) + 2f(x 2 ) + . . . + 2f(x N−1 ) + f(x N )] =]= h·[ 12 f(x 0) +N−1 ∑k=1f(x k ) + 1 2 f(x N)S(f, h) ≡ h 3 [f(x 0) + 4f(x 1 ) + 2f(x 2 ) + 4f(x 3 )++ . . . + 2f(x N−2 ) + 4f(x N−1 ) + f(x N )]11

Pro chyby složených vzorců potom platí:I = R(f, h) + (b − a) h224 f ′′ (ξ)I = T (f, h) − (b − a) h212 f ′′ (ξ)I = S(f, h) − (b − a) h4180 f (IV ) (ξ)Pro zpřesňování výsledků nám, stejně jako u numerického výpočtu derivace, posloužíRichardsonova extrapolace. Někdy se tato metoda také nazývá Rungeova metoda nebometoda polovičního kroku. Ukažme si nyní ještě jednou, jak se vztah pro zpřesnění odvodí:Předpokládejme, že výraz pro chybu má tvar e(f) = h k M, h = b − aN .Přesná hodnota integrálu je potomI = K(h) + h k M (5)Integrál vypočteme stejným vzorcem, ale s krokem h 2 .DostanemeDosadíme-li h k do (5), získáme( ) ( ) kh hI = K + M 12 2} {{ }ozn. ε⇒h k = ε 2kM 1(6)I = K(h) + ε 2k MM 1(5 ′ )Předpokládáme-li, že se hodnota derivace ve výrazu e(f) pro chybu příliš nemění(tj. M ≈ M 1 ), potom M M 1≈ 1 a pro (5 ′ ) a (6) musí platitK( h2)+ ε ≈ K(h) + 2 k εOdtud plyne odhad chyby εε ≈ 1 [ ( ) ]hK − K(h)2 k − 1 2a přesnější hodnota integrálu je potom( ) hI = K + 1 [ ( ) ]hK − K(h) .2 2 k − 1 212

∫ 5Příklad: Pomocí lichoběžníkového pravidla vypočtěteRichardsonovu extrapolaci.Řešení: Pro rozvoj chyby lichoběžníkového pravidla platíVýsledky opět zapíšeme do tabulkyI = T (f, h) + a 1 h 2} {{ }+ a 2 h 4} {{ }+a 3 h 6 + . . .tab. k=2 tab. k=41ln x dx. Ke zpřesnění použijteh T (f, h) 1. zpřesnění (k = 2) 2. zpřesnění (k = 4)44(ln 1 + ln 5) = 3, 2188222(ln 1 + 2 ln 3 + ln 5 =2= 3, 80663, 8066 − 3, 2188+3+ 3, 8066 = 4, 002511(ln 1 + 2 ln 2 + 2 ln 3+2+2 ln 4 + ln 5) = 3, 98273, 9827 − 3, 8066+3+ 3, 9827 = 4, 04144, 0414 − 4, 0025+15+ 4, 0414 = 4, 04399Pro kontrolu uveďme přesnou hodnotu integrálu:∫ 5u = ln x v ′ = 1∫ln x dx =1∣ u ′ = 1 5v = x= [x ln ∣ x]5 1 − dx = 5 ln 5 − 4 = . 4, 047191x✷Poznámka: Newtonovy-Cotesovy vzorce používají (m + 1) ekvidistantních uzlů a integrujípřesně polynomy až do m-tého stupně (máme na mysli základní vzorce na intervalu(x k , x k+m )). Pro zvýšení přesnosti by se mohlo zdát výhodné použít více uzlů a funkcif aproximovat polynomem vyššího řádu. Ze zkušeností z aproximace funkce polynomemovšem víme, že limitní případ polynomu stupně m → ∞ nemusí odpovídat původní funkci(říkáme, že Newton-Cotesovy vzorce nejsou konvergentní).13

Další skupinou metod pro výpočet hodnoty určitého integrálu jsou tzv. Gaussovykvadraturní vzorce. Jejich princip spočívá v tom, že se snažíme, aby kvadraturní vzorecintegroval přesně polynomy co možná nejvyššího řádu. Obecně kvadraturní vzorec budemeuvažovat ve tvarum∑K(f) = w i f(x i ),i=0kde w i jsou tzv.váhy a x i jsou uzly.Uvažujeme-li, že na základním intervalu máme m + 1 bodů, dá se ukázat, že nejvyššímožný stupeň polynomu, který se pomocí kvadraturního vzorce integruje přesně, je 2m+1(tomuto číslu říkáme algebraický řád přesnosti). U Newtonových-Cotesových vzorců bylstupeň m. Cenou za vyšší přesnost budou ovšem neekvidistantní uzly. V následujícímpříkladě je ukázán postup pro nalezení nejjednoduššího Gaussova kvadraturního vzorce.Příklad: Určete Gaussův kvadraturní vzorec pro m = 0 (tj. v intervalu uvažujemepouze jeden uzel) a pro interval 〈−1, 1〉.Řešení: Pro m = 0 má hledaný kvatraturní vzorec tvar K(f) = w 0 f(x 0 ), kde vystupují2 neznámé w 0 a x 0 . Víme, že vzorec musí přesně integrovat:∫ 1−11) konstantu2) lineární funkci(ax+b) dx =[∫ 1−1bb dx = 2b pož. { }} {= w 0 · f(x 0 ) ⇒ w 0 = 2.] 1a x22 + bx = a 2 − a 2−1 } {{ }=0+2b pož.ax 0 +b{ }} {= w 0· f(x 0 ) ⇒ 2b = 2(ax 0 +b) ⇒ x 0 = 0.Nejjednodušší Gaussůvkvadraturní vzorec je:32.521.5yfK(f) =∫ 1−1f(x) dx = 2f(0) + 1 3 f ′′ (ξ)} {{ }chyba10.50−0.5−1 0 1x−1−1.5 −1 −0.5 0 0.5 1 1.5✷14

Poznámka: Další Gaussův kvadraturní vzorec (pro m = 1) vypadá takto:∫ ( √ ) (√ )13 3K(f) = f(x) dx = f − + f + 1−13 3 135 f (IV ) (ξ) .} {{ }chybaGeometricky si jej lze představit takto:32.52yf1.510.50−0.5−1−1√1−30√1 13−1.5 −1 −0.5 0 0.5 1 1.5xPoznámka: Koeficienty a uzly vzorců vyšších řádů jsou uvedeny v tabulkách. Opětlze používat složené vzorce.Poznámka: To, že jsme vyjádřili∫ 1−1f(x) dx neubírá nic na obecnosti, můžeme totižlibovolný interval 〈a, b〉 transformovat na 〈−1, 1〉 a použít odvozené vztahy.15