EPIDEMIERS DYNAMIK

EPIDEMIERS DYNAMIK
AF
Kasper Larsen, Bjarke Vilster Hansen
Henriette Elgaard Nissen, Louise Legaard og
Charlotte Pletscher-Frankild
1. Miniprojekt
Sidefagssupplering, RUC
December 2007

INDLEDNING
Matematisk modellering kan anvendes til at forsimple virkeligheden, derefter regne på den
forsimplede virkelighed, og til sidst ud fra disse beregninger konkludere noget om virkeligheden på
den forsimplede matematiske baggrund. Det betyder, at der skal foretages en del begrænsninger og
antagelser, når virkeligheden omsættes til den matematiske model.
I denne opgave anvendes matematisk modellering til at kunne forudsige noget om epidemier og
deres udvikling og betingelserne for, at en epidemi i det hele taget vil opstå. Epidemier er
karakteriseret ved, at de starter med at vokse eksponentielt med større eller mindre hastighed, hvor
antallet af smitteramte vokser med en fordoblingstid. Efter en tid når epidemien et maksimum,
hvorefter epidemien dør ud igen.
Det er et meget vigtigt at vide noget om epidemier, da det er et område, der har krævet og kræver
mange menneskeliv på verdens plan. Man kan bare tænke på et historisk eksempel som ”Den Sorte
Død” i det 14. århundrede. Et nutidigt og meget bekymrende eksempel kan være AIDS-epidemien,
som hærger i store dele af specielt Afrika og Asien. Det er dermed tydeligt, at epidemier kan have
vidtrækkende samfundsmæssig betydning, og på den baggrund er det af vital betydning at kunne
forudsige noget om epidemiers opståen og udvikling, og det kan en matematisk modellering af
systemet give os et bud på.
PROBLEMFORMULERING
I dette projekt ses der på en matematisk model for udviklingen af epidemier udviklet af Kermack-
Mckendrick i 1927, den såkaldte SIR-model.
Der ses på spørgsmålene:
• Hvordan kan en model for udviklingen af en epidemi se ud?
• Hvilke parametre styrer dynamikken i en epidemi?
Formålet med dette projekt er at gennemgå en matematisk model for en generel epidemi og dens
udvikling og derefter at analysere modellen ved flere eksempler. Til sidst foretages der en udvikling
til en lidt anden type model.
2

Den overordnede gennemgang af modellen opdeles i følgende punkter
- SIR-modellen og dens parametre gennemgås
- Modellens differentialligninger gennemarbejdes
- Modellens begrænsninger gennemgås
- Modellens antagelser belyses
- Modellen analyseres ved hjælp af eksempler og fortolkning af disse
SIR-MODELLEN
SIR-modellen er en simpel, klassisk model, der har udbredelsen af epidemier som overordnet
genstandsområde. Vi vil karakterisere SIR-modellen som en forklarende/deterministisk epidemisk
model, der behandler epidemier af typen, hvor smitten overføres i et møde mellem et smittende og
et modtageligt individ, og hvor der efter en periode udvikles resistens. Gennem anvendelse af
sandsynlighedsteori har man opstillet en model, som beskriver deterministiske sammenhænge og
altså ”i princippet afgiver deterministiske kausalitetsudsagn og deterministiske prædiktioner”
Det samlede antal individer inddeles i tre grupper (kompartments) til brug for den videre model:
S: Individer, der er modtagelige for sygdommen (Susceptibles)
I: Individer, der er smittede og smittende (Infected)
R: Individer, der er immune (eller døde) (Removals)
Det samlede antal individer, N, som indgår i undersøgelsen (dvs. en hel befolkning eller blot en
risikogruppe, som udgør en afgrænset del af befolkningen), udgøres af de tre grupper, hvilket giver
følgende:
N= S+I+R
Modellen bygger på, at der sker en bevægelse af individer fra S-gruppen henover I-gruppen til R-
gruppen. Dette forklares med, at der i kontakten mellem en inficeret (I) og en modtagelig (S) kan
ske overførsel af smitte, hvorved et individ overgår fra S-gruppen til I-gruppen. Tilsvarende vil der
fra I-gruppen ske en bevægelse af individer til R gruppen pga. udvikling af immunitet eller død.
Modellen kan beskrives som en kompartmentmodel med følgende udsende:
3

Vi skal nu på en eller anden måde modellere bevægelsen fra S til I og fra I til R. Bevægelsen fra S
til I afhænger af både S og I, idet det virker logisk, at antallet af nyligt inficerede bestemmes af,
hvor mange der kan smittes, og hvor mange der er smittet (i hvert fald hvis smitten sker fra person
til person). Et møde, som foregår mellem en smittet person og en modtagelig person, og som fører
til, at den modtagelige person bliver smittet, kalder vi et effektivt møde. Antallet af effektive møder
en person fortager pr. tidsenhed kalder vi kontaktraten c. Kontaktraten afhænger derfor af mange
adfærdsmæssige og biologiske faktorer. I denne rapport tager definitionen af c sit udgangspunkt i, at
alle medlemmer af befolkningsgruppen har lige chancer for at møde alle andre medlemmer af
befolkningsgruppen. En modtagelig person foretager i tidsrummet Δt·c kontakter. Hvis N er det
samlede befolkningstal, vil brøkdelen I / N være kontakter med smittede personer. I / N betegner
sandsynligheden for på et givent tidspunkt, at en tilfældig person er smittende. Da der er S personer,
som kan udføre en given kontakt, er sammenhænget mellem flowet af personer fra I til S:
c
N
⋅ I ⋅ S ⋅ Δt
c
hvor betegner infektionsraten. Infektionsraten er et udtryk for, hvor smitsom en sygdom er. Des
N
c c ⋅ ∆t
mere smitsom en sygdom er, jo større bliver . Det vil sige, at
N
N
4
udtrykker sandsynligheden
for, at et inficerende individ inficerer et modtageligt individ inden for et givent tidsrum Δt.
I stedet for infektionsraten kan man i stedet, formulere sig ved brug af infektionsstyrken også kaldet
c
smitteraten. Smitteraten er givet ved udtrykket Λ = ⋅ I
N
er den rate, hvormed modtagelige individer bliver smittet, og er altså den komponent, der styrer
flowet fra S til I.
S I R
Bevægelsen fra I til R, altså hvor mange af de smittede der bliver resistente eller dør, afhænger kun
af, hvor mange der er syge, og ikke hvor mange der allerede er resistente (eller døde). Bevægelsen
fra I til R kan beskrives som, at en bestemt andel (procentdel) af de smittede bliver raske i løbet af

en tidsenhed. Andelen af smittede der bliver raske i løbet af en tidsenhed, kaldes removalrate og
betegnes med symbolet ν. Dermed kan vi beskrive overgangsstrømmen fra I til R som værende lig
I·ν.
Den samlede SIR model kommer skematisk til at se således ud:
og modellens ligninger, der beskriver S, I og R til det efterfølgende tidsskridt som værende
funktioner af det nuværende tidsskridt og ændringen i de givne grupper i løbet af tidsskridtet ∆t:
S(
t + Δt)
I ( t + Δt)
R(
t + Δt)
Med lidt omskrivninger er differensligningerne:
=
=
=
S(
t + Δt)
− S(
t)
Δt
I(
t + Δt)
− I(
t)
Δt
R(
t + Δt)
− R(
t)
Δt
c ⋅ S(
t)
⋅ I ( t)
S(
t)
−
⋅ Δt
N
c ⋅ S(
t)
⋅ I ( t)
I ( t)
+
⋅ Δt
− I(
t)
⋅ν
⋅ Δt
N
R(
t)
+ I(
t)
⋅ν
⋅ Δt
=
=
=
5
c ⋅ S(
t)
⋅ I(
t)
−
N
c ⋅ S(
t)
⋅ I(
t)
− I(
t)
⋅ν
N
I(
t)
⋅ν
Lader vi nu tidsskridtet gå mod nul, altså Δt → 0 , får vi differentialkvotienterne til S, I og R og
dermed følgende diffentialligningssystem:
S´(
t)
I´(
t)
R'(
t)
=
=
=
c ⋅ S(
t)
⋅ I(
t)
−
N
c ⋅ S(
t)
⋅ I(
t)
− I(
t)
⋅ν
N
I ( t)
⋅ν
Vi har kun brug for to af dem, idet vi ved at summen af de tre grupper altid er N, altså N = S(t) + I(t)
+ R(t) og dermed at S´(t) + I´(t) + R´(t) = N´ = 0.
c
⋅ I ⋅ S
ν
⋅ I
N
S I R

MODELLENS ANTAGELSER
Før vi ser nærmere på selve modellen, vil vi se lidt på de antagelser, der er gjort i forbindelse med
SIR-modellen. Opbygningen af SIR-modellen giver ikke mulighed for igen at miste sin resistens
(hvilket sker for nogle sygdomme, der f.eks. skyldes bakterieinfektioner), man kan altså ikke vende
tilbage til S-gruppen.
De resterende antagelser omhandler typisk bevægelser mellem grupperne S, I og R, som ikke alle
har været eksplicit formulerede. I forbindelse med nogle af antagelserne, vil der desuden blive givet
eksempler på hvor disse antagelser er eller kan være problematiske.
A. Grupperne er homogent blandede.
Det er klart, at sandsynligheden for kontakt mellem to individer fra forskellige grupper afhænger af
fordelingen af gruppernes individer. Hvis koncentrationen af S-individer er stor, vil et enkelt I-
individ have større ”chance” for at møde et S-individ, end hvis koncentrationen er lille. Er
grupperne derimod homogent fordelt, og individerne møder hinanden tilfældigt (og altså har lige
stor chance for at mødes), da vil infektionsraten være ensartet. Er der tale om sygdomme, der oftest
rammer bestemte befolkningsgrupper, kan denne antagelse være problematisk Et eksempel kunne
være, at visse kønssygdomme er overrepræsenteret blandt bøsser.
B. Infektionsrate og removalrate er konstante med hensyn til tiden.
Afhængigt af sygdomstypen kan smittefarligheden ændres med tiden. Hvis sygdommen f.eks. som
udgangspunkt er forårsaget af en bakterie, kan bakterien med tiden blive mere aggressiv som følge
af tilpasning til de nye livsbetingelser (et eksempel er malariamyggens udvikling af resistens mod
bestemte insekticider). Dette vil betyde, at den relative removalraten øges, og begyndelsesværdien
for antal modtagelige, S(0), tilsvarende falder. Det er naturligvis af altafgørende betydning, at man
kender til muligheden for ændringer i disse kritiske parametre.
C. De smittede individer bliver straks smittende.
I virkeligheden er der en latenstid, hvor de smittede individer går over til også at blive smittende, og
afhængig af denne latenstid størrelse, kan antagelsen resultere i en overvurdering af, hvor
fremskredet sygdommen vil være til et givet tidspunkt. Det vil dog kun have begrænset betydning,
6

idet der så vil gå tilsvarende længere tid, før et I-individ flyttes til R-gruppen og ikke længere udgør
en risiko. Dermed vil effekten i ”S-enden” udlignes af effekten i ”R-enden”.
D. Sygdommen smitter direkte fra person til person.
Denne antagelse kan diskuteres, idet modellen ikke definerer elementerne i S, I og R-grupperne. I
princippet kunne der således være smittefarlige dyr blandet ind i grupperne af mennesker, men i
realiteten vil det være umuligt med tilstrækkelig stor nøjagtighed at sætte give et skøn på antallet af
individer i de enkelte grupper. Antagelsen betyder, at modellen ikke tager højde for smitte, der
spredes fra dyr til mennesker, hvilket ofte vil være tilfældet (f.eks. Fugleinfluenza, hvor smittevejen
oprindeligt kun var gennem fugle, senere andre dyr, der er herunder nu også sjældne eksempler på
smitte gennem mennesker).
E. Alle personer er lige modtagelige for sygdommen.
Risikoen for smitte afhænger naturligvis bl.a. af immunforsvaret og af den menneskelige adfærd.
Man kan derfor ikke regne med en fast infektionsrate helt uafhængigt af det enkelte møde mellem et
smittende og et modtagende individ. Man kan dog bruge en gennemsnitlig infektionsrate for
beregningerne af sygdomsudviklingen i den samlede befolkning, og det er i realiteten også sådan
modellen anvendes.
F. Antallet af modtagelige er konstant.
Ser vi på epidemiologiske undersøgelser og beregninger, der strækker sig over generationer, kan
antallet af individer i risikogruppen ændre sig, hvilket vil have betydning for det endelige billede af
sygdomsudviklingen. F.eks. er fødselsraten faldet markant bl.a. i de vestlige lande og i Japan, men
dette modsvares delvist af en forøget levetid. Befolkningen vil i lande, hvor det samlede antal
individer reduceres (og det er jo faktisk det, vi ser mange steder i Europa) være mindre sårbar for
smitte end modellen antager. Dette faktum skal man naturligvis tage højde for, når man laver
fremtidsprognoser.
7

MODELLENS OPFØRSEL
Hvordan ændrer de forskellige gruppers størrelse sig med tiden, og hvilken betydning har de
forskellige indgående parametre (c, ν) og begyndelsesbetingelserne S(0), I(0), R(0). For at få en ide
hertil vil vi se på en række eksempler.
Vi vil betragte en række tilfælde, hvor vi ved at ændre på nogle af parametrene vil se, om og i så
fald hvordan epidemier – ifølge modellen – vil udvikle sig. I de første seks eksempler, vil vi lade
c c
infektionsraten og removalraten v være konstante, og vi sætter = 0,0003 og v = 0,55. Vi vil i
N
N
alle eksemplerne lade R(0) = 0, altså at der ikke er nogle resistente til at begynde med. I det første
eksempel vil vi lade S(0) = 3500, I(0) = 50. Dette første eksempel vil vi betragte som vores
”standardeksempel”, dvs. i forhold til hvilket vi vil sammenligne ved justeringen af de to parametre
S(0) og I(0).
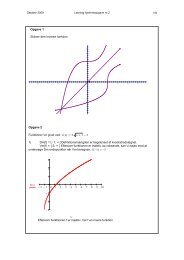
SIR modellen, eksempel 1
På Figur 1 kan forløbet af S(t), I(t) og R(t) følges, når S(0) = 3500 og I(0) = 50. Hvis vi skal se på
det som et ”virkeligt” eksempel, er der til starttidspunktet tale om en population bestående af 3550
individer, hvoraf de 50 er inficerede. Det ses, at antallet af inficerede individer hurtigt stiger fra de
50 til et antal på ca. 500 ved t = 7,5. Derefter falder antallet af individer, der er modtagelige overfor
sygdommen kraftigt, idet antallet af individer, der er resistente eller døde, er steget. Antallet af
inficerede individer falder herefter igen og går mod nul, hvilket betyder, at epidemien udryddes.
Hvis vi udelukkende betragter R(t) som antallet af døde individer, vil altså en stor del af
befolkningen blive udryddet (ca. 2825 individer), mens antallet af modtagelige S(t) vil være
aftagende og stabilisere sig på ca. 725 individer.
8

Figur 1: Illustration af eksempel 1. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 3500, I(0) = 50, R(0) = 0, N = 3550, c/N = 0,0003 og ν = 0,55.
SIR modellen, eksempel 2
I dette eksempel lader vi populationen være 3600 individer, hvoraf 100 er smittede/smittende og
ingen er resistente. Dvs. vi har N = 3600, I(0) = 100, R(0) = 0, og altså S(0) = 3500. Infektionsraten,
c/N, er stadig 0,0003, mens removalraten, ν, er fastholdt på 0,55. Parametrene S(t), I(t) og R(t) vil
nu udvikle sig som vist på Figur 2.
9

Figur 2: Illustration af eksempel 2. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 3500, I(0) = 100, R(0) = 0, N = 3600, c/N = 0,0003 og ν = 0,55.
På figuren ser vi at S(t) er aftagende gennem hele intervallet og stabiliserer sig ved ca. 750
individer, mens R(t) er stigende i hele intervallet og stabiliserer sig ved ca. 2850 individer.
Udviklingen af inficerede (I(t)) stiger fra t = 0 til t ≈ 6,5, så modellen viser, at der er en epidemi.
Efter t ≈ 6,5 hvor antallet af inficerede individer var nået op på knapt 600, er I(t) aftagende i resten
af intervallet og nærmer sig langsomt 0.
10

SIR modellen, eksempel 3
Vi lader nu antallet af modtagelige individer til tiden 0 være det dobbelte af antallet i det første
eksempel, dvs. S(0) = 7000. I(0) sættes igen til 50. Nu er altså en betydelig mindre andel af
befolkningen inficerede til tiden 0. Forløbet af grafen viser imidlertid et noget mere drastisk forløb
end i de to foregående eksempler. Udviklingen af inficerede stiger endnu hurtigere end før og når et
maksimum på ca. 2750, hvorefter den falder igen. Antallet af resistente stiger tilsvarende kraftigt,
og vil med tiden udgøre langt hovedparten af den samlede befolkning, og tilsvarende af
modtagelige S(t) falde og stabilisere sig på ca. 200 individer. Der er altså i dette tilfælde tale om
nærmest en total populationsudryddelse (hvis vi altså betragter R(t) som antallet af døde). Når S(0)
er meget stor i forhold til den relative removalrate, og I(0) udgør en mindre del af den samlede
population fås altså en ret drastisk udvikling af epidemien.
Figur 3: Illustration af eksempel 3. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 7000, I(0) = 50, R(0) = 0, N = 7050, c/N = 0,0003 og ν = 0,55.
SIR modellen, eksempel 4
Lad igen S(0) = 7000 men lad I(0) = 100. De resterende parametre er som i eksempel 1. Figuren
vises nogenlunde det samme som eksempel 3. Det ses altså igen, at det ikke har store betydning, om
en lidt større del af befolkningen er smittet fra starten.
11

Figur 4: Illustration af eksempel 4. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 7000, I(0) = 100, R(0) = 0, N = 7100, c/N = 0,0003 og ν = 0,55.
SIR modellen, eksempel 5
I forhold til det første eksempel, vil vi nu halvere antallet af modtagelige individer, så S(0) = 1750.
I(0) = 50. Det ses at I(t) er svagt aftagende i hele forløbet, så der er altså ikke tale om en epidemi.
R(t) er stigende, mens S(t) er aftagende, men i dette tilfælde krydser de ikke hinanden. Det vil sige
at antallet af modtagelige forbliver betydeligt større (ca.1450 individer) end antallet af resistente
eller døde (ca.350 individer).
12

Figur 5: Illustration af eksempel 5. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 1750, I(0) = 50, R(0) = 0, N = 1800, c/N = 0,0003 og ν = 0,55.
SIR modellen, eksempel 6
Vi betragter nu tilfældet S(0) = 1750, I(0) = 100, R(0) = 0 og altså N = 1850. Removalraten, ν,
sættes vi til 0,55, mens vi har bestemt os for en infektionsraten, c/N, sættes til 0,0003. Altså er den
eneste forskel til eksempel 2 at S(0) er blevet halveret. Parametrene S(t), I(t) og R(t) vil nu udvikle
sig som vist på Figur 6.
13

Figur 6: Illustration af eksempel 6. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 1750, I(0) = 100, R(0) = 0, N = 1850, c/N = 0,0003 og ν = 0,55.
S(t) er som i eksempel 2 aftagende gennem hele intervallet, mens R(t) er stigende gennem hele
intervallet. Antallet af modtagelige individer S(t) stabiliserer sig med tiden ved ca. 1300, mens
antallet af resistente/døde med tiden stabiliserer sig ved ca. 550 individer.
I dette tilfælde ser vi, at antallet af smittede/smittende, I(t), falder gennem hele intervallet. Der er
altså i dette tilfælde ikke tale om en epidemi. I(t) går dog som i de tidligere eksempler mod 0 med
tiden.
c
I de sidste to eksempler vil vi se hvad der sker, når vi justerer på værdierne for infektionsraten
N
og removalraten v.
SIR modellen, eksempel 7
c
Lad som i det første eksempel S(0) = 3500 og I(0) = 50. Vi sætter nu infektionsraten til = 0 og
N
removalraten til v=1. Figuren viser nu – hvilket også gerne skulle være tilfældet – at antallet af
modtagelige ikke ændrer sig (forbliver på 3500 individer), og at de inficerede hurtigt bliver
14

esistente. Når infektionsraten er 0, kan der naturligvis ikke ske nogen bevægelse fra gruppen af
modtagelige over i gruppen af inficerede.
Figur 7: Illustration af eksempel 7. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 3500, I(0) = 50, R(0) = 0, N = 3550, c/N = 0 og ν = 1.
SIR modellen, eksempel 8
c
Vi sætter S(0) = 3500 og I(0) = 50. Infektionsraten sættes nu til = 1og
removalraten til v = 0. Da
N
v = 0 vil der selvfølgelig ikke ske nogen bevægelse fra gruppen af inficerede over i gruppen af
resistente. Grafen viser derfor også, at antallet af resistente forbliver konstant på 0. Samtidig ser vi,
at alle fra gruppen af modtagelige individer på meget kort tid blive inficeret. Dvs. S(t) falder hurtigt
og stabiliserer sig på 0, mens I(t) tilsvarende stiger og stabiliseres på 3550.
15

Figur 8: Illustration af eksempel 8. De tre gruppers (S(t), I(t) og R(t)) størrelse afbilledet som funktion af tiden.
S(0) = 3500, I(0) = 50, R(0) = 0, N = 3550, c/N = 1 og ν = 0.
I de ovennævnte eksempler, har vi forsøgt at illustrere, hvorledes parametrene S(t), I(t) og R(t)
påvirker hinanden. Vi bemærkede, at når c/N, ν, I(0) og R(0) blev holdt konstant, udviklede de tre
parametre S(t), I(t) og R(t) sig meget forskelligt afhængigt af størrelsen af S(0).
Som vi har kunnet se ud fra eksemplerne, tyder det på, at S(t) er en aftagende funktion, mens R(t) er
en voksende funktion.
Dette kan forklares ud fra differentialligningerne, hvorom der gælder, at når I(t), S(t), c/N og ν er
positive:
S'
( t)
R'(
t)
=
=
c
− ⋅ S(
t)
⋅ I(
t)
N
ν ⋅ I(
t)
16
⇒
⇒
S'
( t)
< 0
R'(
t)
> 0
Men at det forholder sig således, er dog ikke specielt underligt, idet modellen er konstrueret, så der
kun kan flyttes individer ud af S-gruppen, mens der kun kan flyttes individer ind i R-gruppen.
Hvilken værdi, de to funktioner konvergerer mod, er lidt sværere at bestemme. Vi (eller man) har
ikke kunnet løse differentialligningssystemet, men har kun kunnet finde sammenhængene:

ν
ν
S(
t)
+ I(
t)
− ln( S(
t))
= S(
0)
+ I ( 0)
− ln( S(
0))
c N
c N
⎛ c N
⎞
S(
t)
= S(
0)
⋅ exp⎜−
( R(
t)
− R(
0))
⎟ > 0
⎝ ν
⎠
Opskrivningen af I(t) er, som vi kan se af ovenstående eksempler, noget kompliceret, men man kan
med sikkerhed sige, at I(t) med tiden vil gå med nul, idet alle inficerede vil blive resistente med
tiden (forudsat at ν > 0).
I vores ovenstående eksempler er der tale om en epidemi, hvis S(0) = 3500 eller 7000, men ikke
hvis S(0) = 1750. I tilfældene, hvor der ikke er tale om epidemier, er I(t) en aftagende funktion i
hele intervallet, mens I(t) har et maksimum hvis der er tale om en epidemi. Vi er heldigvis i stand til
at afgøre om givne betingelser vil føre til en epidemi, hvilket vi vil se på i det følgende.
Betingelser for opståen af en epidemi
En væsentlig begrundelse for at udvikle modeller er netop at skabe viden, der i sin optimale
anvendelse hindrer udviklingen af en epidemi. At vi således kan handle i tide, hvis vi ser, at
betingelserne for udviklingen af en epidemi er til stede. Modellen skal, om man så må sige, bibringe
os en indsigtsfuld handleparathed.
Hvis vi skal udtale os om de i virkeligheden ret komplicerede processer, som er involveret i
sygdomsspredning, må vi i første omgang se nærmere på differentialligningerne:
⎛ S(
t)
⋅ c ⎞
Det følger af ligningen for tilvæksten i individantallet i gruppen I, at I ( t)
⋅ ⎜ −ν
⎟ > 0 hvis
⎝ N ⎠
⎛ S(
t)
⋅ c ⎞
⋅ N
sygdommen er i udvikling. Det vil sige ⎜ −ν
⎟ > 0 og altså S t >
⎝ N ⎠
c
ν ν ⋅ N
( ) , hvor
c
udtryk for den relative removalrate, som er forholdet mellem removalrate og infektionsraten. Disse
resultater giver os nemt den vigtige tærskelsætning:
Tærskelsætningen: Der opstår en epidemi, hvis begyndelsesværdien for antal modtagelige, S(0),
overstiger den relative removalrate.
S
0
ν
⋅ N
>
c
⇔
17
S0
⋅ c
T = > 1
ν ⋅ N
er et

hvor T er den såkaldte reproduktionsrate.
Denne vigtige parameter udtrykker, hvor mange individer, den inficerende når at smitte, inden
vedkommende selv bliver resistent og således ikke længere er smittefarlig, under antagelse af at alle
i befolkningen er modtagelige.
Hvis man kender sygdommens infektionsrate og removalrate, giver modellen altså et direkte
anvendeligt udtryk for, om en given befolknings gruppe vil udvikle en epidemi, med mindre der
sættes relevante tiltag i værk. (Med relevante tiltag menes handlinger, der har til hensigt at
begrænse smittespredning, dvs. isolation af inficerende individer, sygdomsbehandling, styrkelse af
immunforsvaret hos risikogrupper o. lign).
Af udtrykket ses det også, at jo større en befolkning er, desto mere sårbar er den for epidemier. Det
kan forklares med, at smittespredningen er større i en stor befolkning end i en lille, fordi
sandsynligheden for kontakt mellem et inficerende og et modtageligt individ øges med
befolkningstallet.
Det giver altså mening, at isolere grupper af befolkningen og dermed undgå eller begrænse
kontakten mellem individerne. Dette kan naturligvis være yderst problematisk i områder af verden,
hvor de sociale og sanitære forhold er katastrofale, og hvor mennesker og dyr lever mellem
hinanden uden tag over hovedet.
Udtrykket viser desuden, at hvis man reducerer infektionsraten og/eller øger removalrate (der i
modellen antages at være konstante), så mindskes risikoen for at en given befolkning overskrider
tærsklen for epidemiens udvikling.
Tærskelværdien er et begreb, der både indeholder information om sygdommens spredningsevne,
men også om befolkningens sygdomshistorie. En forenkling af tærskelsætningen, hvor man antager
at hele befolkningen er modtagelige ved epidemiens start, altså at S(0) = N, R(0) = 0 og I(0) 1.
Det er et udtryk, der kun indeholder oplysninger om
ν
kontaktraten og removalraten.
Epidemiens forløb
Som sagt, er I(t) en noget kompliceret funktion, der opfører sig forskelligt under forskellige
betingelser, dog altid til slut gående mod 0. Dette afsnit prøver vi yderligere at beskrive I(t). Nogle
gange er I(t) en aftagende funktion i hele tidsintervallet, men det er hvis der ikke opstår en epidemi,
18

altså hvis S(0) er mindre end tærskelfrekvensen. Det betyder at I(t) er en aftagende funktion hvis
Hvis derimod
ν
S(
0)
< .
c N
ν
S(
0)
> , altså S(0) er større end tærskelfrekvensen vil der opstå en epidemi. I(t)
c N
vil i dette tilfælde stige til en maksimumværdi, hvorefter den vil være aftagende. Denne
maksimumværdi for I(t) vil indtræde til det tidspunkt t, hvor
en epidemi ikke længere er til stede.
19
ν
S(
t)
= , dvs. når betingelserne for
c N
Formen på I(t), specielt nær endepunkterne, kan i tilfælde af en epidemi yderligere beskrives på
følgende måde. Vi må forvente, at S(t) er en konstant for t < 0. Da vi også ved, at c/N og ν er
konstante, kan vi altså i ligningen
⎛ S(
t)
⋅ c ⎞
I´(
t)
= I(
t)
⋅⎜
−ν
⎟
⎝ N ⎠
⎛ S ( t)
⋅ c ⎞
betragte ⎜ −ν
⎟ som en konstant k1. Dermed har vi altså, at I ′ ( t)
= k1
⋅ I(
t)
. Denne simple
⎝ N ⎠
differentialligning har som bekendt løsningen
eksponentielt i starten af en epidemi.
I ( t)
⋅
Omvendt vil det i slutningen af en epidemi gælde, at
k1t
= c1
e . Det vil sige, at I(t) vil stige
ν
S(
t)
< og S(t) går mod en konstant. I
c N
⎛ S(
t)
⋅ c ⎞
dette tilfælde vil vi få en ny konstant: k2
= ⎜ −ν
⎟ . Denne konstant vil være negativ, idet
⎝ N ⎠
c ν
k 2 < ⋅ −ν
= 0 og vi vil derfor få en eksponentielt aftagende funktion I ( t)
⋅
N c N
k2t
= c2
e . Dette vil
altså betyde, at antallet af inficerede og inficerende individer vil aftage eksponentielt i slutningen af
en epidemi.
Vaccination
De antagelser, der blev gjort under gennemgangen af SIR-modellen gælder stadig her. Vi vil
undersøge, hvordan epidemimodellen ser ud, når vi antager, at en vis procentdel af individerne er

vaccineret mod sygdommen, som det er tilfældet for børnesygdomme som for eksempel mæslinger,
fåresyge og røde hunde (MFR-vaccinen).
Vi antager at en brøkdel, p, af individerne vaccineres før sygdommen bryder ud. SIR-modellen kan
anvendes med de samme antagelser som i det foregående, men med nye begyndelsesbetingelser.
Således er begyndelsesværdien af antal modtagelige individer S(t0) = (1-p)S0. Antal inficerede og
inficerende individer er ved sygdommens start stadig I(t0) = I0. Antallet af immune individer er R(t0)
= R0 + pS0 ved starten af den mulige epidemi. Bemærk at det totale antal individer stadig er N, idet
S(t0) + I(t0) + R(t0) = (1-p)S0 + I0 + R0 + pS0 = N.
Tærskelværdien, der som nævnt, udtrykker hvor mange individer, der smittes af den inficerende,
inden vedkommende bliver resistent, er med de nye begyndelsesværdier givet ved:
c ⋅ ( 1−
p)
⋅ S0
T =
.
ν ⋅ N
Denne værdi er dermed reduceret med en faktor ( 1−
p)
i forhold til tærskelværdien for SIR-
modellen uden vaccination. Da de inficerede individer, dermed smitter færre individer, før de bliver
resistente, er vaccination, som forventet, et godt tiltag mod udviklingen af en epidemi.
Med hensyn til den omstridte MFR-vaccine, er vurderingen fra Statens Serum Institut da også, at
vaccinen har virket positivt på folkesundheden. Siden 2003 er der ikke konstateret nogen tilfælde af
mæslinger, og siden samme år er der heller ikke registreret nogen tilfælde af røde hunde blandt
gravide og nyfødte.
KONKLUSION
I opgaven har vi betragtet SIR-modellen og opstillet en række eksempler til at illustrere
sammenhængen mellem de indgående parametre. Der er gjort en række antagelser for at kunne opnå
en relativt simpel matematisk model til beskrivelse af en epidemis udvikling. En række af disse
antagelser vil naturligvis ikke være opfyldt i de fleste virkeligt forekommende populationer, og
modellen er dermed at betragte som en forsimpling af virkeligheden. Det at opstille modeller for
fænomener, hvor komplicerede forhold som f.eks. menneskers adfærd spiller ind, må vi betragte
som yderst vanskeligt. En adækvat matematisk beskrivelse af epidemiers udvikling vil nok aldrig
20

helt kunne lade sig gøre. Ikke desto mindre mener vi, at modellen giver en udmærket forståelse af
hvilke faktorer, der spiller ind i forhold til udviklingen af en epidemi.
Vi har altså fundet, at S(t) er en aftagende funktion, der med tiden stabiliseres, og med tiden går
mod en konstant værdi k.
R(t) er omvendt en tiltagende funktion, der med tiden stabiliseres og med tiden går mod en anden
funktion givet ved N-k.
I(t), der beskriver forløbet af smittende/smittede, vil med tiden gå mod 0. Hvis S(0) er mindre end
eller lig den relative removalrate, vil I(t) være aftagende i hele intervallet, og der opstår ingen
epidemi. Hvis omvendt S(0) er større end den relative removalrate, vil I(t) først vokse, indtil S(t) er
lig den relative removalrate, hvorefter den igen vil være aftagende. I det sidste tilfælde er der altså
tale om en epidemi. I(t) vil i dette tilfælde i begyndelsen vokse ekspotentielt og til sidst aftage
ekspotentielt.
21