Apsel Stetigkeit und Differenzierbarkeit Dezember ... - Matthias Apsel

Apsel Stetigkeit und Differenzierbarkeit Dezember 2001
Stetigkeit: Eine Funktion ist stetig in x0, wenn gilt f ( x)
= f ( x ) .
Seite 1
lim 0
→x
x 0
Sie ist stetig in einem Intervall, wenn sie in jeder Stelle stetig ist.
Anschaulich: Wenn die x-Werte „zusammenrutschen“, dann
„rutschen“ auch die y-Werte „zusammen“.
Die Funktion hat keinen Sprung.
f ( x)
− f ( x 0 )
Differenzierbarkeit: Eine Funktion ist diff´bar in x0 wenn lim existiert.
x→x 0 x − x 0
Sie ist diff´bar in einem Intervall, wenn sie in jeder Stelle diff´bar ist.
Anschaulich: Die Funktion hat keinen Sprung und keinen Knick.
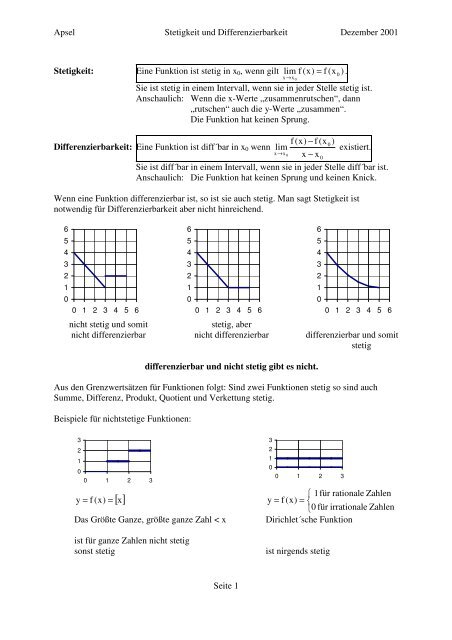
Wenn eine Funktion differenzierbar ist, so ist sie auch stetig. Man sagt Stetigkeit ist
notwendig für Differenzierbarkeit aber nicht hinreichend.
6
5
4
3
2
1
0
0 1 2 3 4 5 6
nicht stetig und somit stetig, aber
nicht differenzierbar nicht differenzierbar differenzierbar und somit
stetig
differenzierbar und nicht stetig gibt es nicht.
Aus den Grenzwertsätzen für Funktionen folgt: Sind zwei Funktionen stetig so sind auch
Summe, Differenz, Produkt, Quotient und Verkettung stetig.
Beispiele für nichtstetige Funktionen:
3
2
1
0
0 1 2 3
6
5
4
3
2
1
0
0 1 2 3 4 5 6
y = f ( x)
= [ x]
⎧ 1für
rationale Zahlen
y = f ( x)
= ⎨
⎩0
für irrationale
Zahlen
Das Größte Ganze, größte ganze Zahl < x Dirichlet´sche Funktion
ist für ganze Zahlen nicht stetig
sonst stetig ist nirgends stetig
3
2
1
6
5
4
3
2
1
0
0
0 1 2 3
0 1 2 3 4 5 6

Apsel Stetigkeit und Differenzierbarkeit Dezember 2001
Aufgabe:
Gegeben sind die Funktionenscharen
Drei Vertreter sind dargestellt
10
8
6
4
2
0
-4 -3 -2 -1 0 1 2 3 4
y = f
m ; n
(
x)
0
-4 -3 -2 -1 0 1 2 3 4
Seite 2
2 ⎧x
= ⎨
⎩mx
+ n
für x ≤ 2
.
für x > 2
Im Allgemeinen sind diese Funktionen in x0=2 nicht stetig. (Bild 1)
Welche Bedingung muss an m und n gestellt werden, damit die Funktion in x0=2 stetig wird?
Für welches m und n ist die Funktion in x0=2 differenzierbar?
10
8
6
4
2
10
8
6
4
2
0
-4 -3 -2 -1 0 1 2 3 4