Höhere Mathematik

89. Ableitungsbegriff und Ableitungsregeln 457
(e) Die Ableitung von f(x) =e x erhält man, indem
man f als Umkehrfunktion von g(x) :=lnx auffaßt und
dann die Umkehrregel anwendet; es ergibt sich f ′ (x) =
(g −1 ) ′ (x) =1/g ′� f(x) � =1/ � 1/f(x) � = f(x) =e x .Die
Funktion f ist also – wie bereits in (89.10) durch direkte
Rechnung hergeleitet – ihre eigene Ableitung.
(f) Die Ableitung der für x>0 definierten Funktion
f(x) =x x = e x ln x ist nach Teil (e) und der Ketten- und
der Produktregel gegeben durch f ′ (x) =e x ln x · (ln x +
x/x) =x x (1 + ln x). �
Es folgt ein Beispiel dafür, daß die Ableitungsfunktion
einer differentiierbaren Funktion nicht zwangsläufig
stetig sein muß.
(89.15) Beispiel. Wir betrachten die Funktion
f(x) :=
� x 2 sin(1/x), falls x �= 0;
0, falls x =0.
Man überzeugt sich leicht davon, daß f auf ganz R differentiierbar
ist mit
f ′ (x) =
� 2x sin(1/x) − cos(1/x), falls x �= 0;
0, falls x =0.
Wir sehen, daß f ′ an der Stelle 0 zwar definiert, aber nicht
stetig ist. (Die folgenden Abbildungen zeigen die Graphen
von f und f ′ mit einer Skalierung um den Faktor 10.)
0.2
0.15
0.1
0.05
-0.2 -0.15 -0.1 -0.05 0.05 0.1 0.15 0.2
-0.05
-0.1
-0.15
-0.2
Abb. 89.4: Graph der Funktion f(x) =10x 2 sin(1/x).
-0.2 -0.15 -0.1 -0.05 0.05 0.1 0.15 0.2
Verlag Harri Deutsch – Karlheinz Spindler: Höhere Mathematik – Ein Begleiter durch das Studium – (978-3-8171-1872-4)
10
5
-5
-10
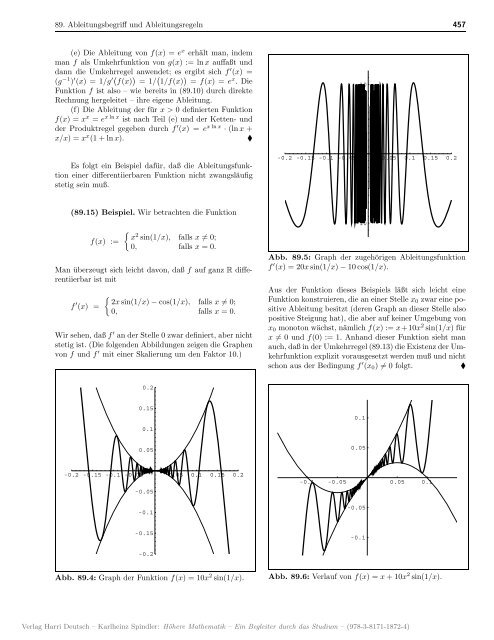
Abb. 89.5: Graph der zugehörigen Ableitungsfunktion
f ′ (x) =20x sin(1/x) − 10 cos(1/x).
Aus der Funktion dieses Beispiels läßt sich leicht eine
Funktion konstruieren, die an einer Stelle x0 zwar eine positive
Ableitung besitzt (deren Graph an dieser Stelle also
positive Steigung hat), die aber auf keiner Umgebung von
x0 monoton wächst, nämlich f(x) :=x+10x 2 sin(1/x) für
x �= 0 und f(0) := 1. Anhand dieser Funktion sieht man
auch, daß in der Umkehrregel (89.13) die Existenz der Umkehrfunktion
explizit vorausgesetzt werden muß und nicht
schon aus der Bedingung f ′ (x0) �= 0folgt. �
0.1
0.05
-0.1 -0.05 0.05 0.1
-0.05
-0.1
Abb. 89.6: Verlauf von f(x) =x +10x 2 sin(1/x).