Höhere Mathematik

540 Differentialrechnung auf Mannigfaltigkeiten
Da sich jede Mannigfaltigkeit lokal parametrisieren
läßt, können wir zumindest im Prinzip jede Optimierungsaufgabe
auf einer Mannigfaltigkeit M so lösen wie die Aufgaben
in den beiden vorangegangenen Beispielen. (Existiert
keine globale Parametrisierung von M, somüssen
wir mehrere verschiedene lokale Parametrisierungen betrachten,
und zwar so, daß die zugehörigen Kartenbereiche
ganz M überdecken; das ist aber kein prinzipielles
Problem.) Ist allerdings eine Mannigfaltigkeit M durch
ein reguläres Gleichungssystem g1(x) =··· = gm(x) =0
gegeben, so ist es oft mühsam oder aufwendig, eine Parametrisierung
von M zu finden und dann mit dieser zu
arbeiten. Es stellt sich daher die Frage, ob man ein Optimierungsproblem
auf M nicht direkt unter Benutzung der
Funktionen gi lösen kann. Der folgende Satz zeigt, daß
dies tatsächlich möglich ist.
(98.3) Satz von Lagrange. Es seien M ⊆ R n eine
Mannigfaltigkeit und f : M → R eine C 1 -Funktion.
Nimmt f an der Stelle p ∈ M ein lokales Minimum oder
Maximum an und hat M in einer Umgebung von p eine
reguläre Darstellung g1(x) = ··· = gm(x) = 0, so
gibt es Zahlen λ1,...,λm ∈ R (sogenannte Lagrange-
Multiplikatoren) mit
(⋆) (∇f)(p) = λ1 · (∇g1)(p)+···+ λm · (∇gm)(p) .
Beweis. Für jede in M verlaufende Kurve t ↦→ α(t)
mit α(0) = p hat die Funktion t ↦→ f � α(t) � ein Minimum
bzw. Maximum an der Stelle t = 0; also gilt
0 = d
�
�
�
dt�
f
t=0
� α(t) � = 〈(∇f)(p), ˙α(0)〉 .
Da α beliebig war, liegt also (∇f)(p) in(TpM) ⊥ .Nach
(97.17) wird aber (TpM) ⊥ aufgespannt von den Vektoren
(∇gi)(p) mit1≤ i ≤ m.
(98.4) Bemerkung. Wir wollen für den Spezialfall
einer Funktion f : R 2 → R und einer einzelnen Nebenbedingung
g(x, y) = 0 eine geometrische Deutung der Lagrangeschen
Methode geben. Da aufgrund der vorausgesetzten
Regularität ∇g �= 0 gilt, beschreibt die Gleichung
g(x, y) = 0 eine Kurve in R 2 . Wenn diese in irgendeinem
Punkt p transversal zu der Höhenlinie von f durch
p verläuft (diese also kreuzt), kann f entlang dieser Kurve
kein Minimum oder Maximum annehmen; wir müssen
ja von p aus nur ein kleines Stückchen in der einen oder
andern Richtung der Kurve laufen, um Höhenlinien von
f zu kleineren bzw. größeren Werten zu erreichen. Nimmt
also umgekehrt f in p ein Maximum oder Minimum unter
der Nebenbedingung g =0an,soistdiesnurmöglich,
wenn die Höhenlinien von f and g an der Stelle p tangential
zueinander verlaufen. Das bedeutet aber, daß die
Gradienten von f und g an dieser Stelle linear abhängig
sind (also in die gleiche oder in die exakt gegengesetzte
Richtung zeigen).
Verlag Harri Deutsch – Karlheinz Spindler: Höhere Mathematik – Ein Begleiter durch das Studium – (978-3-8171-1872-4)
g=0
f=c4
f=c1
f=c2
f=c3
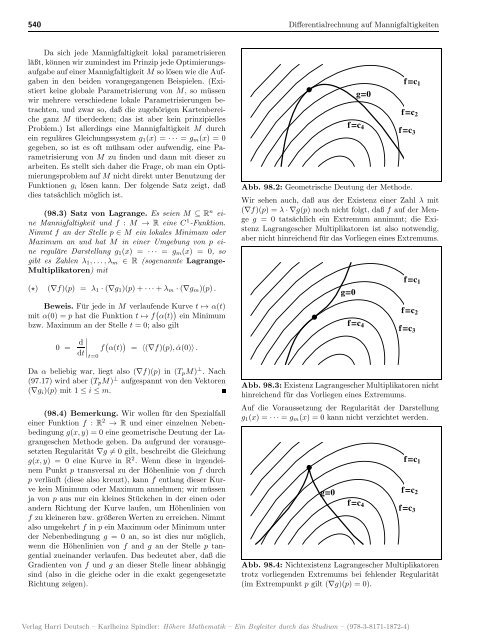
Abb. 98.2: Geometrische Deutung der Methode.
Wir sehen auch, daß aus der Existenz einer Zahl λ mit
(∇f)(p) =λ ·∇g(p) noch nicht folgt, daß f auf der Menge
g = 0 tatsächlich ein Extremum annimmt; die Existenz
Lagrangescher Multiplikatoren ist also notwendig,
aber nicht hinreichend für das Vorliegen eines Extremums.
g=0
f=c4
f=c1
f=c2
f=c3
Abb. 98.3: Existenz Lagrangescher Multiplikatoren nicht
hinreichend für das Vorliegen eines Extremums.
Auf die Voraussetzung der Regularität der Darstellung
g1(x) =···= gm(x) = 0 kann nicht verzichtet werden.
g=0
f=c4
f=c1
f=c2
f=c3
Abb. 98.4: Nichtexistenz Lagrangescher Multiplikatoren
trotz vorliegenden Extremums bei fehlender Regularität
(im Extrempunkt p gilt (∇g)(p) =0).