Reelle Funktionen.pdf
Reelle Funktionen.pdf
Reelle Funktionen.pdf
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
§9 <strong>Reelle</strong> <strong>Funktionen</strong><br />
(9.1) a) Eine reelle Funktion f besteht aus einer Menge Df und einer<br />
Vorschrift, die jedem x Df genau eine Zahl fx zuordnet.<br />
(Bezeichnung: f : Df : x fx )<br />
Df heißt der Definitionsbereich von f .<br />
( fx steht für die Zuordnungsvorschrift, nicht für die Funktion !!! )<br />
b) f Df : fx / x Df heißt die Wertemenge von f .<br />
c) Gf : x, fx / x Df 2 heißt der Graph von f .<br />
Beispiele:<br />
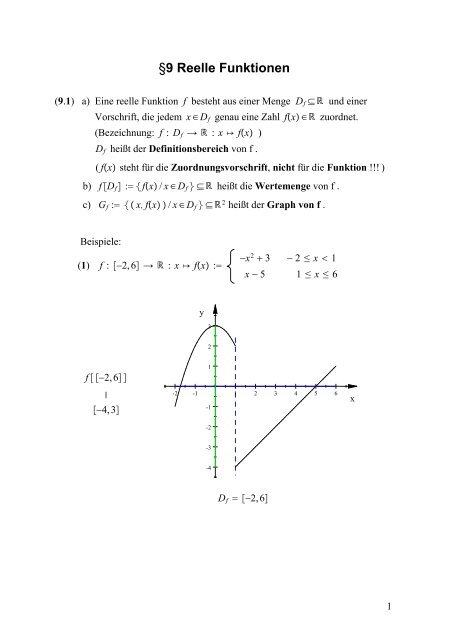
(1) f : 2, 6 : x fx :<br />
f 2, 6 <br />
<br />
4, 3<br />
y<br />
3<br />
2<br />
1<br />
x 2 3 2 x 1<br />
x 5 1 x 6<br />
-2 -1 1 2 3 4 5 6<br />
-1<br />
-2<br />
-3<br />
-4<br />
Df 2, 6<br />
x<br />
1
(2)<br />
(3)<br />
x fx<br />
2 5<br />
2<br />
3<br />
2<br />
2 3<br />
2<br />
3 3<br />
9<br />
2<br />
2<br />
5 3<br />
2<br />
2 3 -3 -2 -1 1 2 3 4 5 6 7<br />
Df 2, 2 , 2 , 3, 9<br />
3 2 , 5, 2 , f Df 3 , 3 , 2, 3, 5<br />
2<br />
1.0<br />
0.8<br />
0.6<br />
0.4<br />
0.2<br />
-0.2<br />
-0.4<br />
-0.6<br />
-0.8<br />
-1.0<br />
-1.2<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
-1<br />
-2<br />
2 4 6 8 10 12 14 16 18 20<br />
f : : n fn : 1n<br />
n<br />
Df , f Df 1, 1 , 1 , 1 , 1 , 1 , . . . . <br />
2 3 4 5 6<br />
2
(9.2) Seien f, g reelle <strong>Funktionen</strong> , .<br />
a) Ist Df Dg : D , so gewinnen wir neue <strong>Funktionen</strong> f, f g, fg,<br />
durch<br />
Df : D und fx : fx faches,<br />
Dfg : D und f gx : fx gx ( Summe ) ,<br />
Dfg : D und fgx : fxgx (Produkt) ,<br />
D f g<br />
: D \ x Df / gx 0 und f<br />
g x : fx<br />
=<br />
gx<br />
b) Ist gDg Df , so gewinnen wir eine neue Funktion f g<br />
(lies: „ f nach g ”) durch<br />
Dfg : Dg und f gx : f gx <br />
(Komposition, Verkettung, Hintereinanderausführung.)<br />
Beispiele: (1) fx sin x , gx x 2 x , Df Dg .<br />
f<br />
g x , D f g<br />
(2) fx sin 2 x , Df . gx x , Dg x / x 0.<br />
gDg Df ?, d.h.<br />
<br />
f<br />
g<br />
(Quotient) .<br />
f g existiert (?) mit f gx , Df g .<br />
f Df Dg ? , d.h.<br />
g f existiert ? .<br />
3
(9.3) Die reelle Funktion f heißt umkehrbar , falls eine Funktion f 1 existiert<br />
mit D f 1 f Df , f 1 D f 1 Df , f 1 fx x für alle x Df ,<br />
f f 1 x x für alle x D f 1.<br />
f 1 ist dann eindeutig bestimmt und heißt die Umkehrfunktion von f .<br />
(G f 1 ergibt sich durch Spiegelung von G f an der „Hauptdiagonalen”.<br />
Formal ergibt sich f 1 durch Auflösen der Gleichung fy x nach y.<br />
( fy x y f 1 fy f 1 x ))<br />
(9.4) f umkehrbar ( Für alle x1, x2 Df gilt: x1 x2 fx1 fx2 )<br />
( f heißt dann auch injektiv )<br />
(9.5) f heißt streng monoton steigend auf I , falls für alle x1, x2 I gilt :<br />
x1 x2 fx1 fx2<br />
f heißt streng monoton fallend auf I , falls für alle x1, x2 I gilt :<br />
x1 x2 fx1 fx2<br />
(nur „monoton”: , statt , )<br />
Dabei sei I Df ein (offenes, halboffenes, geschlossenes) Intervall<br />
(9.6) f streng monoton (steigend oder fallend) auf Df f umkehrbar<br />
(nur hinreichend !) Gegenbeispiel:<br />
8<br />
6<br />
4<br />
2<br />
-2 2 4 6 8<br />
-2<br />
4
Ab jetzt für die restliche Vorlesung: Entweder ist<br />
Df „ , , b , , b , a, b , a, b , a, b , a, b , a, , a, ” a, b <br />
oder Df ist eine Vereinigung von solchen Intervallen !!!<br />
(9.7) a) b heißt der Grenzwert von f für x gegen a , falls gilt:<br />
Für alle Folgen xn mit xn Df , xn a , lim xn a ist<br />
n<br />
Bezeichnung:<br />
lim fx b<br />
xa<br />
lim fxn b<br />
n<br />
(Die Definition gilt sinngemäß auch, falls a „“ oder/und b „“ )<br />
Beispiel:<br />
b) b heißt der<br />
lim<br />
xa<br />
x a wegen (8.5) c) .<br />
linksseitige<br />
rechtsseitige<br />
falls gilt: Für alle Folgen xn mit<br />
Bezeichnung:<br />
xn Df ,<br />
Grenzwert von f für x gegen a ,<br />
xn a<br />
xn a , lim xn a ist<br />
n<br />
lim fx b<br />
xa0<br />
lim fx b<br />
xa0<br />
lim fxn b<br />
n<br />
(9.8) Die reelle Funktion f heißt ( linksseitig , rechtsseitig ) stetig an der Stelle<br />
a Df , falls<br />
lim fx fa ,<br />
xa0<br />
lim fx fa <br />
xa0<br />
lim fx fa<br />
xa<br />
( Gf lässt sich dann „in der Nähe” von a, fa „ohne Absetzen” zeichnen.<br />
f ist z. B. stetig , falls fx durch einen „geschlossenen” Ausdruck<br />
(z. B. x 3 2x , sin x , e xc .....) gegeben ist. )<br />
5
Beispiele: (1) f mit fx x ist stetig (siehe Beispiel zu (9.7))<br />
(2) f : 2, 6 : x fx :<br />
x 2 3 2 x 1<br />
x 5 1 x 6<br />
f ist stetig auf 2, 6 \ 1 (rechtsseitig in 2 , linksseitig in 6 ,<br />
und unstetig in 1 :<br />
( Gf siehe (9.1) )<br />
lim fx 2 <br />
x10<br />
lim fx 4<br />
x10<br />
(9.9) Vielfache, Summen, Produkte, Quotienten, Kompositionen stetiger<br />
<strong>Funktionen</strong> sind stetig.<br />
(Bei Quotienten „verkleinert” sich evtl. der Definitionsbereich! s.o.)<br />
(9.10) a) fx0 heißt absolutes<br />
für alle x Df .<br />
b) fx0 heißt ein lokales<br />
mit x0 , x0 Df<br />
Maximum<br />
Minimum<br />
Maximum<br />
Minimum<br />
fx fx0<br />
fx fx0<br />
von f , falls<br />
fx fx0<br />
fx fx0<br />
von f in x0, falls für ein 0<br />
für alle x x0, x0 .<br />
(9.11) (Zwischenwertsatz) Sei f eine reelle stetige Funktion mit Df a, b .<br />
Dann hat f sowohl ein absolutes Maximum fxmax als auch ein<br />
absolutes Minimum fxmin , und fx nimmt auf a, b sämtliche Werte<br />
zwischen fxmin und fxmax an .<br />
(Die Abgeschlossenheit des betrachteten Intervalls ist von zentraler<br />
Bedeutung: z.B ist fx tan x stetig auf dem offenen Intervall , ,<br />
2 2<br />
hat aber dort weder Minimum noch Maximum.)<br />
6
a b<br />
7
(9.12) Exponentialfunktion und natürlicher Logarithmus.<br />
a) expx : ex lim1<br />
<br />
n x n n <br />
xk k!<br />
k0<br />
e x 0 für alle x e xx<br />
e x e x<br />
lim<br />
x e x lim<br />
x e x 0<br />
, x <br />
e x ist streng monoton steigend ( exp ist umkehrbar)<br />
b) ln x : log e x , x : x / x 0 .<br />
Es ist exp 1 x ln x , d.h. exp exp 1 x e lnx x , x ,<br />
bzw. exp 1 expx ln e x x , x .<br />
lnx1 x2 ln x1 ln x2 ln x1<br />
x2 ln x1 ln x2 ln x ln x<br />
lim<br />
x ln x lim<br />
x0 ln x <br />
ln x ist streng monoton steigend<br />
y<br />
8<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
-4 -3 -2 -1 1 2 3 4 5 6 7 8<br />
-1<br />
-2<br />
-3<br />
-4<br />
x<br />
8
c) Allgemeine Exponentialfunktion: a 0 : Ax a x : e xlna , x <br />
1<br />
2 x e x e x 2 x<br />
<br />
7<br />
6<br />
5<br />
4<br />
3<br />
2<br />
1<br />
A 1 x log a x 1<br />
ln a ln x , x .<br />
-4 -3 -2 -1 1 2 3 4 5 6 7<br />
-1<br />
-2<br />
-3<br />
-4<br />
log 2 x<br />
ln x<br />
log 1 x<br />
2<br />
9