Kapitel 6 (fast komplett) - homepages.uni-regensburg.de

6 Gewöhnliche Differentialgleichungen
6.1 Einleitung
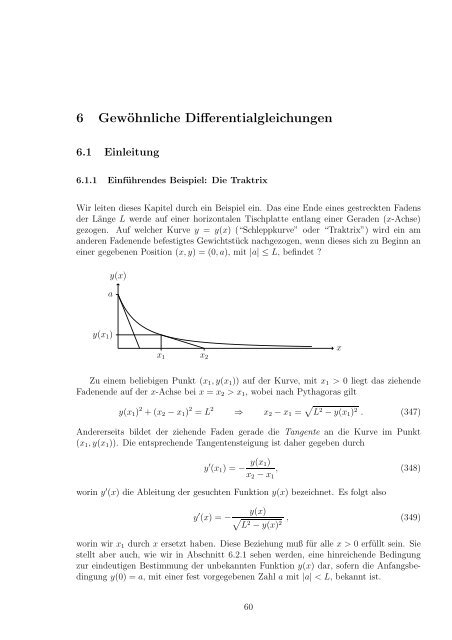
6.1.1 Einführendes Beispiel: Die Traktrix
Wir leiten dieses Kapitel durch ein Beispiel ein. Das eine Ende eines gestreckten Fadens
der Länge L werde auf einer horizontalen Tischplatte entlang einer Geraden (x-Achse)
gezogen. Auf welcher Kurve y = y(x) (“Schleppkurve” oder “Traktrix”) wird ein am
anderen Fadenende befestigtes Gewichtstück nachgezogen, wenn dieses sich zu Beginn an
einer gegebenen Position (x, y) = (0, a), mit |a| ≤ L, befindet ?
y(x)
a
y(x1)
x1
x2
Zu einem beliebigen Punkt (x1, y(x1)) auf der Kurve, mit x1 > 0 liegt das ziehende
Fadenende auf der x-Achse bei x = x2 > x1, wobei nach Pythagoras gilt
y(x1) 2 + (x2 − x1) 2 = L 2
⇒ x2 − x1 = L 2 − y(x1) 2 . (347)
Andererseits bildet der ziehende Faden gerade die Tangente an die Kurve im Punkt
(x1, y(x1)). Die entsprechende Tangentensteigung ist daher gegeben durch
y ′ (x1) = − y(x1)
x2 − x1
x
, (348)
worin y ′ (x) die Ableitung der gesuchten Funktion y(x) bezeichnet. Es folgt also
y ′ y(x)
(x) = −
, (349)
L2 − y(x) 2
worin wir x1 durch x ersetzt haben. Diese Beziehung muß für alle x > 0 erfüllt sein. Sie
stellt aber auch, wie wir in Abschnitt 6.2.1 sehen werden, eine hinreichende Bedingung
zur eindeutigen Bestimmung der unbekannten Funktion y(x) dar, sofern die Anfangsbedingung
y(0) = a, mit einer fest vorgegebenen Zahl a mit |a| < L, bekannt ist.
60

6.1.2 Allgemeine Definition
Gl. (349) ist eine sog. Differentialgleichung, da sie eine Beziehung zwischen einer gesuchten
Funktion y(x) und deren Ableitung y ′ (x) herstellt. Aus eben diesem Grund kann man
die gesuchte Funktion y(x) nicht einfach durch algebraisches “Auflösen nach y” finden.
Ehe wir Lösungsverfahren besprechen werden, wollen wir zunächst Grundbegriffe klären.
Während gewöhnliche Gleichungen, wie etwa die quadratischen Gleichung
x 2 + 4x + 13 = 0, (350)
Zahlen als Lösungen haben (hier: x1,2 = −2 ± 3 i ), wird eine Differentialgleichung (DGl)
durch Funktionen gelöst. Unter einer DGl versteht man allgemein eine Beziehung zwischen
einer unbekannten (gesuchten) Funktion und einer oder mehrerer ihrer Ableitungen.
Bsp.: Hier ist eine DGl für die unbekannte Funktion y(x),
y ′′ (x) + 4y ′ (x) + 13y(x) = 0. (351)
Ihre Lösungsmenge ist eine Funktionenschar (mit zwei Scharparametern a und b),
L = y(x) = a cos(3x) + b sin(3x) e −2x
a, b ∈ R . (352)
Da in dieser DGl neben der gesuchten Funktion y(x) auch deren Ableitungen y ′ (x) und
y ′′ (x) auftreten, kann sie nicht einfach nach der Unbekannten y(x) “aufgelöst” werden,
sondern erfordert ein besonderes Lösungsverfahren.
Def.: Eine DGl heißt gewöhnlich, wenn die Unbekannte eine Funktion y(x) von nur einer
Variable x ist. Eine gewöhnliche DGl heißt von n-ter Ordnung, wenn y (n) (x) die höchste
in ihr auftretende Ableitung von y(x) ist. Gl. (351) ist also eine DGl zweiter Ordnung.
Dagegen ist die Gleichung der Traktrix von erster Ordnung.
Bem.: Ist die Unbekannte einer DGl eine Funktion von mehreren Variablen, so spricht
man von einer partiellen DGl. Ein Beispiel ist die Wellengleichung
1
c2 ∂2y(x, t)
∂t2 6.1.3 Zwei besonders einfache, aber wichtige DGlen
= ∂2y(x, t)
∂x2 . (353)
Bevor wir uns systematischen Lösungsverfahren zuwenden, sollen zwei wichtige DGlen,
deren Lösungsmengen leicht zu erraten sind, vorweggenommen werden. Es handelt sich
um lineare DGlen mit konstanten Koeffizienten, siehe Abschnitt 6.4.4.
61

Eine DGl erster Ordnung für die gesuchte Funktion N(t) ist die Wachstumsgleichung,
˙N(t) = λN(t) (λ > 0). (354)
Die Variable t ist meistens die Zeit. (Ableitungen nach t werden mit einem Punkt bezeichnet.)
Die sog. Wachstumskonstante λ muß aus Dimensionsgründen die Einheit s −1 haben.
Die allgemeine Lösung dieser DGl lautet
N(t) = N0e λt
(N0 ∈ R). (355)
Wie es sein muss, ist der Exponent λt für jeden Wert von t eine dimensionslose Zahl.
N(t) könnte etwa die (näherungsweise als kontinuierlich angenommene) Anzahl der
Individuen einer Bakterienkolonie sein, die sich ungehindert vermehren kann. Dann ist
die frei wählbare Integrationskonstante N0 gleich der Anzahl der Individuen zur Zeit t = 0,
und die Wachstumsgleichung bringt das Gesetz zum Ausdruck, daß die Wachstumsrate
˙N(t) stets der momentanen Population N(t) proportional ist. Dann isi T = 1 gerade die
λ
Zeit, während der sich die Population um den Faktor e ≈ 2.72 vermehrt.
Das Zerfallsgesetz ergibt sich, wenn man ein Minuszeichen einführt,
˙N(t) = −λN(t) (λ > 0) ⇒ N(t) = N0e −λt
Die mittlere Lebensdauer τ ergibt sich aus
τ = 1
∞ ∞
dt N(t) = dt e −λt −λt e
∞ =
λ 0
N0
0
0
(N0 ∈ R).. (356)
= 1
. (357)
λ
Eine DGl zweiter Ordnung für die gesuchte Funktion x(t) ist die Oszillatorgleichung,
m¨x(t) = −kx(t) (k > 0), (358)
mit der Masse m und der Kraftkonstante k (Einheit: N/m = kg/s 2 ). Mit der Frequenz
ω = k/m (359)
ist die allgemeine Lösung der Oszillatorgleichung gegeben durch
x(t) = a cos(ωt) + b sin(ωt) ≡ A cos(ωt − φ) (a, b ∈ R), (360)
mit zwei frei wählbaren Integrationskonstanten a = A cosφ und b = A sin φ. Damit lassen
sich die Anfangsbedingungen x(0) = x0 und ˙x(0) = v0 erfüllen,
a = x0, b = v0
. (361)
ω
Die DGl der Traktrix ist nicht von dieser einfachen Sorte. Sie läßt sich aber auch mit
einem einfachen Verfahren lösen, das wir jetzt behandeln werden.
62

6.2 DGlen erster Ordnung: Trennung der Variablen
Viele DGlen erster Ordnung lassen sich durch “Trennung der Variablen” lösen. Dieses
Verfahren wird hier am Beispiel der Traktrix-Gleichung erläutert. Zwei weitere Anwendungsbeispiele
folgen. (Als Gegenbeispiel, das diesem Verfahren nicht zugänglich ist,
erwähnen wir die inhomogenen linearen DGlen erster Ordnung aus Abschnitt 6.4.2.)
6.2.1 Lösung der Traktrix-Gleichung
Die spezielle DGl der Traktrix besitzt die allgemeine Form
f y(x) y ′ (x) = g(x), (362)
mit zwei vorgegebenen Funktionen f(y) und g(x), hier
a2 − y2 f(y) = ,
y
g(x) ≡ −1. (363)
Gl. (362) heißt eine DGl mit getrennten Variablen. Sei nämlich f(y) = F ′ (y) und g(x) =
G ′ (x). Dann ist y(x) offenbar eine Lösung der DGl (362), wenn gilt
F y(x) = G(x) + C (C ∈ R, beliebig). (364)
Ist F(y) zudem explizit invertierbar, so folgt direkt
y(x) = F −1 G(x) + C
(C ∈ R). (365)
Dies ist eine ganze Schar (mit C als Parameter) von Lösungen der DGl (362)!
Bsp. 1: Für die DGl der Traktrix haben wir die Stammfunktionen
F(y) = a ln a + a 2 − y 2
y
− a 2 − y 2 , G(x) = −x. (366)
Die Funktion F(y) ist zwar nicht explizit invertierbar, aber die inverse Funktion existiert,
und man kann die exakte Lösung graphisch darstellen.
Merkregel (Trennung der Variablen): Läßt sich eine DGl auf die Form
bringen [wobei y ′ (x) = dy
dx
f(y) dy = g(x) dx (367)
formal als Quotient behandelt wird], dann erhält man durch
formale Integration beider Seiten
F(y) + C1 = G(x) + C2 ⇒ y = F −1
G(x) + C1 + C2
C
(368)
63

6.2.2 Spiralbahn im klassischen Modell des Wasserstoffatoms
Im klassischen Modell des Wasserstoffatoms würde das Elektron (mit Masse m und
Ladung −e) auf einer Kreisbahn mit gegebenem Radius r mit jener Geschwindigkeit
v = v(r) um das Proton laufen, bei der sich Zentrifugal- und Zentripetalkraft gerade
kompensieren. Mehr als v interessiert hier der Betrag a = a(r) des daraus resultierenden,
zum Kreiszentrum hin weisenden Vektors a der (Zentripetal-) Beschleunigung,
a(r) ≡ v2 |FCoul| 1 e
= ≡
r m 4πǫ0
2
mr2. (369)
Als beschleunigte Ladung müsste dieses Elektron ständig elektromagnetische Wellen aussenden.
Nach der Larmor-Formel betrüge die abgestrahlte Leistung
P(r) ≡ 1 2e
4πǫ0
2
3c2 a(r)2 1
=
(4πǫ0) 3
2e6 3m2c3 1
r4. (370)
Mit dieser Rate müsste die gesamte (kinetische plus potentielle) Energie des Elektrons,
E(r) = m
2 v2 − 1 e
4πǫ0
2
r
1 e
= −
4πǫ0
2
, (371)
2r
kontinuierlich abnehmen. Als Folge würde auch der Bahnradius r abnehmen, r = r(t),
mit Ableitung ˙r(t) < 0. Für den Bohr-Radius r = rB = 4πǫ0 e2 schätzen wir die während
c
abgestrahlte Energie ∆E ab durch
einer entsprechenden Umlaufszeit T(rB) = 2πrB
v(rB)
∆E ≈ P(rB) T(rB) = 4π
3
(Hier ist α = e2 /4πǫ0(c) ≈ 1
137
α2 (c/rB) 3
(mc 2 ) 2 = 10−17 eV ≪ E(rB) . (372)
die Feinstrukturkonstante.) Da dies nur ein winziger
Bruchteil der Gesamtenergie E(rB) = −13.6 eV ist, ist zu erwarten, daß die Abnahme
des Bahnradius pro Umlauf sehr gering, die Bahn also sehr gut durch eine Kreisbahn mit
kontinuierlich aber langsam abnehmendem Radius r(t) angenähert wird. Wir setzen also
P r(t) = − d
dt E r(t) ≡ −E ′ r(t) ˙r(t) ≡ − 1
4πǫ0
e2 ˙r(t). (373)
2r(t) 2
Hier haben wir die Ableitung E ′ (r) der Funktion (371) eingesetzt. Mit Gl. (370) wird
daraus eine gewöhnliche DGl für die gesuchte Funktion r(t),
˙r(t) = − b
r(t) 2,
b :=
1
(4πǫ0) 2
4e 4
3m 2 c
3 = 3.17 × 10−21m3
Nach Trennung der Variablen, r 2 dr = −b dt, ergibt Integration
s
. (374)
r 3
3 + C1 = −bt + C2 ⇒ r(t) = 3(C2 − C1) − bt ≡ b(tf − t). (375)
Die Integrationskonstante tf wird festgelegt durch den Anfangswert r(0) = rB,
tf = r3 B
b = 5 × 10−11 s. (376)
So lange dauert in dieser Näherung der Sturz des klassischen Elektrons in den Kern.
64

6.2.3 Die Kettenlinie
Ein Seil der Länge L sei zwischen zwei Punkten mit horizontalem Abstand B und vertikalem
Abstand H aufgehängt (L 2 > H 2 + B 2 ). Welche Funktion y(x) beschreibt das
durchhängende Seil? (x-Achse horizontal und y-Achse vertikal nach oben.)
Auf ein kurzes (leicht gekrümmtes) Seilstück der Länge δs ≪ L, mit Schwerpunkt bei
x = x0 und Endpunkten bei x = x1,2, wirken drei Kräfte: Im Schwerpunkt, senkrecht
nach unten, seine Gewichtskraft G und an den Endpunkten, jeweils in tangentialer Rich-
tung, Zugkräfte F1 bzw. F2. Da die Vektorsumme aller Kräfte verschwinden muß, gilt
0
−Fx
Fx
G = , F1 = , F2 = . (377)
−γδs
−Fy
Fy + γδs
γ ist die Wichte (Gewicht pro Längeneinheit) des Seils.
|Fx| ist die an jeder Stelle des Seils gleich große Horizontalkomponente der Seilspannung.
Da die Zugkräfte tangential an den Enden des Seilstücks angreifen, folgt
y ′ (x1) = Fy
, y ′ (x2) = Fy + γδs
, (378)
Mit δs → 0 gelten: x1 → x0 − 0 und x2 → x0 + 0. Daher folgt weiter
Fx
y ′′ y
(x0) := lim
δs→0
′ (x2) − y ′ (x1)
=
x2 − x1
γ
Fx
Fx
lim
δs→0
δs
x2 − x1
. (379)
Mit δs → 0 wird die Krümmung des Seilstücks vernachlässigbar und nach Pythagoras gilt
δs → (δx) 2 + (δy) 2 → δx 1 + y ′ (x0) 2 ⇒ x2 − x1 ≡ δx →
δs
1 + y ′ (x0) 2.(380)
Kombination der beiden letzten Beziehungen liefert (mit x0 =: x) die DGl der Kettenlinie,
y ′′ (x) = a 1 + y ′ (x) 2 , a := γ
Fx
. (381)
Sie ist eine gewöhnliche DGl erster Ordnung für die Funktion η(x) := y ′ (x). Trennung
der Variablen, dη/ 1 + η 2 = a dx, und Integration (mit Integrationskonstante C) ergibt
arcsinh(η) = a(x − C), C ∈ R. (382)
Inversion, η(x) = sinh(a(x − C)) ≡ y ′ (x), und erneute Integration ergibt schließlich
y(x) = 1
a cosh a(x − C) + C ′ , C, C ′ ∈ R. (383)
Die Integrationskonstante C ′ legt den Nullpunkt der y-Achse fest, spielt also keine Rolle.
C und die horizontale Seilspannung Fx = a/γ ergeben sich aus den beiden Gleichungen
L =
B
δs = dx
0
1 + y ′ (x) 2 = 1
B
dxy
a 0
′′ (x) = y′ (B) − y ′ (0)
,
a
(384)
H = y(B) − y(0). (385)
65

6.3 Eindimensionale Bewegungsgleichungen
6.3.1 Definition
Bewegt sich ein Punktteilchen der Masse m längs einer vorgegebenen glatten Kurve, so ist
seine (von einem willkürlich gewählten Anfangspunkt an) entlang der Kurve gemessene
Bogenlänge s eine zweimal differenzierbare Funktion s(t) der Zeit t. Die zweite Ableitung
¨s(t) heißt die (Tangential-) Beschleunigung des Teilchens entlang der Kurve. Nach dem
Zweiten Newtonschen Gesetz gilt zu jeder Zeit t die sog. Bewegungsgleichung (BGl)
m¨s(t) = F(t), (386)
wobei F(t) die Tangential-Komponente der zur Zeit t auf das Teilchen wirkenden Kraft
F(t) (in positiver s-Richtung entlang der Kurve) ist.
Ist die Funktion F(t) von vorneherein bekannt, so findet man die gesuchte Bewegungsfunktion
s(t) des Teichens durch zwei elementare Integrationen,
t
˙s(t) = v0 +
t0
dτ 1
m F(τ), s(t) = s0 +
t
dτ ˙s(τ). (387)
Die Anfangswerte s0 := s(t0) bzw. v0 := ˙s(t0) für Ort und Geschwindigkeit zum Anfangszeitpunkt
t = t0 sind frei wählbare Integrationskonstanten. Als Beispiel betrachten
wir ein Teilchen mit Masse m und Ladung q (im schwerelosen Raum) zwischen den Platten
eines Kondensators mit vorgegebenem zeitlich variierenden Feld E(t) = E0 cos(ωt).
Bewegt sich das Teilchen in x-Richtung (senkrecht zu den Platten), so lautet seine BGl
t0
m¨x(t) = qE0 cos(ωt). (388)
Durch direkte Integration findet man ihre allgemeine Lösung,
x(t) = x0 + v0t − qE0
cos(ωt). (389)
mω2 In den meisten Fällen ist aber die Funktion F(t) nicht von vorneherein bekannt. Dann
stellt die Bewegungsgleichung eine echte DGl dar. Dies soll ein Beispiel demonstrieren.
Bsp. (Fadenpendel): Eine Punktmasse m sei im Schwerefeld der Erde an einem Faden
der Länge ℓ aufgehängt und führe Pendelschwingungen in der xz-Ebene aus (z-Richtung
nach oben). Die Bahn der Mase m ist offenbar eine vertikale Kreislinie in der xz-Ebene
mit Radius ℓ. Der Gleichgewichtslage (also dem tiefstem Punkt) dieser Bahn wählen
wir als Nullpunkt der Bogenlänge s. Ist das Pendel um den Winkel φ aus der Verikalen
ausgelenkt, so befindet sich die Masse bei der Bogenlänge s = ℓφ (mit φ, s > 0 für x > 0).
66

z
m
Die Komponente F(t) der auf die Masse einwirkenden Kraft in Richtung tangential
zur Bahn ist die entsprechende Komponente der Gewichtskraft G = −mgez,
x
F(t) = −mg sin φ ≡ −mg sin s
. (390)
ℓ
(Außer G wirkt zwar auch eine Seilzugkraft auf das Teilchen, doch die trägt nicht zur
tangentialen Komponente der Gesamtkraft bei.) F(t) ist also nicht explizit als Funktion
von t gegeben, sondern implizit als Funktion F(s) der zeitabhängigen Bogenlänge s = s(t),
F(t) = F s(t) , F(s) = −mg sin s
. (391)
ℓ
Um also die rechte Seite F(t) der Bewegungsgleichung explizit angeben zu können, müsste
man deren Lösung s(t) bereits kennen! Sie ist jetzt also eine echte DGl.
m¨s(t) = −mg sin s(t)
. (392)
ℓ
Sie muß von der gesuchten Funktion s(t) und ihrer zweiten Ableitung ¨s(t) zu jeder Zeit t
erfüllt sein. Wir werden diese DGl zweiter Ordnung im folgenden Abschnitt lösen.
Def.: Unter der Bewegungsgleichung (BGl) eines Teilchens versteht man die DGl
m¨s(t) = F s(t), ˙s(t), t ≡ F(t). (393)
Dabei ist F(t) die Komponente der auf das Teilchen zur Zeit t wirkenden Kraft tangential
zur Bahn (in positiver s-Richtung). Sie ist selten als explizite Funktion F(t) = F(t)
der Zeit t gegeben. Meistens ist sie eine Funktion F(t) = F(s(t)) des Ortes s = s(t),
gelegentlich eine Funktion F(t) = F(s(t), t), die explizit von Ort s und Zeit t abhängt.
Ein wichtiger Sonderfall ist eine (zusätzliche) explizite Abhängigkeit F(t) = F(s(t), ˙s(t), t)
von der Geschwindigkeit ˙s(t), siehe Abschnitt 6.3.3.
67

Bem.: Ehe wir die exakte Lösung der BGl des Fadenpendels untersuchen, wollen wir sie
im Grenzfall kleiner Auslenkungen |s(t)| ≪ ℓ näherungsweise lösen. In diesem Fall gilt
sin s(t)
ℓ
s(t)
≈ , (394)
ℓ
und wir erhalten die lineare DGl m¨s(t) = −mgs(t)/ℓ bzw.
¨s(t) = −ω 2 s(t),
g
ω := ,
ℓ
(395)
mit der Lösung s(t) = A cos(ωt) (A ≪ ℓ). Die Schwingungsperiode
T = 2π
ℓ
= 2π
ω g
(396)
ist in diesem Grenzfall unabhängig von der Amplitude A. Dies ist bei größeren Amplituden
nicht der Fall. Im Grenzfall A → πℓ, wenn das Pendel (dessen Faden durch einen starren,
gewichtslosen Stab ersetzt ist) zu Beginn nahezu senkrecht nach oben zeigt, gilt sogar
T → ∞.
6.3.2 Energieerhaltung
Bewegungsgleichungen sind DGlen zweiter Ordnung für die gesuchte Bewegungsfunktion
s(t). Häufig lassen sie sich jedoch auf eine DGl erster Ordnung für s(t) zurückführen.
Dies ist immer dann der Fall, wenn die Kraft eine explizite Funktion nur des Orts s ist,
F(t) = F(s(t)). (397)
Die bis auf eine willkürliche Konstante V (s0) festgelegte negative Stammfunktion V (s),
s
V (s) = V (s0) −
s0
d s ′ F(s ′ ) ⇔ F(s) = − d
ds V (s) ≡ −V ′ (s), (398)
heißt in diesem Fall die (ortsabhängige) potentielle Energie des Teilchens am Ort s seiner
Bahn. Um ihre Bedeutung zu erkennen, berechnen wir die zeitliche Ableitung dieser
Größe während das Teilchen sich bewegt,
d
dt V s(t) = V ′ s(t) ˙s(t) = −F s(t) ˙s(t). (399)
Hier wurde im ersten Schritt die Kettenregel und im zweiten die Definition der Funktion
V (s) benutzt. Mit der Bewegungsgleichung, F s(t) = m¨s(t), folgt schließlich
d
dt V s(t) = −m¨s(t) ˙s(t) ≡ d
−
dt
m
2 ˙s(t)2
. (400)
68

Dieses Ergebnis besagt offenbar, daß die Größe
E := V s(t) + m
2 ˙s(t)2 = const, (401)
genannt die mechanische (Gesamt-) Energie des Teilchens, während seiner Bewegung
zeitlich konstant bleibt. Der geschwindigkeitsabhängige, “nicht-potentielle”, Teil davon
heißt seine kinetische Energie,
Ekin := m
2 ˙s2 ≡ m
2 v2 ≡ Ekin(˙s). (402)
Anders als die Masse m, die Geschwindigkeit v, etc. ist die Energie E keine anschauliche,
“direkt meßbare” Größe. Sie wird nur deshalb thematisiert, weil für sie der soeben
aufgezeigte Erhaltungssatz gilt. Sie ist eine Konstante der Bewegung.
Der Nutzen der Konstante E wird klar, wenn wir Gl. (401) nach ˙s(t) auflösen,
2
˙s(t) = E − V
m
s(t)
. (403)
Dies ist eine DGl erster Ordnung für s(t), die durch Trennung der Variablen lösbar ist,
dt =
2
m
ds
⇒ t =
E − V (s)
m
2
Bsp.: Im Fall des Fadenpendels aus Abschnitt 6.3.1 haben wir
F(s) = −mg sin s
ℓ
s
s0
ds ′
E − V (s ′ ) + t0. (404)
⇒ V (s) = −mgℓ cos s
. (405)
ℓ
Es gilt also V (s) = mgz, mit der “Höhe“ z = ℓ cos(s/ℓ) der Masse m im Schwerefeld
(Ursprung der xz-Ebene im Aufhängepunkt des Pendels). Könnte man das Integral
t1 =
m
2
s1
s0
ds
E + mgℓ cos s
ℓ
φ1 ℓ
≡
2g
φ0
dφ
E + cosφ
mgℓ
(406)
explizit auswerten, so erhielte man durch Inversion der resultierenden Stammfunktion die
gesuchte Bewegungsfunktion s(t). Bei der Maximalauslenkung φ = α = A/ℓ muß wegen
V (A) = E der Nenner des Integranden verschwinden,
E
mgℓ = − cosα, t1
=
ℓ
2g
69
φ1
φ0
dφ
√ cosφ − cosα . (407)

Die Schwingungsperiode T ist das 4-fache der Zeit zwischen Maximalauslenkung φ = α
und anschließender Tiefstlage φ = 0,
α
ℓ dφ
ℓ
T(α) = 4 √ =: 2π ξ(α) . (408)
2g cosφ − cosα g
Für kleine Auslenkungen |φ| ≤ α ≪ π folgt mit cosx ≈ 1 − 1
2 x2
0
0
α
ℓ dφ ℓ
T(α) ≈ 4 = 4 arcsin
g α2 − φ2 g
φ
α ℓ
= 2π . (409)
α 0 g
Für α → 0 gilt also f(α) → 1. Für endliche α > 0 kann das Integral
√ α
2 dφ
f(α) = √
π cosφ − cos α
0
auf ein elliptisches Integral zurückgeführt werden. Eine numerische Auswertung ergibt
(TABELLE)
6.3.3 Dissipation
(410)
Unter Dissipation versteht man die Umwandlung von mechanischer Energie in Wärme.
Ein einfaches Beispiel ist der gedämpfte harmonische Oszillator, bei dem neben der
Rückstellkraft −kx(t) eine geschwindigkeits-proportionale Reibungskraft −γ ˙x(t) wirkt,
Die resultierende BGl,
F(t) = −kx(t) − γ ˙x(t) = F x(t), ˙x(t) . (411)
m¨x(t) + γ ˙x(t) + kx(t) = 0, (412)
läßt sich nicht auf eine DGl erster Ordnung zurückführen.
Im Gegensatz zur BGl des Fadenpendels ist diese DGl aber linear und damit zugänglich
für eine völlig andere Lösungsmethode.
70

6.4 Lineare DGlen
6.4.1 Allgemeine Definition
Def.: Sei I = (x1, x2) ⊆ R ein offenes Intervall. Eine lineare DGl n-ter Ordnung für die
gesuchte Funktion y : I → R, x ↦→ y(x) hat die Form
y (n) n−1
(x) + ak(x)y (k) (x) = b(x), (413)
k=0
mit reellwertigen und auf I stetigen Koeffizientenfunktionen ak(x) und b(x).
Im Fall b(x) ≡ 0 heißt die lineare DGl homogen, andernfalls heißt sie inhomogen.
Bsp.: Eine inhomogene ineare DGl dritter Ordnung ist etwa
y ′′′ (x) + x 2 y ′′ (x) + sin x y ′ (x) + x 2 + 2x + 3 y(x) = √ x, (414)
mit den Koeffizientenfunktionen
a2(x) = x 2 , a1(x) = sin x, a0(x) = x 2 + 2x + 3, b(x) = √ x. (415)
Dagegen sind die drei folgenden DGlen nicht linear,
y ′ (x) + y(x) = 0, y ′ (x) 2 + y(x) = x, ¨s(t) + g sin s(t)
ℓ
= 0. (416)
Bem.: Eine besondere Eigenschaft homogener linearer DGlen ist:
Sind die Funktionen y1(x) und y2(x) Lösungen, so ist auch jede Linearkombination
y(x) = c1y1(x) + c2y2(x) (c1, c2 ∈ R), (417)
mit beliebigen Konstanten c1, c2 ∈ R, eine Lösung.
Sind dagegen y1,2(x) Lösungen einer inhomogenen linearen DGl, so ist die Differenz
eine Lösung der zugehörigen homogenen DGl.
y(x) = y1(x) − y2(x) (418)
Ehe wir das allgemeine Lösungsverhalten linearer DGlen untersuchen, wollen wir den
einfachsten Fall erster Ordnung gesondert betrachten.
71

6.4.2 Lineare DGlen erster Ordnung
Eine lineare DGl erster Ordnung für die gesuchte Funktion y : I → R, x ↦→ y(x),
y ′ (x) + a(x)y(x) = b(x), (419)
hat zwei reellwertige auf I stetige Koeffizientenfunktionen a(x) und b(x).
Im homogenen Fall b(x) ≡ 0 ist sie immer durch Trennung der Variablen lösbar,
dy
dx
= −a(x)y ⇒
dy
y
= −a(x)dx. (420)
Integriert man beide Seiten der letzten Gleichung und erhebt sie dann zur Potenz von e,
so erhält man die Lösungsschar
y(x) = c e −A(x)
(c ∈ R), (421)
Hier bezeichnet A(x) eine beliebige Stammfunktion des Koeffizienten a(x),
A ′ (x) = a(x). (422)
Wie wir sehen werden, ist diese Schar bereits die vollständige Lösungsmenge.
Bsp.: Der Koeffizient a(x) = − k
x
ergibt die homogene DGl
y ′ (x) − k
x y(x) = 0 ⇔ y′ (x) = k y(x)
x
(423)
mit der Lösungsmenge
L = y(x) = ce k lnx ≡ c x k
c ∈ R . (424)
Eine ähnliche DGl ist
mit der Lösungsmenge
L =
y ′ (x) − kxy(x) = 0 (425)
y(x) = c e k x2 /2
c ∈ R . (426)
Satz: Die allgemeine Lösung der inhomogenen linearen DGl erster Ordnung ist
y(x) = e −A(x)
x
c + dt b(t) e A(t)
(c ∈ R), (427)
Zum Beweis: Mit der Produktregel sieht man direkt
x0
y ′ (x) = −a(x) y(x) + e −A(x) b(x) e A(x) = −a(x) y(x) + b(x), q.e.d. (428)
Bem.: Gl. (427) wird auch als Variation der Konstanten in Gl. (421) bezeichnet. Ersetzt
man nämlich dort die Konstante c durch eine Funktion c(x) und fordert, daß die
resultierende Funktion y(x) Lösung der inhomogenen DGl mit b(x) = 0 wird, erhält man
Gl. (427).
72

6.4.3 Der Lösungsraum einer homogenen linearen DGl
Def.: Ein Satz von n Funktionen fk : I → R, x ↦→ fk(x) (k = 1, ..., n) heißt linear
abhängig, wenn diese eine nicht-trivale Darstellung der Nullfunktion ermöglichen,
c1f1(x) + ... + cnfn(x) = 0 ∀ x ∈ I,
n
|ck| > 0. (429)
Satz: Die Lösungsmenge einer homogenen linearen DGl n-ter Ordnung bildet einen ndimensionalen
Vektorraum. M. a. W.: Sind n linear unabhängige Lösungen yk(x) bekannt
(k = 1, ..., n), so ist die Gesamtheit aller Lösungen y(x) gegeben durch
Bsp.:
y(x) =
k=1
n
ckyk(x) (c1, ..., cn ∈ R). (430)
k=1
Korollar: Ist y0(x) irgendeine Lösung einer inhomogenen linearen DGl n-ter Ordnung,
so ist die Gesamtheit aller Lösungen gegeben durch
y(x) = y0(x) +
n
ckyk(x) (c1, ..., cn ∈ R), (431)
k=1
wobei y1(x), ..., yn(x) linear unabh. Lösungen der zugehörigen homogenen DGl sind.
Zum Beweis: Die Differenz zweier verschiedener Lösungen der inhomogenen DGl ist offenbar
immer eine Lösung der homogenen DGl!
73

6.4.4 Lineare DGlen mit konstanten Koeffizienten
Wir wollen hier die unabhängige Variable mit t (statt mit x) bezeichnen.
Sind die Koeffizientenfunktionen ak(t) ≡ ak Konstanten,
y (n) n−1
(t) + aky (k) (t) = b(t), (432)
so spricht man von einer linearen DGl mit konstanten Koeffizienten.
(a) Vorbemerkung: Komplexe Funktionen einer reellen Variable
k=0
Mit zwei rellen Funktionen u, v : I → R wird durch
y(t) = u(t) + i v(t) (433)
eine komplexwertige Funktion y : I → C einer reellen Variable t ∈ I definiert.
Bem. 1: Interpretiert man t als die Zeit, so beschreibt y(t) den Ortsvektor eines Punktes,
der sich durch die komplexe Zahlenebene “bewegt“ (SKIZZE).
Sind u und v differenzierbar, mit den Ableitungen ˙u(t) bzw. ˙v(t), so definiert man
y(t + ∆t) − y(t)
˙y(t) := lim
∆t→0
∆t
u(t + ∆t) + i v(t + ∆t) − u(t) + i v(t)
= lim
∆t→0
= lim
∆t→0
∆t
u(t + ∆t) − u(t) + i v(t + ∆t) − v(t)
Entsprechend wird die k-te Ableitung von y(t) definiert,
∆t
≡ ˙u(t) + i ˙v(t). (434)
y (k) (t) := u (k) (t) + i v (k) (t). (435)
Bem. 2: Die Zahl ˙y(t), gedeutet als Vektor in der Zahlenebene, zeigt in Richtung tangential
zur Bahnkurve im Punkt y(t). Der Betrag | ˙y(t)| entspricht genau der Geschwindigkeit.
Bsp.: Mit der komplexen Konstanten µ = λ + i ω (λ, ω ∈ R) gilt
y(t) := e µt = e λt e i ωt = e λt cos(ωt) + i sin(ωt) = u(t) + i v(t), (436)
mit den reellen Funktionen
u(t) = e λt cos(ωt), v(t) = e λt sin(ωt). (437)
74

Die entsprechende Bahnkurve in der Zahlenebene ist eine nach außen (λ > 0) oder nach
innen (λ < 0) gewundene Spirale um den Ursprung. Die Ableitung dieser Funktion ist
˙y(t) = ˙u(t) + i ˙v(t) = λu(t) − ωv(t) + i λv(t) + ωu(t) . (438)
Man kann dafür auch schreiben
d
dt eµt = (λ + i ω) u(t) + i v(t) = µe µt . (439)
Es gilt also die aus dem Reellen bekannte Ableitungsregel. Allgemein gilt
(b) Homogene DGlen mit konstanten Koeffizienten
y (k) (t) ≡ dk
dt k eµt = µ k e µt . (440)
Für eine homogene DGl mit reellen (konstanten) Koeffizienten ak,
y (n) n−1
(t) + aky (k) (t) = 0, (441)
k=0
sei eine komplexe Lösung y(t) = u(t) + i v(t) gegeben,
n−1
(n) (n) (k) (k)
u (t) + i v (t) + ak u (t) + i v (t) = 0. (442)
Wegen ak ∈ R ergibt Trennung von Real- und Imaginärteil die Gleichung
u (n) n−1
(t) +
k=0
k=0
aku (k)
(t) + i v (n) n−1
(t) +
k=0
akv (k)
(t) = 0. (443)
Da die Terme in eckigen Klammern reell sind, müssen sie beide einzeln verschwinden.
Der komplexe Ansatz liefert also zwei reelle Lösungen u(t) und v(t) der homogenen DGl.
Bsp. 1: Für die DGl
machen wir den komplexen Ansatz
y(x) = e µt
¨y(x) − 6 ˙y(x) + 34 y(x) = 0. (444)
⇒ ˙y(t) = µe µt , ¨y(t) = µ 2 e µt . (445)
Einsetzen in die DGl führt wegen e µt = 0 auf eine algebraische Gleichung für µ
(µ 2 − 6µ + 34)e µt = 0 ⇔ µ 2 − 6µ + 34 = 0. (446)
75

Mit deren beiden Lösungen
erhalten wir zwei verschiedene komplexe Lösungen der DGl,
y1(t) = e µ1t = e 3t cos(5t) + i sin(5t) ,
µ1,2 = 3 ± 5 i (447)
y2(t) = e µ1t = e 3t cos(−5t) + i sin(−5t) ≡ e 3t cos(5t) − i sin(5t) , (448)
also drei verschiedene reelle Lösungen,
x1(t) = e 3t cos(5t), x2(t) = e 3t sin(5t), x3(t) = −e 3t sin(5t). (449)
Wie es sein muß, können maximal zwei davon linear unabhängig sein, etwa {x1(t), x2(t)}.
Daher ist die allgemeine reelle Lösung gegeben durch
y(t) = c1x1(t) + c2x2(t) ≡ e 3t c1 cos(5t) + c2 sin(5t)
(c1, c2 ∈ R). (450)
Bem.: Dieses Beispiel läßt sich leicht verallgemeinern: Der komplexe Ansatz
y(t) = e µt
(µ = λ + i ω; λ, ω ∈ R) (451)
führt durch Einsetzen in die homogene DGl n-ter Ordnung auf die algebraische Gleichung
µ n + an−1µ n−1 + ... + a1µ + a0 = 0 (452)
für die Unbekannte µ. Nach dem Fundamentalsatz der Algebra hat diese Gleichung n
(nicht notwendigerweise verschiedene) Lösungen
µk = λk + i ωk (λk, ωk ∈ R; k = 1, ..., n). (453)
Durch Lösen einer algebraischen Gleichung finden wir also n (nicht notwendigerweise
verschiedene) komplexe Lösungen
yk(t) = e µkt = uk(t) + i vk(t) (k = 1, ..., n), (454)
und damit 2n (nicht notwendigerweise verschiedene) reelle Lösungen der homogenen DGl,
uk(t) = e λkt cos(ωkt), vk(t) = e λkt sin(ωkt) (k = 1, ..., n). (455)
Bilden n dieser 2n reellen Lösungen einen linear unabhängigen Satz {x1(t), ..., xn(t)}, so
ist die allgemeine Lösung der DGl gegeben durch
x(t) = c1x1(t) + ... + cnxn(t) (c1, .., cn ∈ R). (456)
Ein Beispiel soll zeigen, daß dies nicht immer der Fall ist.
76

Bsp. 2: In der DGl
führt der Ansatz y(t) = e µt auf die algebraische Gleichung
¨y(t) − 4 ˙y(t) + 4 y(t) = 0 (457)
µ 2 − 4µ + 4 ≡ (µ − 2) 2 = 0 ⇒ µ1 = µ2 = 2 (458)
und liefert somit nur eine komplexe Lösung, die außerdem ”nur” reell ist,
y1(t) = e 2t = x1(t). (459)
Es muß also eine zweite reelle Lösung geben, die nicht von der Form e λt ist. Durch Raten
findet man
und die allgemeine Lösung ist
x2(t) = te 2t , (460)
x(t) = c1x1(t) + c2x2(t) = (c1 + c2t)e 2t . (461)
Bsp. 3 (Gedämpfter Oszillator): Wir betrachten die DGl
mit den dimensionsbehafteten Koeffizienten
m¨y(t) + γ ˙y(t) + ky(t) = 0, (462)
m = 0.5 kg, γ = 0.1 kg s −1 , k = 0.25 kg s −2 . (463)
Entsprechend haben jetzt y, ˙y und ¨y die Dimensionen m, m s−1 bzw. m s−2 .
Der Ansatz y(t) = y0e µt führt auf die Gleichung mµ 2 + γµ + k = 0, mit den Lösungen
µ1,2 = −γ ± γ 2 − 4km
2m
= − γ
2m ±
γ
2 −
2m
k
m
= −λ ± i ω (464)
und den Werten λ = 0.1 s −1 und ω = 0.7 s −1 . Die allgemeine Lösung der DGl ist
y(t) = c1e µ1t + c2e µ2t = c1e i ωt + c2e − i ωt e −λt
(c1, c2 ∈ C). (465)
Real- und Imaginärteil jeder dieser Lösungen sind jeweils zwei reelle Lösungen.
Als allgemeine reelle Lösung wählen wir (mit a, b ∈ R bzw. A, φ ∈ R)
x(t) = a cos(ωt) + b sin(ωt) e −λt = A cos(ωt − φ)e −λt . (466)
Dies ist eine gedämpfte, exponentiell abklingende Schwingung.
In der folgenden Abbildung ist φ = 0 und ω = 8λ.
77

x(t)
Für beliebige Werte der Koeffizienten m, γ und k sind drei Fälle zu unterscheiden:
1. Fall: γ 2 < 4km (Schwingfall), mit der allgemeinen reellen Lösung
x(t) = a cos(ωt) + b sin(ωt) e −λt = A cos(ωt − φ)e −λt
t
(A, φ ∈ R). (467)
Abklingkonstante λ und (Kreis-) Frequenz ω sind gegeben durch
λ = γ
,
2m
k
ω =
m −
γ
2 .
2m
(468)
2. Fall: γ 2 = 4km (aperiodischer Grenzfall), mit
und der einzigen Abklingkonstante
3. Fall: γ 2 > 4km (Kriechfall), mit
und den beiden Abklingkonstanten
x(t) = a + bt e −λt
x(t) = ae −λ1t + be −λ2t
λ1 = − γ
2m ±
(a, b ∈ R) (469)
λ = γ
. (470)
2m
(a, b ∈ R) (471)
γ
2 −
2m
k
. (472)
m
78

(c) Inhomogene DGlen
Um die allgemeine Lösung der inhomogenen DGl
y (n) n−1
(t) + aky (k) (t) = b(t) (473)
k=0
zu bestimmen, genügt es, eine einzige Lösung zu finden. Alle übrigen ergeben sich dann
durch Addition der aus Teil (b) bekannten allgemeinen Lösung der zugehörigen homogenen
DGl mit b(t) = 0. Wir beschränken uns auf eine Inhomogenität der Form
b(t) = A cos(Ωt) (A,Ω ∈ R), (474)
deren reelle Amplitude A und Frequenz Ω beliebig vorgegeben sind.
Bsp. 4 (Angetriebener, gedämpfter Oszillator): Eine physikalische DGl dieser Art
ist die BGl des (gedämpften) Oszillators mit periodischer Antriebskraft F cos(Ωt),
m¨x(t) + γ ˙x(t) + kx(t) = F cos(Ωt) (F,Ω ∈ R). (475)
Jede reelle Lösung x(t) dieser DGl ist der Realteil einer komplexen Lösung w(t) von
m ¨w(t) + γ ˙w(t) + kw(t) = Fe iΩt . (476)
[ Den Imaginärteil y(t) von w(t) verwerfen wir, denn er ist eine reelle Lösung von
m¨y(t) + γ ˙y(t) + ky(t) = F sin(Ωt). ] (477)
Wir machen nun für die komplexe DGl den komplexen Lösungsansatz
w(t) = Ce iΩt
(C ∈ C, Ω ∈ R), (478)
mit der vorgegebenen Antriebsfrequenz Ω. Gesucht ist jetzt die komplexe Amplitude C
(die sich bei einer homogenen DGl herauskürzen würde),
Die physikalische Lösung, also der Realteil von w(t),
C = A + i B = |C|e −iΦ , (479)
x(t) = Rew(t) = Re |C|e i(Ωt−Φ) = |C| cos(Ωt − Φ), (480)
beschreibt eine Schwingung mit Amplitude |C| > 0, die dem Antrieb um die Phase Φ
hinterherhinkt. Wir wollen die Größen |C| und Φ als Funktionen der Antriebsfrequenz Ω
bestimmen.
79

Mit dem Ansatz w(t) = Ce iΩt ergibt sich nach Division durch e iΩt
− mΩ 2 + i γΩ + k C = F. (481)
Die gesuchte komplexe Amplitude ist also gegeben durch
C =
F
(k − mΩ 2 ) + i γΩ ≡
F
a + i b
= F(a − i b)
a 2 + b 2 = |C|e−iΦ . (482)
Für die reelle Amplitude |C| und die Phase Φ der erzwungenen Schwingung folgt
|C| =
F
√ a 2 + b 2 =
tanΦ ≡ − tan(−Φ) = − −b
a
F
(k − mΩ 2 ) 2 + (γΩ) 2
= b
a =
= F
k
γΩ
= Γ
k − mΩ2 1
, (483)
(1 − ξ2 ) 2 + (Γξ) 2
ξ
1 − ξ 2.
Hier haben wir dimensionslose Varable für Frequenz Ω und Dämpfung γ eingeführt,
(484)
ξ := Ω
k/m , Γ := γ
√ km . (485)
Im statischen Fall Ω = 0 ergibt sich statt einer Schwingung die konstante Auslenkung
Im ungedämpften Fall γ = 0 haben wir
|C| = F
. (486)
k
|C| = F
k
1
|1 − ξ2 . (487)
|
Jetzt ergibt sich also bei der Eigenfrequenz Ω = k/m (ξ = 1) eine Resonanzkatastrophe,
γ = 0 : lim
ξ→1 |C| = ∞. (488)
In der Praxis wird diese Katastrophe durch eine endliche Dämpfung γ > 0 verhindert.
Das Resonanzmaximum liegt dann etwas unterhalb der Eigenfrequenz Ω = k/m.
Außerdem wächst bei endlichem Γ > 0 die nachhinkende Phase Φ,
ξ
Φ(ξ) = arctan Γ
1 − ξ2
+ πΘ(ξ − 1) (489)
von Φ = 0 bei ξ = 0 stetig nach Φ = π bei ξ = 1 (wobei das Argument des arctan
2
divergiert und sein Vorzeichen wechselt), und dann stetig weiter nach Φ = π bei ξ → ∞.
Dieses Verhalten geht im ungedämpften Grenzfall Γ → 0 in eine Stufenfunktion über,
0 (ξ < 1),
γ = 0 : Φ(ξ) =
(490)
π (ξ > 1).
80

|C(ξ)|
tanΦ(ξ)
Φ(ξ)
81
ξ
ξ
ξ

Zusammenfassung: Für die inhomogene lineare DGl
m¨x(t) + γ ˙x(t) + kx(t) = F cos(Ωt), (491)
mit vorgegebenen Konstanten m, γ, k, F,Ω ∈ R, haben wir eine spezielle Lösung gefunden,
xspez(t) = R cos(Ωt − Φ). (492)
Deren Amplitude R und Phase −Φ sind Funktionen der dimensionslosen Parameter
ξ := Ω
k/m , Γ := γ
√ km
für äußere Antriebsfrequenz Ω bzw. intrinsische Dämpfungskonstante γ,
R = F
k
1
, tanΦ = Γ
(1 − ξ2 ) 2 + (Γξ) 2
ξ
1 − ξ 2.
(493)
(494)
Die allgemeine Lösung ergibt sich durch Addition der allgemeinen Lösung der entsprechenden
homogenen DGl (mit F = 0; wir betrachten hier den Schwingfall γ 2 < 4km),
xallg(t) = R cos(Ωt − Φ) + a cos(ωt) + b sin(ωt) e −λt
(a, b ∈ R). (495)
Unabhängig von der äußeren Antriebsfrequenz Ω sind die Eigenfrequenz ω des Oszillators
und seine dämpfungsbedingte Abklingkonstante λ gegeben durch
k
ω =
m −
γ
2 , λ =
2m
γ
. (496)
2m
Die frei wählbaren Parameter a und b werden festgelegt durch die Anfangsbedingungen
x(0) = x0, ˙x(0) = v0, (497)
mit gewissen Werten x0 und v0 für Position bzw. Geschwindigkeit zur Zeit t = 0.
geht die Einschwingphase zu Ende und es gilt
Für t ≫ 1
λ
x(t) → R cos(Ωt − Φ) (t ≫ 1/λ). (498)
82