Teil 7: Bäume Beispiele (1)
Teil 7: Bäume Beispiele (1)
Teil 7: Bäume Beispiele (1)
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
<strong>Teil</strong> 7:<br />
<strong>Bäume</strong><br />
•! <strong>Beispiele</strong><br />
•! Definition und Eigenschaften<br />
•! Implementierungen<br />
•! Durchlaufen von <strong>Bäume</strong>n<br />
•! Binäre Suchbäume<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-1<br />
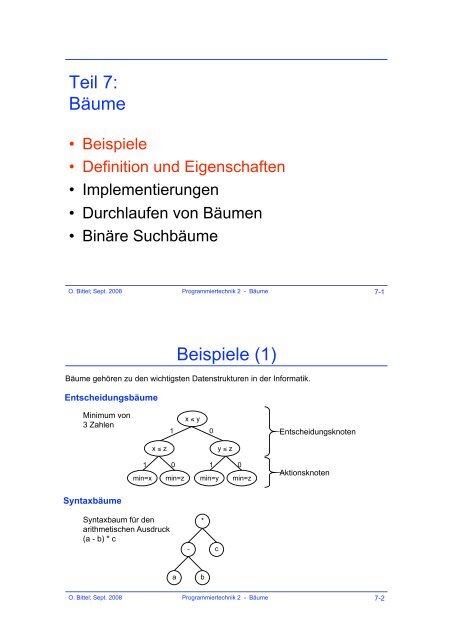
<strong>Beispiele</strong> (1)<br />
<strong>Bäume</strong> gehören zu den wichtigsten Datenstrukturen in der Informatik.<br />
Entscheidungsbäume<br />
Minimum von<br />
3 Zahlen<br />
x ! y<br />
1 0<br />
Entscheidungsknoten<br />
x ! z<br />
y ! z<br />
1 0 1 0<br />
min=x min=z min=y min=z<br />
Aktionsknoten<br />
Syntaxbäume<br />
Syntaxbaum für den<br />
arithmetischen Ausdruck<br />
(a - b) * c<br />
*<br />
- c<br />
a<br />
b<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-2
<strong>Beispiele</strong> (2)<br />
Verzeichnis-Strukturen<br />
Ausschnitt aus einer<br />
Unix-Verzeichnis-Struktur<br />
/<br />
Wurzelverzeichnis<br />
bin<br />
etc<br />
usr<br />
dev<br />
ls date who passwd src bin tty00 tty01<br />
date.c<br />
who.c<br />
Verzeichnisknoten<br />
Dateiknoten<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-3<br />
<strong>Bäume</strong>: Definition und Begriffe (1)<br />
<strong>Bäume</strong> lassen sich am einfachsten rekursiv definieren:<br />
(1)! Ein einzelner Knoten<br />
ist ein Baum.<br />
(2)! Falls B 1 , B 2 , …, B n (n " 1) <strong>Bäume</strong> sind, dann ist auch<br />
B 1 B 2<br />
B n<br />
Wurzel<br />
<strong>Teil</strong>bäume<br />
ein Baum.<br />
Hier hängen n <strong>Bäume</strong> an einem Knoten, der auch Wurzel genannt wird.<br />
Die Verbindungslinien heißen Kanten.<br />
Die <strong>Bäume</strong> B 1 , B 2 , …, B n werden auch <strong>Teil</strong>bäume genannt.<br />
(In der Informatik wachsen also <strong>Bäume</strong> in anderer Richtung als in der Natur!)<br />
(3)! Außerdem wollen wir auch die leere Menge als Baum (leerer Baum) definieren.<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-4
<strong>Bäume</strong>: Definition und Begriffe (2)<br />
Beispiel:<br />
Dieser Baum entsteht durch<br />
•! mehrmaliges Anwenden der Regel (1) und<br />
•! 2-maliges Anwenden der Regel (2)<br />
Weitere Begriffe:<br />
•!<br />
•!<br />
•!<br />
•!<br />
Die Knoten unterhalb eines Knoten k werden auch<br />
Kindknoten und k Elternknoten genannt.<br />
Knoten ohne Kinder werden Blätter genannt.<br />
Ein Baum heißt geordnet, falls die Reihenfolge der<br />
Kinder eine Rolle spielt<br />
(s. Bsp. Syntaxbaum für arithm. Ausdruck)<br />
Üblicherweise enthalten die Knoten Daten.<br />
Man spricht dann von einem markierten Baum.<br />
…<br />
…<br />
Elternknoten<br />
Kindknoten<br />
Blätter<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-5<br />
<strong>Bäume</strong>: Definition und Begriffe (3)<br />
Weitere Begriffe:<br />
•!<br />
Die Tiefe eines Knotens ist sein Abstand zur Wurzel,<br />
d.h. die Anzahl der Kanten von der Wurzel zu dem Knoten.<br />
•!<br />
•!<br />
Die Menge aller Knoten der Tiefe i wird auch i-te Ebene<br />
(level) genannt.<br />
Die Höhe eines Baums ist die maximale Tiefe,<br />
die von einem Knoten erreicht werden kann.<br />
Beispiel<br />
Ein Baum der<br />
Höhe 2.<br />
Ebene 0<br />
Ebene 1<br />
Ebene 2<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-6
Definition<br />
Binärbäume<br />
Ein Binärbaum ist ein geordneter Baum, bei dem jeder Knoten maximal 2 Kinder hat.<br />
Die beiden Kinder werden linkes und rechtes Kind genannt.<br />
Hat ein Knoten nur ein Kind, dann muss es entweder ein linkes oder ein rechtes Kind sein.<br />
<strong>Beispiele</strong><br />
a<br />
b<br />
B 1 B 2<br />
B 3<br />
<strong>Bäume</strong> B 2 und B 3 sind strukturell unterschiedlich:<br />
in B 2 hat Knoten a einen linken Sohn während in<br />
B 3 Knoten b nur einen rechten Sohn hat.<br />
B 4<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-7<br />
Definition<br />
Vollständige Binärbäume<br />
Ein vollständiger Binärbaum ist ein Binärbaum, bei der jeder Ebene (bis auf die letzte)<br />
vollständig gefüllt und die letzte Ebene von links nach rechts gefüllt ist.<br />
<strong>Beispiele</strong><br />
Ebene 0<br />
Ebene 1<br />
Eigenschaften:<br />
•!<br />
B 1<br />
Ein vollständiger Binärbaum der Höhe h mit vollständig gefüllter letzter Ebene hat<br />
n = 2 0 + 2 1 + … + 2 h = 2 h+1 – 1<br />
viele Knoten (vergleiche Baum B 3 ). Damit gilt auch<br />
h = log 2 (n+1)-1 = #log 2 n$ (abgerundet!)<br />
B 2<br />
B 3<br />
Ebene 2<br />
Ebene 3<br />
•!<br />
Ein beliebiger vollständiger Binärbaum mit n Knoten (vergleiche Baum B 2 ) hat die Höhe<br />
h = #log 2 n$<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-8
<strong>Teil</strong> 7:<br />
<strong>Bäume</strong><br />
•! <strong>Beispiele</strong><br />
•! Definition und Eigenschaften<br />
•! Implementierungen<br />
•! Durchlaufen von <strong>Bäume</strong>n<br />
•! Binäre Suchbäume<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-9<br />
Implementierung von Binärbäumen<br />
Implementierung mit verketteten Knoten<br />
Jeder Knoten hat jeweils einen Zeiger<br />
für das linke bzw. rechte Kind.<br />
root<br />
A<br />
A<br />
B<br />
C<br />
B<br />
C<br />
D<br />
E<br />
F<br />
D E F<br />
G<br />
H<br />
I<br />
G<br />
H<br />
I<br />
struct Node<br />
{<br />
int data;<br />
Node* left; // linkes Kind<br />
Node* right; // rechtes Kind<br />
};<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-10
Implementierung von beliebigen <strong>Bäume</strong>n<br />
Implementierung mit verketteten Knoten<br />
Jeder Knoten enthält 2 Zeiger:<br />
•! Ein Zeiger auf das erste Kind<br />
•! Ein Zeiger für den rechts liegenden<br />
Geschwisterknoten (engl. sibling)<br />
root<br />
A<br />
A<br />
B<br />
C<br />
D<br />
E<br />
F<br />
G<br />
B<br />
C<br />
D E F G<br />
H I J K<br />
H<br />
I<br />
J<br />
K<br />
L<br />
M<br />
L<br />
M<br />
struct Node<br />
{<br />
int data;<br />
Node* firstChild;<br />
Node* nextSibling;<br />
};<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-11<br />
Implementierung von vollständigen Binärbäumen<br />
Implementierung mit einem Feld<br />
Die Knoten werden ebenenweise in einem Feld abgespeichert.<br />
Ebene 0<br />
Ebene 1<br />
5<br />
8 7<br />
a [0] [1] [2] [3] [4] [5] [6] [7] [8] [9]<br />
5 8 7 1 3 9 2 12 10 6<br />
Ebene 2<br />
1 3 9 2<br />
Ebene 3<br />
12 10 6<br />
Effizienter Zugriff auf Eltern und Kinder:<br />
•! Kinder von a[i]: a[2*i+1] und a[2*i+2] für i " 0<br />
•! Elternknoten von a[i]: a[(i-1)/2] für i " 1 und mit ganzzahliger Division<br />
Beispiel:<br />
•! Kinder von a[3] = 1: a[7] = 12 und a[8] = 10<br />
•! Elternknoten von a[6] = 2: a[(6-1)/2] = a[2] = 7<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-12
<strong>Teil</strong> 7:<br />
<strong>Bäume</strong><br />
•! <strong>Beispiele</strong><br />
•! Definition und Eigenschaften<br />
•! Implementierungen<br />
•! Durchlaufen von <strong>Bäume</strong>n<br />
•! Binäre Suchbäume<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-13<br />
Ziel<br />
Überblick<br />
Das Besuchen aller Knoten in einer bestimmten Reihenfolge<br />
ist eine oft benötigte Operation.<br />
Durchlaufreihenfolgen<br />
•! PreOrder: besuche Wurzel, besuche linken <strong>Teil</strong>baum; besuche rechten <strong>Teil</strong>baum;<br />
•! PostOrder: besuche linken <strong>Teil</strong>baum; besuche rechten <strong>Teil</strong>baum; besuche Wurzel;<br />
•! InOrder: besuche linken <strong>Teil</strong>baum; besuche Wurzel; besuche rechten <strong>Teil</strong>baum;<br />
•! LevelOrder: besuche Knoten ebenenweise<br />
Bemerkungen<br />
•!<br />
•!<br />
Die Präfixe Pre, Post bzw. In bedeuten vorher, nachher und dazwischen.<br />
Gemeint ist damit der Zeitpunkt, an dem die Wurzel besucht wird.<br />
Um die Darstellung zu vereinfachen, werden wir die Durchlaufalgorithmen nur für<br />
Binärbäume behandeln.<br />
Die Algorithmen lassen sich in einfacher Weise auf allgemeine <strong>Bäume</strong> übertragen.<br />
Der InOrder-Durchlauf ist jedoch nur für Binärbäume sinnvoll.<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-14
PreOrder-Durchlauf für Binärbäume<br />
Algorithmus<br />
void preOrder(Node* p)<br />
{<br />
if (p != 0)<br />
{<br />
bearbeite(p->data);<br />
preOrder(p->left);<br />
preOrder(p->right);<br />
}<br />
}<br />
Beispiel<br />
*<br />
- c<br />
// Definition eines Baums:<br />
struct Node<br />
{<br />
int data;<br />
Node* left; // linkes Kind<br />
Node* right; // rechtes Kind<br />
};<br />
Node* root;<br />
…<br />
// Aufruf von preorder<br />
preOrder(root);<br />
Durchlaufreihenfolge:<br />
* - a b c<br />
a<br />
b<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-15<br />
PostOrder-Durchlauf für Binärbäume<br />
Algorithmus<br />
void postOrder(Node* p)<br />
{<br />
if (p != 0)<br />
{<br />
postOrder(p->left);<br />
postOrder(p->right);<br />
bearbeite(p->data);<br />
}<br />
}<br />
Beispiel<br />
*<br />
- c<br />
Durchlaufreihenfolge:<br />
a b – c *<br />
(Entspricht der sog. Postfix-Notation für<br />
arithmetische Ausdrücke)<br />
a<br />
b<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-16
InOrder-Durchlauf für Binärbäume<br />
Algorithmus<br />
void inOrder(Node* p)<br />
{<br />
if (p != 0)<br />
{<br />
inOrder(p->left);<br />
bearbeite(p->data);<br />
inOrder(p->right);<br />
}<br />
}<br />
Beispiel<br />
*<br />
- c<br />
Durchlaufreihenfolge:<br />
a – b * c<br />
a<br />
b<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-17<br />
LevelOrder-Durchlauf für Binärbäume<br />
Algorithmus<br />
Die Knoten werden ebenenweise in einer Schlange (Queue) gespeichert<br />
und in einer while-Schleife abgearbeitet.<br />
void levelOrder(Node* p)<br />
{<br />
Queue queue;<br />
queue.push(p); // Ebene 0<br />
}<br />
while ( !queue.empty() )<br />
{<br />
Node* q;<br />
// Schreibe vorderstes Element aus Schlange<br />
// nach q und lösche Element aus Schlange:<br />
queue.front(q);<br />
queue.remove();<br />
if (q != 0)<br />
{<br />
bearbeite(q->data);<br />
queue.push(q->left);<br />
queue.push(q->right);<br />
}<br />
}<br />
Beispiel<br />
*<br />
- c<br />
a b<br />
Durchlaufreihenfolge:<br />
* – c a b<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-18
Aufgabe 7.1<br />
Aufgaben<br />
Beschreiben Sie anhand eines Beispiels, wie Sie Verzeichnisstrukturen textuell ausgeben<br />
würden. Welche Durchlaufreihenfolge wählen Sie dabei?<br />
Schreiben Sie einen Algorithmus, um Verzeichnisstrukturen auszugeben.<br />
Aufgabe 7.2<br />
Schreiben Sie einen Algorithmus, um die Speicherplatzgröße einer gesamten<br />
Verzeichnisstruktur zu berechnen.<br />
Es kann davon ausgegangen werden, dass die Speichergröße von jedem<br />
Unterverzeichnis und jeder Datei beim entsprechenden Knoten abgespeichert ist.<br />
/<br />
bin<br />
etc<br />
usr<br />
dev<br />
ls date who passwd src bin tty00 tty01<br />
date.c<br />
who.c<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-19<br />
<strong>Teil</strong> 7:<br />
<strong>Bäume</strong><br />
•! <strong>Beispiele</strong><br />
•! Definition und Eigenschaften<br />
•! Implementierungen<br />
•! Durchlaufen von <strong>Bäume</strong>n<br />
•! Binäre Suchbäume<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-20
Knoten<br />
Definition von binären Suchbäumen<br />
Alle Knoten in einem Baum enthalten<br />
einen Schlüssel (Key) und evtl. weitere Daten (Value).<br />
Definition<br />
Ein binärer Suchbaum ist ein Binärbaum, bei dem<br />
für alle Knoten k folgende Eigenschaften gelten:<br />
struct Node<br />
{<br />
KeyType key;<br />
ValueType value;<br />
Node* left; // linkes Kind<br />
Node* right; // rechtes Kind<br />
};<br />
(1)! Alle Schlüssel im linken <strong>Teil</strong>baum sind kleiner als der Schlüssel im Knoten k<br />
(2)! Alle Schlüssel im rechten <strong>Teil</strong>baum sind größer als der Schlüssel im Knoten k<br />
Beachte: Die Schlüssel müssen hier eindeutig sein. Es ist aber auch möglich, dass gleiche<br />
Schlüssel mehrfach vorkommen dürfen, was kleine Änderungen in den Algorithmen erfordert.<br />
<strong>Beispiele</strong><br />
7<br />
2 8<br />
6<br />
2 8<br />
1<br />
3<br />
Degenerierter<br />
Suchbaum<br />
1 4<br />
4<br />
4<br />
3 6<br />
3<br />
In den <strong>Bäume</strong>n sind nur<br />
die Schlüssel dargestellt.<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-21<br />
7<br />
Suchen in binären Suchbäumen<br />
Operation searchR<br />
bool searchR(KeyType k, ValueType& v, const Node* p);<br />
Suche nach einem Knoten mit Schlüssel k im <strong>Teil</strong>baum p.<br />
Falls gefunden, wird der im Knoten abspeicherte Datenwert v und<br />
der Rückgabewert true zurückgeliefert.<br />
Falls nicht gefunden, wird der Rückgabewert false zurückgeliefert.<br />
Algorithmus<br />
Beispiel<br />
bool searchR(KeyType k, ValueType& v, const Node* p)<br />
{<br />
p 7<br />
if (p == 0)<br />
R steht für<br />
return false;<br />
rekursiv<br />
else if (k < p->key)<br />
2 8<br />
return searchR(k, v, p->left);<br />
else if (k > p->key)<br />
return searchR(k, v, p->right);<br />
else // k gefunden<br />
{<br />
1 4<br />
v = p->value;<br />
return true;<br />
3 6<br />
}<br />
} searchR(3,v,p)<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-22
Idee<br />
Einfügen in binären Suchbäumen (1)<br />
Um einen Schlüssel k einzufügen, wird zunächst nach dem Schlüssel k gesucht.<br />
Falls der einzufügende Schlüssel k nicht bereits im Baum vorkommt, endet die Suche<br />
erfolglos bei einem 0-Zeiger.<br />
An dieser Stelle wird dann ein neuen Knoten mit Schlüssel k eingefügt.<br />
Beispiel 1: füge 6 ein<br />
Beispiel 2: füge 8 ein<br />
7<br />
7<br />
7<br />
7<br />
2 9<br />
2<br />
9<br />
2<br />
9<br />
2<br />
9<br />
1 4<br />
1<br />
4<br />
1<br />
4<br />
1<br />
4<br />
8<br />
3<br />
3<br />
6<br />
3<br />
6<br />
3<br />
6<br />
Suche von 6 endet<br />
bei 0-Zeiger<br />
Ersetzte 0-Zeiger durch<br />
Zeiger auf Knoten 6<br />
Suche von 8 endet<br />
bei 0-Zeiger<br />
Ersetzte 0-Zeiger durch<br />
Zeiger auf Knoten 8<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-23<br />
Einfügen in binären Suchbäumen (2)<br />
Operation insertR<br />
bool insertR(KeyType k, ValueType v, Node*& p);<br />
Fügt im <strong>Teil</strong>baum p neuen Knoten mit Schlüssel k und Datenwert v ein.<br />
Falls Schlüssel schon vorhanden, wird kein neuer Knoten eingefügt.<br />
Beachte:<br />
Der Parameter p ist ein Ein/Ausgabeparameter und daher als Referenzparameter<br />
realisiert. Der <strong>Teil</strong>baum wird gelesen und geändert.<br />
Algorithmus<br />
bool insertR(KeyType k, ValueType v, Node*& p)<br />
{<br />
if (p == 0) {<br />
p = new Node;<br />
p->key = k; p->value = v;<br />
return true;<br />
}<br />
else if (k < p->key)<br />
return insertR(k,v,p->left);<br />
else if (k > p->key)<br />
return insertR(k,v,p->right);<br />
else // k bereits vorhanden<br />
return false;<br />
}<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-24<br />
p<br />
3<br />
7<br />
2 9<br />
1 4<br />
p<br />
1<br />
insert(6, v, p)<br />
2<br />
3<br />
7<br />
4<br />
9<br />
6
Löschen in binären Suchbäumen (1)<br />
Idee<br />
Um einen Schlüssel k zu löschen, wird zunächst nach dem Schlüssel k gesucht.<br />
Es sind dann 4 Fälle zu unterscheiden:<br />
Fall „Nicht vorhanden“:<br />
Schlüssel k kommt nicht vor:<br />
dann ist nichts zu tun.<br />
Fall „Keine Kinder“:<br />
Der Schlüssel kommt in einem Blatt vor (keine Kinder):<br />
dann kann der Knoten einfach entfernt werden.<br />
Fall „Ein Kind“:<br />
Der Knoten mit dem gefundenen Schlüssel hat genau ein Kind:<br />
s. nächste Folie<br />
Fall „Zwei Kinder“:<br />
Der Knoten mit dem gefunden Schlüssel hat zwei Kinder<br />
s. übernächste Folie<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-25<br />
Löschen in binären Suchbäumen (2)<br />
Fall „Ein Kind“<br />
Der zu löschende Knoten k hat genau ein Kind.<br />
Überbrücke den Knoten k, indem der Elternknoten von k auf Kind von k verzeigert wird<br />
(Bypass) und lösche k.<br />
Beispiel: lösche Knoten mit Schlüssel 4<br />
7<br />
7<br />
7<br />
2<br />
9<br />
2<br />
9<br />
2<br />
9<br />
1<br />
4<br />
1<br />
4<br />
1<br />
3<br />
3<br />
3<br />
Suche 4<br />
Knoten 4 wird<br />
überbrückt (Bypass)<br />
Knoten 4 wird<br />
gelöscht<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-26
Löschen in binären Suchbäumen (3)<br />
Fall „Zwei Kinder“ :<br />
Der zu löschende Knoten k hat zwei Kinder.<br />
1. Ersetze den Knoten k durch den kleinsten Knoten k min im rechten <strong>Teil</strong>baum von k.<br />
2. Lösche dann k min . Da der kleinste Knoten k min im linken <strong>Teil</strong>baum kein linkes Kind hat,<br />
kann das Löschen von k min wie im Fall „Ein Kind“ bzw. „Keine Kinder“ behandelt werden.<br />
Beispiel: lösche Knoten mit Schlüssel 2<br />
7<br />
7<br />
7<br />
7<br />
2<br />
9<br />
2<br />
9<br />
3<br />
9<br />
3<br />
9<br />
1<br />
5<br />
1<br />
5<br />
1<br />
5<br />
1<br />
5<br />
3<br />
6<br />
3<br />
6<br />
3<br />
6<br />
6<br />
4<br />
4<br />
4<br />
4<br />
Suche 2<br />
Suche kleinsten Knoten in<br />
rechten <strong>Teil</strong>baum von 2<br />
Knoten 2 wird durch<br />
kleinsten Knoten ersetzt<br />
kleinster Knoten<br />
wird gelöscht<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-27<br />
Löschen in binären Suchbäumen (4)<br />
bool removeR(KeyType k, Node*& p)<br />
{<br />
if (p == 0) // k nicht vorhanden<br />
return false;<br />
else if (k < p->key)<br />
return removeR(k,p->left);<br />
else if (k > p->key)<br />
return removeR(k,p->right);<br />
else if (p->left == 0 || p->right == 0) {<br />
Node* temp = p;<br />
if (p->left != 0)<br />
}<br />
p = p->left; // Bypass zu linkes Kind<br />
else<br />
p = p->right; // Bypass zu rechtes Kind<br />
delete temp;<br />
return true;<br />
}<br />
else {<br />
// Min. im rechten <strong>Teil</strong>baum suchen:<br />
Node* min = searchMinR (p->right);<br />
// Zu löschender Knoten durch Min. ersetzen<br />
p->data = min->data; p->key = min->key;<br />
// Min. in rechtem <strong>Teil</strong>baum löschen:<br />
return removeR (min->key, p->right);<br />
}<br />
Operation removeR<br />
Löscht im <strong>Teil</strong>baum p Knoten mit Schlüssel k.<br />
Der Parameter p ist ein Ein/Ausgabeparameter<br />
und daher ein Referenzparameter.<br />
Knoten hat ein Kind<br />
oder kein Kind<br />
Knoten hat<br />
zwei Kinder<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-28
Löschen in binären Suchbäumen (5)<br />
Operation searchMinR<br />
Sucht im <strong>Teil</strong>baum p nach dem kleinsten Knoten und<br />
liefert Zeiger auf Minimum zurück.<br />
Node* searchMinR(const Node* p)<br />
{<br />
if (p == 0) // Minimum nicht vorhanden<br />
return 0;<br />
else if (p->left == 0) // Minimum gefunden<br />
return p;<br />
else<br />
return searchMinR (p->left);<br />
}<br />
Bemerkung<br />
Beachten Sie, dass in der Operation removeR im Fall „Knoten hat zwei Kinder“ der<br />
Aufruf von searchMinR und der rekursive Aufruf von removeR bedeuten, dass zweimal<br />
vom rechten Kind p->right zum kleinsten Knoten gelaufen wird.<br />
Diese Ineffezienz lässt sich jedoch beheben, indem searchMinR noch zusätzlich das<br />
Löschen des kleinsten Elements übernimmt. Der rekursive Aufruf von removeR ist dann<br />
überflüssig.<br />
Diese Variante findet sich in der Quell-Code-Sammlung zur Vorlesung.<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-29<br />
Worst-Case<br />
Analyse<br />
Da im schlechtesten Fall ein binärer Suchbaum mit n Knoten zu einem Baum der Höhe<br />
n-1 entarten kann (Bsp?), haben die Operationen zum Suchen, Einfügen und Löschen<br />
eine maximale Suchlänge von n.<br />
Damit: T max (n) = O(n)<br />
Average-Case<br />
In [Ottmann und Widmayer 2002] wird gezeigt, dass die durchschnittliche Laufzeit um<br />
eine Größenordnung besser ist. Es werden zwei Ergebnisse hergeleitet, die sich darin<br />
unterscheiden, welche Verteilung der <strong>Bäume</strong> angenommen wird:<br />
•!<br />
<strong>Bäume</strong> mit n Knoten entstehen durch eine Folge von Einfüge-Operationen von n<br />
unterschiedlichen Elementen. Es wird angenommen, dass jede der n! möglichen<br />
Anordnungen der Elemente gleichwahrscheinlich ist. Gemittelt wird dann über die n!<br />
viele auf diese Weise erzeugten <strong>Bäume</strong>. Man erhält dann für die Such-Operation eine<br />
mittlere Suchlänge von ungefähr 1.4 log 2 n.<br />
Damit: T mit (n) = O(log 2 n)<br />
•!<br />
Es wird angenommen, dass alle strukturell verschiedenen binären Suchbäume mit n<br />
Knoten gleichwahrscheinlich sind. Man erhält dann für die Such-Operation eine<br />
mittlere Suchlänge von ungefähr<br />
Damit: T mit (n) = O( )<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-30
Aufgabe 7.3<br />
Aufgabe 7.4<br />
Aufgaben (1)<br />
Geben Sie den binären Suchbaum an, nachdem mit einem leeren Baum<br />
begonnen wurde und folgende Operationen durchgeführt worden sind:<br />
•! Einfügen von: 10, 5, 3, 8, 2, 4, 1, 15, 12, 17, 6, 7, 9<br />
•! Löschen von: 2, 3, 5, 12, 10<br />
Beseitigen Sie die beiden endrekursiven Aufrufe in der Funktion searchR.<br />
Aufgabe 7.5<br />
Schreiben Sie eine Funktion, die das größte Element in einem binären Suchbaum<br />
findet und zurückliefert.<br />
Aufgabe 7.6<br />
Schreiben Sie eine Funktion makeEmpty, die den Speicherplatz für einen binären<br />
Suchbaum vollständig freigibt.<br />
Aufgabe 7.7<br />
Schreiben Sie eine Funktion copy, die eine Kopie eines binären Suchbaums erstellt und<br />
zurückliefert.<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-31<br />
Aufgabe 7.8<br />
Aufgaben (2)<br />
Schreiben Sie eine Funktion save, die einen binären Suchbaum auf eine Datei schreibt<br />
und eine Funktion read, die einen binären Suchbaum von einer Datei einliest.<br />
Es sind 2 Varianten vorzusehen:<br />
a)! Die Funktionen save und read sollen strukturerhaltend sein. D.h. nach<br />
Abspeichern und wieder Einlesen hat der binäre Suchbaum die gleiche Struktur<br />
wie zuvor.<br />
b)! Die Funktionen save und read müssen nicht strukturerhaltend sein. Vielmehr<br />
wird gefordert, dass beim Einlesen ein binärer Suchbaum mit minimaler Höhe<br />
erzeugt wird.<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-32
Klasse BinarySearchTree<br />
Ziel<br />
Klasse BinarySearchTree, mit der sich eine Menge von Elementen,<br />
bestehend aus Schlüssel und Wert effizient verwalten lassen.<br />
Implementierung als binärer Suchbaum.<br />
Beispiel: Telefonbucheintrag mit Schlüssel = Name und Werte = Telefonnummer.<br />
Schnittstelle<br />
•! search(k, v) Sucht nach Schlüssel k und liefert zugehörigen Wert v<br />
(Ausgabeparameter) zurück<br />
•! insert(k,v) Fügt neues Element mit Schlüssel k und Wert v ein<br />
•! remove(k) Löscht Element mit Schlüssel k<br />
Flexibilität durch Schablonenmechanismus<br />
Der Schlüsseltyp und der Typ der Elementwerte sind parametrisiert.<br />
Damit lassen sich verschiedene Anwendungen einfach realisieren.<br />
<strong>Beispiele</strong>:<br />
// Telefonbuch:<br />
typedef string FamName;<br />
typedef string TelNr;<br />
Schlüssel-Typ<br />
Elementwerte-Typ<br />
// Wörterbuch:<br />
typedef string Deutsch;<br />
typedef string Englisch;<br />
BinarySearchTree < FamName, TelNr> telBuch;<br />
BinarySearchTree wBuch;<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-33<br />
Öffentlicher <strong>Teil</strong> der Klasse BinärySearchTree<br />
template <br />
// KeyType erfordert Vergleichsoperatoren . ValueType erfordert Zuweisungsoperator =<br />
class BinarySearchTree<br />
{<br />
Schlüssel-Typ<br />
public:<br />
BinarySearchTree() {root = 0;}<br />
Elementwerte-Typ<br />
~BinarySearchTree() {makeEmptyR(root);}<br />
void traverse() const { traverseR(root);}<br />
// Travesiert über alle Schlüssel in sortierter Reihenfolge und gibt Daten aus.<br />
bool search(const KeyType& k, ValueType& v) const { return searchR(k,v,root);}<br />
// Sucht Schlüssel k und liefert Wert v falls gefunden.<br />
// Gibt true zurück, falls Schlüssel k gefunden wird, und sonst false.<br />
bool insert(const KeyType& k, const ValueType& v) { return insertR(k,v,root);}<br />
// Fügt neuen Schlüssel k mit Wert v ein. Falls Schlüssel bereits vorhanden ist,<br />
// wird nicht eingefügt und false zurückgeliefert, sonst true.<br />
bool remove(const KeyType& k) { return removeR(k,root);}<br />
// Löscht Schlüssel k. Falls Schlüssel gelöscht werden konnte wird true zurückgeliefert<br />
// und sonst false (d.h. Schlüssel war nicht vorhanden).<br />
private:<br />
// …<br />
};<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-34
Privater <strong>Teil</strong> der Klasse BinärySearchTree<br />
template <br />
class BinarySearchTree<br />
{<br />
public:<br />
// …<br />
private:<br />
struct Node<br />
{<br />
KeyType key;<br />
Deklaration eines<br />
ValueType value;<br />
Binärbaums<br />
Node* left;<br />
Node* right;<br />
// Konstruktor<br />
Node(const KeyType& k, const ValueType& v) : key(k), value(v), left(0), right(0) {}<br />
};<br />
Node* root;<br />
};<br />
void traverseR(const Node* p) const;<br />
bool searchR(const KeyType& k, ValueType& v, const Node* p) const;<br />
bool insertR(const KeyType& k, const ValueType& v, Node*& p);<br />
bool removeR(const KeyType& k, Node*& p);<br />
Rekursive, private<br />
Methoden<br />
void getRemoveMin(KeyType& k, ValueType& v, Node*& p); // Hilfsmethode für removeR<br />
void makeEmptyR(Node* p);<br />
O. Bittel; Sept. 2008 Programmiertechnik 2 - <strong>Bäume</strong> 7-35