TM1 Seilstatik - Institut für Angewandte und Experimentelle Mechanik

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 1
7.2 Anwendung auf typische Belastungsfälle
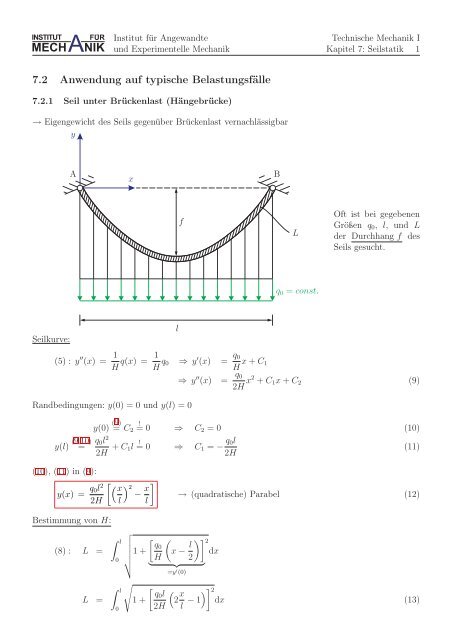
7.2.1 Seil unter Brückenlast (Hängebrücke)
→ Eigengewicht des Seils gegenüber Brückenlast vernachlässigbar
y
A
x
B
f
L
Oft ist bei gegebenen
Größen q 0 , l, und L
der Durchhang f des
Seils gesucht.
q 0 = const.
Seilkurve:
l
(5) : y ′′ (x) = 1 H q(x) = 1 H q 0 ⇒ y ′ (x) = q 0
H x + C 1
Randbedingungen: y(0) = 0 und y(l) = 0
⇒ y ′′ (x) = q 0
2H x2 + C 1 x + C 2 (9)
y(0) (9) !
= C 2 = 0 ⇒ C 2 = 0 (10)
y(l) (9,10) = q 0l 2
2H + C 1l = ! 0 ⇒ C 1 = − q 0l
(11)
2H
(10), (11) in (9):
y(x) = q [
0l 2 (x
2H l
) ] 2 x −
l
→ (quadratische) Parabel (12)
Bestimmung von H:
(8) : L =
L =
∫ l
0
∫ l
0
[ (
√ 1 + q0
x − l )] 2
dx
H 2
} {{ }
=y ′ (0)
√
[
q0 l
1 +
(2 x ) ] 2
2H l − 1 dx (13)

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 2
Substitution:
q 0 l
(2 x )
2H l − 1
= sinhu
Lösung:
L = H 2q 0
[u + sinh(u) cosh(u)] u(x=l)
u(x=0)
(14)
→ Transzendente Gleichung, aus der H bei gegebenem L numerisch ermittelt werden kann.
Analytische Näherungslösung:
Annahme = „flach gespanntes Seil“ mit |y ′ | ≪ 1
Mit der Reihenentwicklung
hier: |y ′ | max = |y ′ (0)| = |y ′ (l)| = q 0l
2H ≪ 1
√
1 + u = 1 +
1
2 u − 1 8 u2 + 1 16 u3 − ... ≈ 1 + 1 2 u
folgt aus (13) näherungsweise
L =
=
=
∫ l
0
∫ l
0
1 + 1 2
[
q0 l
(2 x ) ] 2
2H l − 1 dx
1 + q 0 2 l 2
8H 2 (
4 x2
l 2 − 4x l + 1 )
dx
[x + q 0 2 l 2
8H 2 ( 4
3
)]
x 3
l − 3 2x2 + x
l
L = l + q 0 2 l 3 ( 4
8H 2 3 − 2 + 1
) q 2 0 l 3
= l +
} {{ } 24H 2
= 1 3
0
l
H 2 = q 0 2 l 2
24
l
L − l
⇒
H = q 0l
2 √ 6
1
√
L
− 1
l
(15)
(15) in (12) ergbit die Seilkurve für ein flach gespanntes Seil unter Brückenlast:
y(x) = √ [ (x ) 2 ( x
) ]
6l(L − l) − (16)
l l
Berechnung des Durchhangs f:
Aus der Symmetrie des vorliegenden Problems ist sofort ersichtlich, dass die maximale Auslenkung
des Seils bei x = a = l 2 auftritt. Ansonsten ist a aus der Bedingung y′ (a) = 0 zu bestimmen.
• Für Seilkurve ohne Näherung:
( l (12)
f = −y = −
2)
q (
0l 2 1
2H 4 2)
− 1
= q 0l 2
8H
mit H aus (14) (17)

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 3
• Für straff gespanntes Seil (Näherung):
( l (16)
f = −y = −
2)
√ ( 1
6l(L − l)
4 2)
− 1
√
3
= (L − l)l (18)
8
Zahlenbeispiel: l = 100m, L = 102m ⇒ f (18) = √ 75m ≈ 8, 66m
Zusatz: Seikraft
(6) → S(x) = H √ 1 + y ′2 (x)
• Für flach gespanntes Seil unter Brückenlast (Näherung):
(16) → y ′ (x) =
⇒ S(x)
(15)
=
S(x) = q 0l
2
√
6(L − l)
(2 x )
l l − 1 √ √
q 0 l l
2 √ 6(L − l)
1 +
(2 x ) 2
6 L − l l l − 1 √
l
(
6(L − l) + 2 x ) 2
l − 1 (19)
Die Seilkraft wir maximal an den Lagerungen, d.h. bei x = 0 und x = l.
√
S(0) = q 0l l
1 + = S(l) (19a)
2 6(L − l)
Zahlenbeispiel von oben: S(0) ≈ 1, 53q 0 l = 1, 53G Brücke
Bemerkung:
Aus (6) ist sofort ersichtlich, dass S(x) minimal ist für x = a = l , wo 2 y′ (a) = y ( ′ l
2)
= 0 gilt.
( l
S(a) = S = H , d.h. and der „Durchhangstelle“ ist die Seilkraft nur gleich dem Horizontalzug H.
2)
7.2.2 Seil unter Eigengewicht (Kettenlinie)
Streckenlast = Eigengewicht des Seils (homogen)
gleichmäßig verteilt über der (Bogen-) Längskoordinate s des Seils
⇒ q(s) = q 0 = γ = ρg ; 0 ≤ s ≤ L

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 4
ds
q(s) = γ
dy
Es gilt, dass die Vertikalkräfte gleich sein müssen:
⇒ γds = q(x)dx (20)
Außerdem gilt:
ds 2 = dx 2 + dy 2 (21)
aus (20) und (21):
q(x)
√
q(x) = γ ds ( ) 2 dy
dx = γ 1 + = γ√
1 + y
dx
′ 2
(22)
dx
Einsetzen in die Differenatialgleichung der Seilkurve (5) ergibt:
y ′′ (x) = γ H
√
1 + y ′ 2 (x) (nichtlineare) DGL der Kettenlinie (23)
Lösung der (nichtlinearen) Differentialgleichung (23):
• Substitution: y ′ = u ;
• Trennung der Variablen
• Integration
y ′′ = u ′ = du
dx
∫ u
ũ=u 0
dũ
√
1 + ũ
2
du
dx =
= γ H
γ √
1 + u
2
H
∫ x
˜x=x 0
d˜x
arsinh(ũ)| u u 0
= γ H (x − x 0)
arsinh(u) = γ H (x − x 0) + arsinh(u 0 )
u = y ′ = dy ( γ
)
dx = sinh H (x − x 0) + arsinh(y 0)
′
∫ y
y 0
dỹ =
∫ x
x 0
sinh
( γ
H (x − x 0) + arsinh(y ′ 0))
d˜x
y(x) = y 0 + H [ ( γ cosh
γ H (x − x 0) + arsinh(y 0))
′ − cosh (arsinh(y 0))
′
√
} {{ }
=
1+y ′ 02 aus: cosh 2 z−sinh 2 z =1
]
(24)

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 5
Wahl eines speziellen Koordinatensystems (Ursprungslage):
y
B
f
A
H
γ
x
x 0 = 0
y 0 = H γ
y 0 ′ = 0
⇒
y(x) = H γ + H γ
[cosh( γ H x) − 1 ]
y(x) = H γ cosh( γ H
x) Kettenlinie = Kurve des Seils unter Eigengewicht (25)
Bestimmung von H:
∫ x B
√
aus (8): L = 1 + y
′2
(x)dx (25) =
x=x A
=
∫ x B
x A
cosh( γ H x)dx = H γ
∫ x B √
x A
1 + sinh 2 ( γ H x)dx
(
sinh( γ H x B) − sinh( γ )
H x A)
(26)
→ Transzendente Gleichung, aus der H bei gegebenem L numerisch ermittelt werden kann.
Analytische Näherungslösung:
Annahme: „straff gespanntes Seil“ (= „flach durchhängende Kette“) mit:
y ′ (x) ≪ 1 , d. h. sinh( γ H x) ≈ γ H x ≪ 1
Mit der Reihenentwicklung
cosh u = 1 + u2
2!
+ u4
4!
folgt aus (25) näherungsweise:
+ u6 u2
... ≈ 1 +
6! 2!
y(x) = H γ + γ
2H x2 Kurve des straff gespannten Seiles unter Eigengewicht (27)
→ Das straff gespannte Seil hängt unter Eigengewicht näherungsweise parabelförmig durch (vgl.
konstantes q(x) unter 7.2.1).

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 6
Mit (27) folgt aus (8), wie auch aus (26) unter Verwendung von sinh u ≈ u + u3
3!
:
L = (x B − x A ) + γ2
6H 2(x B 3 − x A 3 )
√
⇒ H = √ γ x B3 − x 3 A
6 L(x B − x A )
(28)
Berechnung des Durchhangs f (von Aufhängung A aus):
f = y(x A ) − y(0) (siehe Bild) (29)
• Für die Kettenlinie (ohne Näherung):
(25) → f = H γ
(
cosh( γ )
H x A) − 1
mit H aus (26) (30)
• Für das straff gespannte Seil (näherungsweise):
Zusatz: Seilkraft
(27) → f = γ
2H x A 2 mit H aus (28) (31)
(6): S(x) = H √ 1 + y ′2 (x)
• Für Kettenlinie:
S(x) (25) = H
√
1 + sinh 2 ( γ H x) = H cosh( γ (25)
x) = γ y(x) (32)
H
⇒ S max = γ y max ,
d.h. die größte Seilkraft tritt bei x A oder x B auf (Lager!) mit
y max = max{y A , y B }
• Für straff gespanntes Seil:
√
S(x) (27) = H 1 + γ2
= √ H
H 2 + γ 2 x 2 (28) = γ
2x2
√
x B3 − x A
3
6(L − (x B − x A )) + x2 (33)
⇒ S max tritt an den Rändern, d.h. in einem der Lager auf, also in x A oder x B .
Für ein symmetrisch aufgehängtes Seil mit
y(x A ) = y(x B ) und x B − x A = l, d.h. x A = − l und x 2 B = l , folgt aus (33):
2
√
S max = S(− l 2 ) = S( l 2 ) = γ l l
1 +
2 6(L − l)
(vgl. (18)) (34)

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 7
Beispiel: Freileitung
A
y
B
L
f
x
Geg.:
γ = 120 N m
l = 100 m
L = 110 m
l
Ges.: Durchhang f, maximale Seilkraft S max (mit Näherung)
(31) → f = γ
2H x2 A,B = γ
2H (± l 2 )2 = γl2
8H
√ √√√
(28) → H = √ γ ( l 2 )3 − (− l 3
2 )
6 L − ( l + l ) = − γl
2 2
2 √ 6
√
l
L − l
⇒ f =
√
3
l(L − l) (vgl. (18))
8
f = √ 375 m ≈ 19, 4 m
⇒ H ≈ 7746 N ≈ 7, 7 kN
√
(34) → S max = γl l
1 +
2 6(L − l)
Bemerkung:
≈ 9788 N ≈ 9, 8 kN
|y ′ max| = |y ′ (± l 2 )| ≈ γ H
l
2
≈ 0, 77
|y ′ max| ≪ 1 ist nicht sehr gut erfüllt, dennoch ist die Näherung sehr brauchbar.

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 8
Hängende Kette.
Gateway Arch, St. Louis, MO, USA.
7.2.3 Seil unter Einzelkraftbelastung
→ Einzelkräfte sind groß im Vergleich zur Gewichtskraft des Seils ⇒ q(x) ≈ 0
l
A
y
B
f
x
L
F
Durchhang: Aus der Geometrie erhält man für das undehnbare Seil
( ) 2 l
f 2 + =
2
( L
2
) 2
⇒ f = 1 2
√
L2 − l 2 (35)
Seilkurve:
(5) → Hy ′′ (x) = q(x) = 0 ⇒ y ′′ (x) = 0 ⇒ y(x) = C 1 x + C 2 (36)
Für das gewählte Koordinatensystem gilt:
(
y(0) = 0 und y − l ) ( l
= y = f (37)
2 2)
Aus (36) und (37) folgt mit (35):
y(x) =
√
L
2
− 1 |x| (38)
l2 Die Seilkurve besteht also aus zwei Geraden ( bzw. aus mehreren Geraden im Falle mehrerer Einzelkräfte)

Institut für Angewandte
und Experimentelle Mechanik
Technische Mechanik I
Kapitel 7: Seilstatik 9
Seilkraft:
l
A
B
L
2
S
α
f
S
L
2
F
Kräftegleichgewicht:
2S cos α = F
Geometrie: cos α = f L
2
⇒ S = Fl
4f
= 2f L
(39)
(39) mit (35) : S = F 2
L
√
L2 − l 2 = F 2
1
√
(40)
1 − l2
L 2
Für l → L : S → ∞
Für l = L : S = F 2
Zusatz: Für den Horizontalzug H folgt aus der Geometrie:
H = S sin α;
sin α = l L
⇒
H = S l L
(41)
⇒ H = F 2
l
√
L2 − l 2 (42)
Bemerkung: (41) folgt auch aus (5) mit y ′2 (x) = L2
l 2 − 1 aus (38).