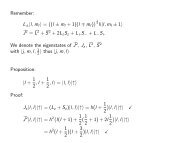C. Cohen-Tannoudji, B. Diu, F. Laloe, Quanten mechanics 1 & 2

Literatur:
C. Cohen-Tannoudji, B. Diu, F. Laloe, Quanten mechanics 1 & 2 (Wiley 1997)
R.P. Feynman, R.B. Leighton, M. Sands, The Feynman Lectures on Physics, Vol. III (Addison-Wesley, Reading, 1971)
R.P. Feynman, A.R. Hibbs, Quantum Mechanics and Path Integrals (McGraw-Hill, New York, 1965)
W. Greiner, Theoretische Physik, Quantum Mechanics (Springer 2000)
L.D. Landau, E.M. Lifschitz, Quantum Mechanics (Butterworth Heinemann, 1981)
A. Messiah, Quantum Mechanics, Vol. I, II (Dover, 2003)
L. Schiff, Quantum Mechanics (McGraw-Hill, New York, 1968)
F. Schwabl, Quantum Mechanik (Springer, 2007) *

W in eV 4.5 4.2 4.6 4.8 1.8 5.3
1.2.1.2 Photoelektrischer Effekt
Photoelectric effect
1 eV b= λ =1.24 × 10 −4 cm b= 1.6 × 10 −12 erg
4 eV b= λ =3.1 × 10 −5 cm, d. h. Ultraviolett
Hertz 1887: Electrons with maximum kinetic energy
Strahlt man Licht der Frequenz ω (im Ultravioletten, bei Alkalimetallen auch
im Sichtbaren) auf eine Metallfolie oder -oberfläche (Hertz 1887, Lenard), so
beobachtet man, daß Elektronen mit einer maximalen kinetischen Energie
von
Wir gelangen also zu folgender Hypothese: Licht besteht aus P
E e = mv2 e
der Energie = ω − W (W = Austrittsarbeit)
2
E = ω, der Geschwindigkeit work function c und einer Fortpflanzung
parallel zum elektromagnetischen Wellenvektor k (Begründung: L
mit Wellenzahl k). Damit aber lassen sich auch schon Aussagen üb
und Masse des Photons machen.
emittiert werden (Abb. 1.3). Dies führte Albert Einstein 1905 zu der Hypothese,
=⇒ daß Light: Licht Photons aus Photonen, with energy Energiequanten derE Energie = ωω, besteht.
Danach kann ein im Metall gebundenes Elektron nur dann von einem auftreffenden
Photon herausgelöst werden, wenn dessen Energie die Austrittsarbeit
We Aus know derfrom Relativitätstheorie Special Relativity (SRT) ist bekannt:
W nicht unterschreitet.
E = √ p 2 c 2 + m 2 c 4 ;
Since |v| = c =⇒ m =0=⇒ E = pc
v = ∂E
∂p = pc 2
√
p2 c 2 + m 2 c 4 .
Wegen |v| = c folgt aus (1.3) m = 0 und somit E = pc. Vergle
dies electromagnetic mit E = ω waves: = ck ω = ck (elektromagnetische =⇒ E = ω = ck = Wellen: pc =⇒ p ω = kck), er
p = k. Weil p und k parallel sind, folgt ferner p = k. Also:
in general.: E = ω , p = k
E = ω } µ
( E/c
) ( k
)

Wave Properties of Particles
Same procedure for matter (Davisson, Germer; Thomson, Rupp 1928)
Electrons possess wave properties: interference on crystal lattice
storische 8 und experimentelle 1. Historische Grundlagen
experimentelle Grundlagen
m Weg empirical sichfür auf nichtrelativistische diesem observation Weg fürfor nichtrelativistische Elektronen non-relativistic (Kinetische Elektronen electrons Energie (Kinetische (E kin = Energie
p2
): E 2m )
kin = p 2 /2m):
=
2πc
λ = 2π
p 2πc
√ 2mc2 (p 2 /2m) = √ 12.2 Å
Ekin (eV) . (1.7)
2mc2 (p 2 /2m) = √ 12.2 Å
Ekin (eV) . (1.7)
mentelle Dieser Befund experimentelle ist in genauer Befund Übereinstimmung ist genauer mit Übereinstimmung der von de mit der von de
aufgestellten Broglie exact agreement Hypothese, 1923 aufgestellten with daß einem hypothesis Hypothese, Teilchen made daß miteinem Gesamtenergie
by de Teilchen Broglie mit (1923) Gesamtenergie
ls p eine E und Frequenz Impulsω p= eine E/Frequenz und eineω Wellenlänge = E/ undλ eine =2π/p Wellenlänge λ =2π/p
st. Welche zuzuordnen physikalische ist. Welche Bedeutung physikalische diese Welle Bedeutung hat, müssen diese Welle wir hat, müssen wir
lären später (s. Abschn.
ω
noch
= E/
klären 2.1). Daß
,(s. Abschn. aber
λ =
auch 2π 2.1). im Daß mikroskopischen aber
λ
auch
= 2π imBe-
chenbegriff reich der qualitativ Teilchenbegriff seine Existenzberechtigung qualitativ p seine Existenzberechtigung hat, kannk
man hat, kann man
mikroskopischen Be-
den Phänomenen an den folgenden sehen: Phänomenen sehen:
de Broglie relations
sspuren – in Ionisationsspuren der Wilson-Kammer: in der Die Wilson-Kammer: in die mit übersättigtem Die in die mit übersättigtem
mpf gefüllte Wasserdampf Kammer eindringenden gefüllte Kammer Elektronen eindringenden ionisieren Elektronen die ionisieren die
entlangGasatome ihrer Flugbahn. entlangDiese ihrerIonen Flugbahn. wirkenDiese als Kondensatiund
führen Duality: onskeime beiparticle+wave Expansion und führen undbei properties damit Expansion Abkühlung (for undphotons damit des Wasser-
Abkühlung und electrons) des Wasser-
Ionen wirken als Kondensatiur
Bildung dampfes kleinerzur Wassertröpfchen.
Bildung kleiner Wassertröpfchen.

unktion
on2.1 Die Wellenfunktion
cheinlichkeitsinterpretation
lichkeitsinterpretation
und Wave ihre function Wahrscheinlichkeitsinterpretation
and Schrödinger equation
und ihre Wahrscheinlichkeitsinterpre
Gemäß den Überlegungen in Abschn. 1.2.2 in Zu
ngen tronenbeugung kommen einem Elektron auch W
Abschn. Gemäß wave in function, Abschn. den 1.2.2Überlegungen in interpretation
Zusammenhang Zusammenhang Abschn. mit der1.2.2 Elekeen
tronenbeugung Elektron einem Elektron auch kommen Welleneigenschaften auch Welleneigenschaften einem Elektron zu; diese auch zu; Welleneigenschaften diese
zu; dies
mit in der Zusammenhang Elek-
mit der Elek
sei ψ(x,t). Für freie8Elektronen 1. Historische mit Impuls
kann man diese in Einklang mit den Ergebnissen
Welle sei ψ(x,t).
2.1 Die
Für
Wellenfunktion
lektronen freiefree Elektronen electrons: mit Impuls mit momentum pImpuls und freieEnergie Elektronen p undE Energie = pmit Impuls p und Energie E = p 2 /2m
als freie ebene 2 /2mE = p 2 /2m
und ihre Wahrscheinlichkeitsinterpretation Welle ansetzen, sich auf d. h. diesem ψ hat die Weg For
nklang mit kann denman mit den dieseErgebnissen in Einklang des des mitBeugungsexperimentes
den Ergebnissen des Beugungsexperimente
Gemäß den Überlegungen in Abschn. 1.2.2 in Zusammenhang
als freie ebene Welle ansetzen, d. ψ(x,t)=Ce h. ψ hat die i(k Form .
mit der Elektronenbeugung
ψForm
hatplane diekommen Form wave einem Elektron auch Welleneigenschaften zu; diese mit ω = E/ , k =
x−ωt)
E kin = p 2 /2m):
ansetzen, n, d. de h. Broglie ψ hat d. h. die 1923:
Welle sei ψ(x,t). Für freie Elektronen mit Impuls p und Energie E = p
ψ(x,t)=Ce i(k . 2 /2m
kann man x−ωt) diese in Einklang mit den Ergebnissen des Beugungsexperimentes
ωt) it ω mit = E/ ω , = alsk E/ freie
=
ebene
p/ , Welle
. k ansetzen, = with mit p/ Nun d. ω h. . wollen ψ= hatE/ die(2.1)
Form wir , uns k = der p/ (2.1) Frage . zuwenden, λ = 2π welche (2.1p
ψ(x,t)=Ce se Wellenfunktion besitzt. Dazu betrachten wir e
Nun wollen wir uns der i(k . x−ωt)
p
= √ 2m
mit ω = E/ , k = p/ . (2.1)
e zuwenden, welche physikalische
er Frage zuwenden, Frage periment zuwenden, Bedeutung
( Gedankenexperiment“).
welche dieazu
betrachten wir
physikalische Bedeutung die
Nun wollen welche wir uns der physikalische Frage zuwenden, welche
se Wellenfunktion besitzt. ”
Bedeutung physikalische Bedeutung diesitzt.
Gedankenexperiment:
Dazu betrachten wir eindouble idealisiertes slit Beugungsex-
idealisiertes Dieser experimentelle
Beugungsex
diese
Wellenfunktion
ein idealisiertes
besitzt. DazuBeugungsex-
ment“).
( Gedankenexperiment“).
( ”
betrachten wir ein idealisiertes wir ein experiment“).
Broglie 1923 aufgestel
”
E und Impuls p eine
double screen
slit
zuzuordnen ist. Welch
später noch klären (s
reich der Teilchenbegr
an den folgenden Phä
intensity
– Ionisationsspuren
Wasserdampf gefü

dafür, daß das Elektron an der Stelle x auftrifft. ϱ(x,t) d 3 x ist dann die Wahr-
3
renzerscheinungen mit ganz entsprechenden Schirmbildern kennen wir bereits
aus der Optik für Licht und ebenso bei Wasserwellen. Geht von Spalt 1 eine
elektromagnetische amplification Zylinderwelle where mit path elektrischem length difference Feldvektorbetween E 1 (x,t), the von
Spalt 2 eine solche slits mit ∆l Feldvektor in an integral E 2 (x,t) multiple aus, ergibt of electron sich für wavelength:
die genannten
Versuchsanordnungen:
∆l = n · λ
Falls nur Spalt 1 geöffnet ist, hat man am Schirm die Intensitätsverteilung
therefore I 1 (x) =|E we have: 1 (x,t)| ρ(x) 2 , falls = ρnur 1 (x)+ρ Spalt 2 (x) 2 offen ist, erhält man stattdessen I 2 (x) =
|E 2 (x,t)| 2 (Hier haben wir E j (x,t) ∝ exp{−iωt} angenommen, was der
Zeitmittelung der Intensitäten von reellen Feldern bis auf einen Faktor 2
very äquivalent similar toist.) optics: Stehen beide Spalte offen, muß man die Wellen überlagern
electric
und bekommt
field E 1 ( E 2 , E ), intensity I = |E| 2
Interference:
E(x,t)=E 1 (x,t)+E 2 (x,t) ,
I = |E(x,t)| 2 = I 1 + I 2 + 2 Re(E ∗ 1 . E 2 ) .
Der dritte Summand in der Gesamtintensität stellt den sogenannten Interferenzterm
dar.
interference term
Der Vergleich mit unserem Elektronenexperiment läßt folgenden Schluß
zu.
Hypothese. Die Wellenfunktion ψ(x,t) liefert die Wahrscheinlichkeitsverteilung
Conclusion:
ϱ(x,t)=|ψ(x,t)| 2 (2.2)

Hypothesis: The wave function ψ(x, t) gives the probability distribution
ρ(x, t) =|ψ(x, t)| 2 that an electron occupies the position x
important: superposition of the wave function
Remarks:
1. Each electron makes a local impact on the photographic plate. ρ(x, t) is not
the charge distributionof the elektron, but probability distribution.
2. Interference pattern is even obtained, if each electron enters separately.
We are searching for a theory for the wave function ψ (and thus a statistical description).
This theory should should reduce to classical mechanics in the limit of
macroscopic objects.

Anmerkung: ∂t ψ(x,t)=Dψ(x,t)+q,
Würde in der Gleichung eine Inhomogenität q auftreten, also z. B.
so hätte man
Schrödinger so hätte ∂ Zman
Equation Z for Free Particles
∂t d
ψ(x,t)=Dψ(x,t)+q,
Z
Z
d 3 x |ψ(x,t)| 2 = d 3 x ( ˙ψψ ∗ + ψ ˙ψ ∗ )
so hätte dt man
Z
Z Z Z
Z Z
d
An equation d 3 x of |ψ(x,t)| motion 2 = for = ψ(x, d=
3 x d( 3 t) x
dt
˙ψψd ((Dψ)ψ ∗ should 3 x + ((Dψ)ψ ψ ˙ψ ∗ ) satisfy + ψ(Dψ) ∗ + the ψ(Dψ) ∗ following )+
∗ d)+
3 x basic (qψd ∗ demands:
3 + x ψq (qψ ∗ ) ∗ . + ψq ∗ ) .
Z
Z
Falls
1.
D
It should
der Differentialoperator
be a first
=
order
d 3 x ((Dψ)ψ
differential
der Schrödinger-Gleichung ∗ + ψ(Dψ)
equation ∗ )+
ind 3 time
x (qψist, so ∗ + ergibt
that
ψq ∗ )
ψ(x,
. sich
t)
nach
willbedetermined
by the initial
dem
(j,
condition
Stromdichte;
ψ(x,0).
Gaußschen lntegralsatz (j, Stromdichte; siehe siehe Gleichungen Gleichungen (2.58)–(2.60)) (2.58)–(2.60))
Falls D der Differentialoperator der Schrödinger-Gleichung ist, ergibt sich nach dem
2. It should Z Z
GaußschenZ
be linear
lntegralsatz (j, Z
in ψ in order for the principle of superposition.
Stromdichte; siehe Gleichungen (2.58)–(2.60))
Z df .
3. j + Z d 3 x 2Re{qψ ∗ } .
= It −should df be. homogenous, j + d 3 x 2Re{qψ so that ∗ } .
= −
O df . j + d 3 x 2Re{qψ ∗ } .
O
O
Der ersted Term 3 x|ψ(x, istt)| 0, 2 wenn =1(normalization)
ψ rasch genug abfällt, z. B.: ψ ∈ L 2 , jedoch ist der zweite
Summand Der erste Term i. a. ist ungleich 0, wennNull.
ψ rasch genug abfällt, z. B.: ψ ∈ L 2 , jedoch ist der zweite
Summand holdsi. for a. i. a. all ungleich times, Null. since Null. the probability to find the particle somewhere in space
iv) is 1. Schließlich sollen die ebenen Wellen
iv) Schließlich sollen die ebenen Wellen
4. iv) plane Schließlich waves { sollen die ebenen )
{
) / } / Wellen }
ψ(x,t)=C exp i
(p .
ψ(x,t)=C exp i
(p {. x − p2
x − p2
2m
2m t t
}
(p . x − p2
most dt simplest d 3 x |ψ(x,t)| case: 2 free = dparticle, 3 x ( ˙ψψ ∗ + no ψ ˙ψ ∗ forces )
Falls D der Differentialoperator der Schrödinger-Gleichung ist, ergibt sich nach dem
Der erste Term ist 0, wenn ψ rasch genug abfällt, z. B.: ψ ∈ L 2 , jedoch ist der zweite
ψ(x,t)=C exp
i
2m t ) /
Lösungen should der be Gleichung solution of sein. sein. theFür equation. Für ebene ebene ForWellen plane gilt: waves, gilt: we have:
Lösungen der Gleichung p 2 sein. Für 2 ebene Wellen gilt:
∂
i p 2
2m i 2
2m ∇2 ψ(x,t) .
∂t ψ(x,t)=− i 2m ψ(x,t)= i 2m ∇2 ψ(x,t) .
∂
∂t ψ(x,t)=− i 2m ψ(x,t)= i 2m ∇2 ψ(x,t) .
p 2
Aus den Postulaten (i) (i) bis bis (iv) (iv) erhalten erhalten wir also wir also
The unique
i 2
ψ(x,t)=−
∂t 2m ∇2 ψ(x,t) . (2.4)
i ∂ partial differential equation, which fullfills postulates 1) - 4), is:
2
Aus denψ(x,t)=− Postulaten (i)
∂t 2m ∇2 bis ψ(x,t) (iv). erhalten wir also
(2.4)
Dies ist die zeitabhängige Schrödinger-Gleichung für freie Teilchen.
Dies ist die zeitabhängige Schrödinger-Gleichung für freie Teilchen.
i ∂ 2
ψ(x,t)=−
∂t 2m ∇2 ψ(x,t) . (2.4)
2.3 Superposition von ebenen Wellen
Dies ist die zeitabhängige Schrödinger-Gleichung für freie Teilchen.
2.3 Superposition von ebenen Wellen
2
time dependent Schrödinger equation for free particles

i ∂ ∂t ψ(x,t)=− 2m ∇2 ψ(x,t) . (2.4)
Superposition of plane waves
Dies ist die zeitabhängige Schrödinger-Gleichung für freie Teilchen.
Question: How can we construct localized states from plane
waves?
2.3 Superposition von ebenen Wellen
plane waves
Die ebenen Wellen
ψ(x,t)=C exp
{ i
(p . x − p2
2m t )}
have haben spatial eine homogenous räumliche homogene probability Wahrscheinlichkeitsdichte density |ψ(x, t)| 2 |ψ(x,t)| = C 2 2 = C 2 .
Denken wir uns das Teilchen in eine Box mit Volumen V eingeschlossen,
ergibt sich aus der Normierungsforderung ∫ particle V d3 xC 2 = 1 für C der Wert
C =1/ √ in a box with volume V =⇒
V .
normalization d 3 xC 2 =1 =⇒ C = √ 1
V
V
V →∞ ?

Lokalisierte Zustände, d. h. solche mit räumlich konzentrierter Ausdeh
nung,
localized Lokalisierte erhalten
states are Zustände, wir durch
obtained d. Superposition
by h. superposition:
solche mit räumlich (Überlagerung) konzentrierter ebener Ausdehnung,
erhalten ∫wir durch Superposition (Überlagerung) ebener Wellen 1 :
Wellen 1 :
∫
d 3 { )}
p
d 3 { i
ψ(x,t)=
)}
p
i
(p
ψ(x,t)= (2π)
(p
(2π) 3 ϕ(p)exp 3 ϕ(p)exp . x − p2
. x − p2
2m t 2m t . (2.5)
. (2.5)
} {{ }
}
(Dreidimensionales
{{
Wellenpaket)
}
(Dreidimensionales Wellenpaket)
Besonders
Besonders
especially simple einfach
einfach
for
werden
a werden one-dimensional die Verhältnisse
die Verhältnisse
Gaussian
für
wave für
ein
packet ein eindimensionales Gauß
eindimensionales Gauß-
sches Wellenpaket, d. d. h. h.
ϕ(p) =A exp{−(p − p 0 ) 2 d 2 / 2 } . (2.6)
ϕ(p) =A exp{−(p − p 0 ) 2 d 2 / 2 } . (2.6)
(Die Verallgemeinerung auf drei Dimensionen ist trivial, weil das dreidimen
sionale Gaußsche Wellenpaket exp{−(p − p 0 ) 2 d 2 / 2 } in drei eindimensionale
Gauß-Funktionen faktorisiert.) Zur Berechnung von (2.5) führen wir vorüber
gehend die Abkürzungen
(Die 18 Verallgemeinerung 2. Wellenfunktionauf und drei Schrödinger-Gleichung
Dimensionen ist trivial, weil das dreidimensionale
(the three-dimensional Gaußsche Wellenpaket Gaussian wave exp{−(p packet is product − p 0 ) 2 of d 2 the / 2 one-dimensional } in drei eindimensionale
ones)
Gauß-Funktionen A = 4√ 8πd 2 . faktorisiert.) Zur Berechnung von (2.5) führen wir vorübergehend
(2.13)
We obtain
die
for
Abkürzungen
the probability density (exercise ???)
Damit erhalten wir insgesamt
d2
2 +i t
2m , b = d2 p 0
2 +i x 2 , c = d2 p 2 0
2 (2.7)
a = d2
2 +i t
2m , b = d2 p 0 {
2 +i x 2 , c = d2 p 2 0
|ψ(x, t)| 2 1
=
ein, mittels derer d(2.5) √ 2π(1 und + ∆(2.6)
2 ) exp −
(x − }
vt)2
2d 2 (1 + ∆ 2 . (2.14)
)
ψ(x, t) =
A ∫ { (
dp exp −a p − b ) 2 }
group
also auch
velocity
im
v
Ortsraum
= p + b2
2π
a a − c ψ(x, t) =
A
0 ∫ eine Gauß-Verteilung. { ( ) 2
Das Maximum } des Wellenpaketes
bewegt sichm mit , der ∆ = t
√ dp
Gruppengeschwindigkeit 2md
{ exp
2
2
−a}
+ b2 v
a − = c p 0 /m = ∂E/∂p| p0 wie
ein klassisches Teilchen, während die einzelnen superponierten ebenen Wel-
ein, mittels derer (2.5) und (2.6)
2π
p − b a
2 (2.7)

ketes bewegt sichlen mitdie derPhasengeschwindigkeiten Gruppengeschwindigkeitv ph = = p 0 E/m p /p
wächst mit der Zeit t; das bedeutet, daß die Funktion |ψ| 2 = ∂E/∂p| p/2m p0 besitzen. wie Die G
2.3 Superposition von ebenen Wellen 17
ein klassisches Teilchen, wächst mit während der Zeit diet; einzelnen das bedeutet, superponierten daß die Funktion imebenen Laufe|ψ| Wellen
flacher die Phasengeschwindigkeiten wird, daß sie auseinanderfließt“,
der 2 imZeit
Laufe d
also auch im Ortsraum
ihre Lokalisation
eine Gauß-Verteilung.
also abnimmt.
Das Maximum
Lokalisierte Zustände, flacher |ψ| d. ” h. wird, 2 solche getsdaß flatter. mit ketes vsie ph räumlich bewegt = auseinanderfließt“, E p /p konzentrierter = p/2m besitzen. Die Größe ∆
wächst Ferner mit interessieren der Zeit t; dasuns bedeutet, Mittelwert ” sich mit Gruppengeschwindigkeit Ausdehnung,
erhalten wir durchFerner Superposition interessieren ein
ihre Lokalisation v also = p
daß die und Funktion Schwankungsquadrat |ψ| 2 0
abnim /m =
(Überlagerung)
klassisches uns Teilchen, Mittelwert ebener Wellen
während 1 und : imdie Schwankungsquadrat Laufe einzelnen der des Zeit superponierten
Ortes de
flacher für die wird, vorliegende ∫
daß d 3 für sie Wahrscheinlichkeitsdichte { )}
p dieauseinanderfließt“, vorliegende Wahrscheinlichkeitsdichte ihre Lokalisation (2.14). Deralso Mittelwert (2.14). abnimmt. Der des Mittelwert Ortes de
berechnet sich zu ” i
ψ(x,t)=
Ferner interessieren (2π) berechnet 3 ϕ(p)exp len (p . x − p2 Phasengeschwindigkeiten
unssich Mittelwert zu 2m t v ph = E p /p = p/2m besitzen.
wächst mit
. (2.5)
und der Schwankungsquadrat Zeit t; das bedeutet, daß des die Funktion Ortes |ψ| 2 im L
}
für die vorliegende ∫ ∞
{{
Wahrscheinlichkeitsdichte ∫ ∞ flacher wird, } daß
(Dreidimensionales Wellenpaket)
(2.14). sie auseinanderfließt“, Der Mittelwert ihre des Ortes Lokalisation also
”
berechnet 〈x〉 = sich |ψ(x, zu t)| 〈x〉 2 Ferner
x=
dx |ψ(x, t)| 2 interessieren uns Mittelwert und Schwankungsquad
x dx
∆ increases in time =⇒
wave function spreads out, localisation is reduced.
closer look on the average and root-mean-square deviation of position for the present PDF.
Besonders einfach
∫
−∞
∞ werden die Verhältnisse für ein eindimensionales Gaußsches
Wellenpaket, d. h.
〈x〉 =
∫+∞
|ψ(x, t)| 2 −∞ berechnet sich zu
x dx ∫+∞
∫+∞
+∞
ϕ(p) =A exp{−(p − p 0 ) 2 d 2 / 2 ∫
} . ∞
∫ (2.6)
−∞
= dx|ψ(x, t)| = 2 〈x〉 =
(x −dx|ψ(x, vt)+ t)| 2 |ψ(x, t)|
(x − vt)+
2 x dx
(Die Verallgemeinerung auf drei Dimensionen ist trivial, weil das dreidimensionale
Gaußsche Wellenpaket exp{−(p
∫+∞
∫+∞
−∞
−∞
= dx|ψ(x, t)| 2 −∞ − p 0 ) 2 d 2 −∞
/ 2 } in drei eindimensionale
(x − vt)+ dx|ψ(x, t)| 2 −∞
Gauß-Funktionen faktorisiert.) Zur Berechnung von
∫+∞
(2.5) führenvt wir= vorübergehend
die Abkürzungen = 0, odd function in (x-vt) =
vt .
−∞
−∞
ist. Für das Schwankungsquadrat erhält man
a = d2
2 +i t
2m , b = d2 p 0
2 +i x 2 , c = d2 −∞
p 2 0
2 (2.7)
dx|ψ(x, t)| 2 vt dx|ψ(x, = vt . t)| 2 vt = vt .
Das erste Integral
Das
verschwindet,
erste Integral
da
verschwindet, dx|ψ(x,
|ψ(x, t)| 2 eine
da t)| |ψ(x, 2 −
gerade
t)| vt)+
2 Funktion
einedx|ψ(x, geradet)| in (x−vt)
Funktion 2 = vt . in
ist. Für das Schwankungsquadrat erhält man −∞
Das erste Integral verschwindet, da |ψ(x, t)| 2 eine gerade Funktion in (x−vt)
(∆x) 2 (∆x)
= 〈(x −〈x〉) 2 〉
2 = 〈(x −〈x〉) 2 〉
ist.
ein, mittels
Für das
derer
Schwankungsquadrat
(2.5) und (2.6) ∫ ist. erhält man
+∞
Für
+∞
(∆x) 2 = 〈(x−∞ −〈x〉)
=
dx|ψ(x, 2 〉 t)|2 −∞
= (x − dx|ψ(x, das Schwankungsquadrat erhält man
vt) 2 t)|2 (x − vt) 2
∫
∫ ∫ +∞
+∞
−∞ dx|ψ(x, = d 2 (1 + ∆ 2 +∞
) .
−∞
=
dx|ψ(x, t)|2 − t)|2 vt)
−∞ 2 dx|ψ(x, = d 2 (1 + ∆ 2 ) .
ψ(x, t) =
A ∫ { (
dp exp −a p − b ) 2 }
(∆x) 2
+ b2
2π
a a − c = 〈(x −〈x〉) 2 〉
∫ +∞ t)|2
Hier ∫ +∞ benützten
Hier benützten wir −∞(2.9) dx|ψ(x, wir (2.9) und d 2 (1 deren + ∆ 2 = A √ { }
−∞
π b
2
=
dx|ψ(x, t)|2 (x − vt) 2
∫
) Ableitung . nach α:
2π a exp a − und c +∞
t)|2 −∞
deren Ableitung nach dx|ψ(x, = d 2 (1 + ∆ 2 ) .
(2.8)
α:
t)|2 Derivative
ergeben, wobei wir das bekannte
Hier benützten
∫ ∞ wir (2.9)
∫ ∞ Gauß-Integral Hier benützten with respect
und deren Ableitung nach α:
∫ dx x 2 e −αx2 = √ dx x 2 e −αx2 = √ wir (2.9) tound α: deren Ableitung nach α:
∫ ∞
√ ∫ ∞ π/2α 3/2 π
.
∞ dx e −αx2 = π/2α 3/2 .
dx x 2 α −∞
e −αx2 = √ dx x 2 e −αx2 = √ π/2α 3/2 (2.9) .
−∞
π/2α 3/2 . −∞
root-mean-square deviation
This follows from
−∞
für die vorliegende Wahrscheinlichkeitsdichte (2.14). Der Mittelw
∫
+∞
Das erste Integral verschwindet, da |ψ(x, t)| 2 eine gerade Funkt

with
α =
Thus we have:
1
2d 2 (1 + ∆ 2 )
=⇒ (∆x) 2 = d 2 (1 + ∆ 2 )
position expectation value:
position uncertainty:
x = vt
∆x = d √ 1+∆ 2
examples:
i) macroscopic particle
mass m = Nm p ≈ 10 23 × 10 −24 g = 10 −1 g
∆= t
2md 2 ≈ 10−26 t
d 2
ii) α − particle
∆ = (10 −27 /2 · 4 · 1.6 · 10 −24 ) t
d 2 ≈ 10−4 t
d 2
∆x = d = 10 −11 cm at t =0
=⇒ ∆=1att ≈ 10 −18

Whether ot not the spreading is significant, depends on the problem:
α-particle with speed v = c/30 =⇒ distance 10 −9 cm nuclear radius ≈ 10 −12 cm
=⇒ during the collision with a nucleus
the trajectory can be described classically
Java-Applet

der Wahrscheinlichkeitsdichte nimmt mit der Zeit zu
Probability Distribution for a Measurement of Momentum
position space:
2.4 Wahrscheinlichkeitsverteilung
für eine Impulsmessung
looking for:
Nun beschäftigt uns die Frage, welche Wahrscheinlichkeitsdichte die Realisie
momentum space:
rung
probability
bestimmter
to
Impulswerte
find particle
beschreibt.
with momentum
Im Ortsraum
p
war die Wahrschein
lichkeit, ein Teilchen am Ort x im Volumen d 3 in d 3 p
=
x zu finden, gegeben durch
ϱ(x,t)d 3 W (p, t)d 3 p =?
x = |ψ(x,t)| 2 d 3 x. Entsprechend werde die Wahrscheinlichkeit, da
20 2. Wellenfunktion
Teilchen mit Impuls p in d 3 und Schrödinger-Gleichung
p anzutreffen, dargestellt durch W (p,t)d 3 p. Auch
hier wird die Gesamtwahrscheinlichkeit auf 1 normiert:
Drückt ∫ man nun in Analogie zu (2.5) ψ(x,t) durch seine Fourier
normalization mierte d 3 (siehe pW(p,t)=1. Anhang A) ϕ(p,t) aus, also
(2.17
Fourier-Trafo
probability to find particle at x in d 3 x
= ρ(x, t)d 3 x = |ψ(x, t)| 2 d 3 x
ψ(x,t)=
dann bekommt man damit
∫
d 3 x |ψ(x,t)| 2
=
∫
d 3 x
∫
∫
d 3 p
(2π) 3 ϕ(p,t)eip . x/
,
d 3 p ∫ { i
d 3 p ′ exp (p − p ′ ) . x}
ϕ(p,t)ϕ ∗ (p ′ ,t)

∫
∫ d∫
3 p (2π) 3
.
∫ψ(x,t)=
x/
dann bekommt man damit
dann ∫ bekommt (2π) man 3 ϕ(p,t)eip ,
damit
d
=⇒
3 = d 3 d 3 ∫
}
p
i
x
x |ψ(x,t)| 2
d 3 x |ψ(x,t)|
(2π) 2 6 d 3 p exp{ ′ (p − p′ ) . x ϕ(p,t)ϕ ∗ (p ′ ,t)
dann bekommt d 3 x man |ψ(x,t)| damit
∫ ∫ ∫ ∫ ∫
∫
2
= d 3 d 3 ∫
}
=
p
i
d x
(2π) 6 d 3 p exp{ 3 x d 3 d 3 ∫
}
=
|ψ(x,t)| x d p
∫ ∫
′ (p − p′ ) . x
∗ (p ′ = d 3 d 3 ∫
}
(2π) 2
p
x
∫ (2π)
= d 3 d 3 p ′ 6 d 3 p exp{ 6 d 3 p exp{ 3 d 3 p ′
p
i ′
′ (p − i p′ ) . x ϕ(p,t)ϕ ∗ (p ′ ,t)
(p − p′ ) . x ϕ(p,t)ϕ ∗ (p ′ ,t)
wegen ∫
∫
∫
∫
}
p
∫
i
= d x
(2π) 3 δ(3) (p − p ′ )ϕ(p,t)ϕ ∗ (p ′ , (2.18)
= d(2π) 3 p
6 d 3 p d ′ 3 p exp{ 3 d 3 p ′
′
wegen
(2π) 3 δ(3) (p − p ′ )ϕ(p,t)ϕ − p′ ) . x ϕ(p,t)ϕ ∗ (p ′ ,t)
∫
p
}
∗ (p ′ ,t) , (2.18)
∫ ∫ i
d 3 x exp{
= wegen
∫
3 d 3 p ′
p (p − (2π) }
∫ i
d 3 x exp{
i (p − p′ ) . }
x =(2π) 3 δ (3) (p − p ′ ) .
d 3 x exp{ 3 δ(3) (p p′ ) . x =(2π) 3 δ (3) (p − p ′ ) .
− p ′ )ϕ(p,t)ϕ ∗ (p ′ ,t) , (2.18)
∫
}
wegen due to i
Folglich d 3 x exp{
ergibt
(p − p′ ) . x =(2π) 3 δ (3) (p − p ′ ) .
∫ (p sich −
dFolglich 3 x exp{ p′ aus ) . x(2.18)
=(2π) 3 δ (3) (p − p ′ ) .
}
∫ergibt i sich aus (2.18)
Folglich ∫ (p − ∫
sich p′ ) . x =(2π) 3 δ (3) (p − p ′ ) . (Exercise ???)
d 3 x |ψ(x,t)| aus (2.18) 2 = ∫ d 3 1
p
∫ ∫
d 3 x |ψ(x,t)| ∫ 2 =
∫ (2π)
d 3 1
3 |ϕ(p,t)|2
p
(2π) 3 |ϕ(p,t)|2 . (2.19)
Folglich ergibt} sich
}
daus 3 x |ψ(x,t)| (2.18) {{ 2 =
{{
d 3 1
=⇒ d 3 x |ψ(x,t)| 2 = d 3 p1
}
(2π) 3 |ϕ(p,t)|2 }
. (2.19)
(Parsevalsches ∫ Theoremp
(Parsevalsches } ∫ der
Theorem der {{(2π) Fourier-Transformation)
Fourier-Transformation) }
(Parsevalsches d 3 x |ψ(x,t)| 2 Theorem = d 3 1
3 |ϕ(p,t)|2
} {{
p
}
der Fourier-Transformation)
(2π)
Das legt für die Wahrscheinlichkeitsdichte 3 |ϕ(p,t)|2 . (2.19)
(Parsevalsches
}
Theorem
{{
der Fourier-Transformation)
im } Impulsraum folgende Definition
nahe: Motivation (Parsevalsches nahe: Das legtfor fürprobability die Theorem Wahrscheinlichkeitsdichte der density Fourier-Transformation)
momentum im Impulsraum space folgende Definition
nahe:
1
Das legt W für (p,t)= W die Wahrscheinlichkeitsdichte
(2π)
1 3 |ϕ(p,t)|2 . im Impulsraum folgende Definition (2.20)
nahe: W (p,t)=
(2π) 3 |ϕ(p,t)|2 . (2.20)
1
W (p,t)= Dies ist auch 1 im Einklang damit, daß für eine ebene Welle mit Impuls p 0 die
W (p,t)= Fourier-Transformierte Dies ist auch im Einklang ϕ(p,t) damit, nurdaß für für p = eine p 0 verschieden ebene Wellevon mit Null Impuls ist. p 0 die
Fourier-Transformierte
(2π) 3 |ϕ(p,t)|2 . (2.20)
Kehren wir nun zumϕ(p,t) Gaußschen nur für Wellenpaket p = p 0 verschieden in einer von Dimension Null ist. ((2.5),
Dies istspezialisiert auch
Kehren
im Einklang
wir auf nun eine damit,
zum Dimension, Gaußschen
daß für und eine (2.6)) Wellenpaket
ebene zurück. Welle
inFür einer
mit diesen Impuls
Dimension speziellen p
((2.5),
0 die Fall
dann bekommt man damit
wegen
Folglich ergibt sich aus (2.18)
(2π) 3 δ(3) (p − p ′ )ϕ(p,t)ϕ ∗ (p ′ ,t) , (2.18)
(2π) 3 δ(3) (p − p ′ )ϕ(p,t)ϕ ∗ (p ′ ,t) , (2.18)
. (2.19)
. Parseval identity (2.19)
Das legt für die Wahrscheinlichkeitsdichte im Impulsraum folgende Definition
Das legt für die Wahrscheinlichkeitsdichte im Impulsraum folgende Definition
nahe:
(2π) 3 |ϕ(p,t)|2 . (2.20)
(2π) 3 |ϕ(p,t)|2 . (2.20)
Dies ist auch im Einklang damit, daß für eine ebene Welle mit Impuls p 0 die
Fourier-Transformierte ϕ(p,t) nur für p = p
Dies ist auch im Einklang damit, daß für eine ebene 0 verschieden von Null ist.
Welle mit Impuls p 0 die
Kehren wir nun zum Gaußschen Wellenpaket in einer Dimension ((2.5),

(2π)
0
Fourier-Transformierte ϕ(p,t) nur für p = p 0 verschieden von Null ist.
Dies Kehren ist auch wirimnun Einklang zum Gaußschen damit, daß Wellenpaket für eine ebene in einer Welle Dimension mit Impuls ((2.5), p 0 die
spezialisiert Gaussian
Fourier-Transformierte
wave auf packet eine Dimension, (in one
ϕ(p,t)
dimension)
nur und für (2.6)) p = zurück. p 0 verschieden Für diesen von speziellen Null ist. Fall
erhält Kehren man die wirWahrscheinlichkeitsdichte
nun zum Gaußschen Wellenpaket in einer Dimension ((2.5),
spezialisiert auf eine Dimension,
W (p, t) = 1
√ und (2.6)) zurück. Für diesen speziellen Fall
erhält man die Wahrscheinlichkeitsdichte
2 d
2π |ϕ(p)|2 =
π exp{−2(p − p 0) 2 d 2 / 2 } . (2.21)
DieseW ist (p, zeitunabhängig, t) = 1
√
2 d
2π |ϕ(p)|2 da= wir
π
freie
exp{−2(p Teilchen − betrachten. p 0) 2 d 2 / 2 Mit } . (2.21) kann (2.21)
note that W (p, t) =W (p) istimeindependent(freeparticle)
der mittlere Impuls zu
Diese ist∫zeitunabhängig, ∫da wir freie Teilchen betrachten. ∫ Mit (2.21) kann
average der〈p〉 mittlere = momentum dpImpuls W (p, t)p zu = dp W (p, t)(p − p 0 )+ dp W (p, t)p 0 = p 0
∫
∫
∫
berechnet 〈p〉 = werden, dp W und (p, t)p das = zugehörige dp W (p, Schwankungsquadrat t)(p − p 0 )+ dp W (p, lautet t)p 0 = p 0
2.4 Wahrscheinlichkeitsverteilung für eine Impulsmessung 21
berechnet werden, und das
∫
zugehörige Schwankungsquadrat
( )
lautet
2
(∆p) 2 = 〈(p − p 0 ) 2 〉 = dp W (p, t)(p − p 0 ) 2 = .
2d
Also:
=⇒ p = p 0 , ∆p =
2d
=⇒ ∆x∆p =
1+∆2 ≥ 2
2
Impulsmittelwert: 〈p〉 = p 0 (2.22)
Impulsunschärfe: ∆p = /2d . special case of uncertainty relation (2.23)
Zusammen mit (2.16) führt dies zu

Wie wir sahen, kann man Impulsmittelwerte, -unschärfen etc. im Impulsraum
mit Hilfe der in (2.20) definierten Wahrscheinlichkeitsdichte W (p,t) bestimmen.
Lassen sich diese auch im Ortsraum berechnen? Betrachten wir dazu
Beim beschriebenen Experiment können Ort und Impuls gleichzeitig prinzipiell
nicht genauer bestimmt werden als es diese Beziehung erlaubt.
Example Zwei Zahlenbeispiele I bullet mögen v = die 10 5 Unschärferelation cm/sec (supersonicillustrieren: speed) Die Unschärferelation
gilt assumption: auch für makroskopische ∆v = 10 −2 cm/sec Körper. =⇒ Betrachten ∆p = m × wir 10z. −2 B. cm/sec ein
Geschoß der Geschwindigkeit=⇒ v =10 ∆x 5 =1/m cm/sec × (Überschallgeschwindigkeit)
10 2 sec cm −1 ≈ 1/m × 10 −25 gcm −1
und einer Unsicherheit in der Geschwindigkeit von ∆v =10 −2 cm/sec, was
einem ∆p = m × 10 −2 cm/sec entspricht. Die Unschärferelation sagt nun,
daß die gleichzeitige Ortsbestimmung nur mit einer Unschärfe von
insignificant: mass 10 −6 kg = 10 −3 g =⇒ ∆x ≈ 10 −22 cm ≈ 10 −14 atomic radii
∆x =(1/m) × 10 2 sec cm −1 ∼ = (1/m) × 10 −25 gcm
möglich ist, die mit wachsender Masse unbedeutender wird. Selbst bei einer
Masse Example von nur II 10 −6 kg = 10 −3 g ist ∆x ∼ = 10 −22 cm ∼ = 10 −14 Atomradien!
Anders hingegen für Elektronen im Atom, für die
∆p ∼ = mv ∼ = 10 −27 × 10 10 /137 g cm/sec und ∆x ∼ = a ∼ = 10 −8 cm
a: Bohr radius
(a: Bohrscher Radius) ist, was an die Grenze des durch die Unschärferelation
Erlaubten stößt. Da die angegebenen Werte den Dimensionen der untersuchten
Effekte entsprechen, haben im atomaren Bereich die Unschärfen
erhebliche Bedeutung.
2.4.2 Impuls im Ortsraum

men. Lassen sich diese auch im Ortsraum berechnen? Betrachten wir dazu
Momentum in position space
den uns bekannten Mittelwert des Impulses
2.4 Wahrscheinlichkeitsverteilung für ei
∫
d 3 p
∫
〈p〉 =
(2π)
2.4 3 Wahrscheinlichkeitsverteilung ϕ(p,t)∗ p ϕ(p,t) . für eine Impulsmessung d 3 ∫
∫
p (2.25)
〈p〉 =
23
∫
d
Für〈p〉 ϕ(p,t) = wird 3 ∫
∫ (2π) 3 d 3 x ′ e ip . x ′ / ψ ∗ (x ′ ,t) p d 3 x
p
die Fourier-Transformierte eingesetzt und wir erhalten
(2π) 3 d 3 x ′ e ip .
∫
x ′ / ψ ∗ (x ′ ,t) p d 3 x e −ip . d x/ 3 ∫
∫ [
p
= ψ(x,t)
∫
d 3 ∫
∫
(2π)
p
=
(2π) 3 d 3 x ′ e ip . x ′ / ψ ∗ (x ′ ,t) d 3 x
[− 3 d 3 x ′ e ip . x ′ / ψ ∗ (x ′ ,t) d 3 x
∫
∫ ]
(
i ∇ . x/
= d 3 x e−ip d 3 x ′ ψ(x,t)
1
(2π)
∫ ∫
( )
3 ψ∗ (x ′ ,t)
i ∇ψ(x,t
∫
}
= d 3 x d 3 x ′ 1
(2π) 3 ψ∗ (x ′ i
,t)
i ∇ψ(x,t) × d 3 p exp{
(x′ − x) . p .
∫
}
i
× d 3 p exp{
(x′ − x) . p .
In der vorhergehenden Zeile haben wir unter der Vor
Unendlichen stark genug abfällt, daß die Randterm
In der vorhergehenden Zeile haben wir unter
integriert.
der Voraussetzung,
Benützen wir,
daß
daß
ψ(x)
das
im
letzte Integral gle
partial integration dann finden wir schließlich
Unendlichen stark genug abfällt, daß die Randterme also Null sind, partiell
∫
integriert. Benützen wir, daß das letzte Integral gleich (2π) 3 δ 3 (x ′ − x) ist,
〈p〉 = d
dann finden wir schließlich
3 x ψ ∗ (x,t) i ∇ψ(x,t) .
Thus: ∫ p −→ ∇
〈p〉 = d 3 x ψ ∗ (x,t) momentum operator in position space
i ∇ψ(x,t) .
Wegen dieses Zusammenhanges
(2.26)
bezeichnet man (/
i rator im Ortsraum:
Wegen dieses Zusammenhanges bezeichnet man p −→ (/i)∇ ∇ als Impulsoperator den Impulsoperator
im Ortsraum:
im Ortsraum .
i
p −→ ∇ Impulsoperator im Ortsraum 2.4.3 . Operatoren und Skalarprodukt
(2.27)

Operators and Scalar Product
p → i
∇ was the first example that physical quantities are represented by operators
Consider some properties of operators.
Function space: : L 2 (due to normalisation)
Consider only operators A, forwhichwehave:Letψ(x) ∈ L 2 =⇒ Aψ(x) ∈ L 2
A is named linear Operator, if it holds:
let Aψ 1 = φ 1 , Aψ 2 = φ 2 =⇒ A(c 1 ψ 1 + c 2 ψ 2 )=c 1 φ 1 + c 2 φ 2 mit c 1 , c 2 ∈ C
simple operations with linear operators
cA : cAψ := c(Aψ)
A + B : (A + B)ψ = Aψ + Bψ
1: 1ψ = ψ
0: 0ψ =0

Generally, operators are not commutative, AB = BA
Commutator [A, B] =AB − BA
Examples:
f (x),
⇒
f (x),
∂
ψ = f
∂x j
∂
∂x j
∂
∂x j
ψ −
= − ∂
∂x j
f (x)
∂
∂x j
f
ψ − f
∂ ∂
ψ = − f
∂x j ∂x j
ψ
special case: f (x) =x i ⇒
x i ,
∂
∂x j
= −δ ij
[x i , x j ]=0
∂ ∂
,
∂x i ∂x j
=0
therefore: basic commutators of position and momentum operators:
[x i , x j ]=0 ; [p i , p j ]=0 ; [x i , p j ]=iδ ij

Scalarprodukt: φ, ψ ∈ L 2
properties:
(φ, ψ) :=
d 3 x φ ∗ (x)ψ(x)
(φ, ψ) ∗ =(ψ, φ)
(φ, c 1 ψ 1 + c 2 ψ 2 )=c 1 (φ, ψ 1 )+c 2 (φ, ψ 2 )
(c 1 φ 1 + c 2 φ 2 , ψ) =c ∗ 1 (φ 1 , ψ)+c ∗ 2 (φ 2 , ψ)
(φ, φ) ≥ 0 ; (φ, φ) =0⇐⇒ φ =0
Operators in the scalar product (φ, Aψ) =
dx 3 φ ∗ (x)Aψ(x)
A † is called “adjoint operator” to A if: (A † φ, ψ) =(φ, Aψ)
i.e.,
dx 3 (A † φ) ∗ ψ =
dx 3 φ ∗ Aψ holds for arbitrary φ, ψ
Example: A = ∂
∂x i
⇒ A † = − ∂
∂x i

A is called Hermitian (self-adjoint) if A † = A
Example: A = ∂2
∂x 2 i
= A †
(AB) † = B † A † ,because:
dx 3 ((AB) † φ) ∗ ψ =
dx 3 φ ∗ ABψ =
dx 3 (A † φ) ∗ Bψ =
dx 3 (B † A † φ) ∗ ψ
Identities (Exercises ???):
[AB, C] =A[B, C]+[A, C]B , [A, B] † =[B † , A † ]
Baker - Hausdorff:
e A Be −A = B +[A, B]+ 1 2! [A,[A, B]] + ... where eA =
∞
k=0
= 1 k! Ak
If [[A, B], A] =0=[[A, B], B] then:
e A e B = e B e A e [A,B]
e A+B
= e A e B e −[A,B]/2

Operators and Schrödinger Equation
plane wave ψ(x, t) =C exp(i(p · x − Et)/)
momentum: p → i ∇
analog for energy: E → i ∂ ∂t
classical energy-momentum relation for free particles:
E = p2
2m −→ i ∂ ∂t ψ = − 2
2m ∇2 ψ
Schrödinger equation for free particles
consider particle in potential V and Hamiltonian
H = p2
2m + V (x)
E = p2
2m + V (x) → i ∂ ∂t ψ =
− 2
2m ∇2 + V (x)
ψ
=⇒ Schrödinger equation of a particle in a potential V (x)
i ∂ ∂t
ψ(x, t) =Hψ(x, t) , H
= − 2
2m ∇2 + V (x)

Postulates of QM (preliminary version)
1. The state of a system is described by the wave function ψ(x, t).
| ψ(x, t) | 2 d 3 x = expresses probability of finding the particle at time t at
position x in d 3 x.
2. Quantum mechanically, operators A, B, ... are assigned to the physically measurable
quantities (observables).
3. Average values of operators ψ(x, t) are given by
A = d 3 xψ ∗ (x, t) A ψ(x, t)
4. Time evolution of the states is governed by the Schrödinger equation:
i ∂ ∂t
ψ(x, t) =Hψ(x, t) ; H
= − 2
2m ∇2 + V (x)

Many-Particle Systems
seek Schrödinger equation for system of N particles
state is described by wave function
ψ(x 1 , x 2 ,...,x N , t) , x i coordinates of the ith particle
|ψ(x 1 , x 2 ,...,x N , t)| 2 d 3 x 1 d 3 x 2 ... d 3 x N = probability to find particle i at time t
at position x i in volume d 3 x i
classical energy
E = p2 1
2m 1
+ p2 2
2m 2
+...+ p2 N
2m N
+ V (x 1 , x 2 ,...,x N )
=⇒ Schrödinger equation for N-particle system
i ∂
∂t ψ(x 1,...,x N , t) =
− 2
∇ 2 1 − ... −
2
∇ 2 N + V (x 1 , x 2 ,...,x N )
2m 1 2m N
∇ i =Nablawithrespecttox i , i = 1, ... , N
ψ

Wir gehen von der Schrödinger-Gleichung 2.6 Das Ehrenfestsche Sinn und dies der der Theorem dazu Fall konjugiert ist. komplexen
Ehrenfest Gleichung Theorem aus:
Wir gehen von der Schrödinger-Gle
Die klassische Newtonsche Mechanik muß als Grenzfall in der Qua
plexen Gleichung aus:
nik enthalten sein. Wir wollen in diesem Abschnitt untersuchen,
classical
i ∂ Sinn dies der Fall ist.
∂t ψ Newtonian = Hψ mechanics = limiting case of QM
Wir gehen von der Schrödinger-Gleichung i ∂ und der dazu konj
plexen Gleichung aus: ∂t ψ = Hψ (2.52a)
but how?
−i ∂ ∂t ψ∗ = Hψ ∗ .
Consider Schrödinger eqn.:
i ∂ ∂t ψ = Hψ
−i ∂ ∂t ψ∗ = Hψ ∗ .
(2.52b)
Für einen linearen Operator A ist
−i ∂ der Mittelwert (= Erwartungswert) im
conj. complex:
Zustand ψ definiert durch ∂t ψ∗ = Hψ ∗ .
∫
average 〈A〉 = valued 3 of x aψ ∗ linear (x,t)Aψ(x,t) operator A in . state ψ:
(2.53)
Für einen linearen Operator A ist de
Zustand ψ definiert durch
∫
Für einen linearen Operator A ist der Mittelwert (= Erwartun
Zustand ψ definiert durch
〈A〉 = d 3 x ψ ∗ (x,t)Aψ(x,t) .
∫
〈A〉 = d 3 x ψ ∗ (x,t)Aψ(x,t) .
temporal change:
Dieser ändert sich mit der Zeit wie folg
Dieser ändert sich mit der Zeit wie∫
folgt: (
d
dt A = d 3 x ˙ψ ∗ A ψ + ψ ∗ Ȧ ψ ∫+ ψ ∗ A(
˙ψ
∫ (
d
d
dt 〈A〉 = d 3 x ˙ψ ∗ Aψ + ψ ∗ ∂A )
dt 〈A〉 = d 3 x ˙ψ ∗ Aψ + ψ ∗ ∂A
∂t ψ + ψ∗ A ˙ψ . ∂t ψ +
dt 〈A〉 =
d 3 x
˙ψ ∗ Aψ + ψ ∗ ∂A )
i ∂t ψ + ψ∗
= d 3 x
Hψ∗ Aψ − i A ˙ψ .
ψ∗ AHψ + ∂A
Mit den ∂t Gleichungen (2.52a,b) ergibt s
Mit den Gleichungen (2.52a,b) ergibt sich daraus
d
dt 〈A〉 = i d
〈 〉 ∂A
〈[H, A]〉 + .
dt 〈A〉 ∂t
= i 〈 〉
〉
∂A
〈[H, A]〉 + .
∂t
Dieser ändert sich mit der Zeit wie folgt:
Mit den Gleichungen (2.52a,b) ergibt sich daraus
d
dt 〈A〉 = i 〈 ∂A
〈[H, A]〉 + ∂t
. Ehrenfest Theorem (2.54)
Bemerkungen:
Bemerkungen:

Remarks:
1. H hermitian in L 2
2. Comparison to classical mechanics:
generalized momentum position coordinates p, q
equations of motion
d
dt
f (p, q, t) ={H, f } +
∂f
∂t
, {g, f } = ∂g
∂p
∂f
∂q − ∂f
∂p
∂g
∂q
Poisson bracket ⇐⇒ commutator

Examples:
[H, x i ]ψ = j
= 1
2m
= 1
2m
= 1
2m
= 1
2m
= 1
2m
p 2 j
2m x iψ − x i
p 2 j
2m ψ
p j (p j x i ψ) − x i pj 2 ψ
j
p j [(p j x i )ψ + x i p j ψ] − x i pj
2
j
j
j
j
p j
i δ ijψ + x i p j ψ
− x i p 2 j ψ
i δ ijp j ψ +(p j x i )p j ψ + x i p 2 j ψ − x i p 2 j ψ
2
δ ij p j ψ
i
= − i m p iψ =⇒ [H, x i ]=− i m p i
p j = i
∂
∂x j
[H, p i ]=[V (x), i
∂
∂x j
]=i ∂V
∂x i

insert into Ehrenfest Theorem
d
dt x = i [H, x] = 1 m p
d
dt p = i [H, p] = −∇V (x) = K(x)
where K = ∇V
=⇒ m d 2
x = K(x)
dt2 important: this is the average value
and not K(x)

Stationary Solution
assumption: H time independent ⇒ separation into
time dependent and spatially dependent part:
ψ (x, t) =f (t) ψ (x)
(strange notation)
Plugging into Schrödinger eqn.
⇒
i
i ∂ ψ (x, t) =Hψ (x, t)
∂t
∂
∂t f (t) ψ (x) =f (t) Hψ (x)
⇒
i ∂
f (t) ∂t f (t)
depends only on t
= 1 Hψ (x)
ψ (x)
depends only on x
= E (constant)
⇒ i ∂ f (t) =Ef (t) ⇒ f (t) =e−iEt/
∂t
and
Hψ (x) =Eψ (x, t)
time independent Schrödinger equation
ψ (x, t) =exp (−iEt/) ψ (x) arecalledstationarystates,
since |ψ (x, t)| 2 = |ψ (x)| 2 is time independent.

Now consider equation
Hψ (x) =Eψ (x)
This is an eigenvalue equation.
generally: ψ is an eigenfunction for the operator A with eigenvalue a, if
Aψ = aψ
We assume now that A is Hermitian.
Eigenvalues of Hermitian operators are real, since
(ψ, Aψ) =(ψ, aψ) =a(ψ, ψ)
complex conjugate equation
(Aψ, ψ) =(aψ, ψ) =a ∗ (ψ, ψ)
AHermitian⇒ (ψ, Aψ) =(Aψ, ψ) ⇒ a = a ∗
Hermitian operators must be assigned to all measurable quantities (observables)
in order that expectation values are real. H, p, x are Hermitian.