Laplace-Transformation

Mathematik 2
Teil: Laplace-Transformation ∗
Prof. Dr. Frank Seelisch
Hochschule Esslingen
Fakultät Grundlagen, Standort Göppingen
Email: frank.seelisch@hs-esslingen.de
Telefon: +49 (0)7161 670 1197
Stand: 18. September 2013
∗ Dieses Skript darf gratis gelesen, heruntergeladen, kopiert oder ausgedruckt werden. Es darf nicht
verändert oder auf wie auch immer geartete Weise bearbeitet werden. Noch darf dieses Skript auf irgendwelche
Webseiten oder Webarchive hochgeladen werden.
Die Abbildungen wurden mit der open-source-Software Geogebra erzeugt.
Die Meldung inhaltlicher Fehler und Ungereimtheiten per Mail an den Autor ist ausdrücklich erwünscht.

Inhaltsangabe
Die Laplace-Transformation erlaubt es, lineare Dierentialgleichungen höherer Ordnung,
Anfangswertprobleme, ja sogar lineare Dierentialgleichungssysteme elegant zu lösen.
Dabei wird das Ausgangsproblem in den sogenannten Frequenzbereich übersetzt,
dort gelöst und das Ergebnis dann zurücktransformiert.
Wir können auÿerdem mittels der sogenannten Übertragungsfunktion und der Faltungsoperation
auf einfache Weise den Zusammenhang zwischen Eingangs- und Ausgangssignalen
linearer Systeme untersuchen.
Inhaltsverzeichnis
1 Einführung 1
1.1 Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.1 Vor- und Nachteile . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1.2 Geeignete Problemstellungen . . . . . . . . . . . . . . . . . . . . . . 3
1.1.3 Lineare Dierentialgleichungssysteme . . . . . . . . . . . . . . . . . 3
1.1.4 Zusammenhang zwischen Eingangs- und Ausgangssignal . . . . . . 4
1.1.5 Wiederholung: Rechnen im Wechselstromkreis . . . . . . . . . . . . 5
1.2 Grundlegende Signale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2.1 Die Einheitssprungfunktion . . . . . . . . . . . . . . . . . . . . . . 7
1.2.2 Die Einheitsimpulsfunktion . . . . . . . . . . . . . . . . . . . . . . 8
1.2.3 Zusammenhang zwischen Sprung- und Impulsfunktion . . . . . . . . 9
1.2.4 Einsetzregel und Ausblendeigenschaft der DIRAC-Funktion . . . . 11
1.2.5 Verallgemeinerte Ableitungen . . . . . . . . . . . . . . . . . . . . . 11
2 Die LAPLACE-Transformation 12
2.1 Denition und erste Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.1.1 Denition der Laplace-Transformation . . . . . . . . . . . . . . . 13
2.1.2 Die Rücktransformationsformel . . . . . . . . . . . . . . . . . . . . 14
2.1.3 Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3 Wichtige Sätze zur Laplace-Transformation 15
3.1 Linearität . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.2 Dämpfung im t-Bereich, Verschiebung im s-Bereich . . . . . . . . . . . . . 15
3.3 Verschiebung im t-Bereich, Dämpfung im s-Bereich . . . . . . . . . . . . . 16
3.4 Ähnlichkeitssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
3.5 Dierentiation im t-Bereich . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.6 Dierentiation im s-Bereich . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.7 Integration im t-Bereich . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.8 Anfangs- und Endwerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
4 Die Faltung 20
4.1 Denition und Eigenschaften . . . . . . . . . . . . . . . . . . . . . . . . . . 21
4.1.1 Denition des Faltungsprodukts . . . . . . . . . . . . . . . . . . . . 21

INHALTSVERZEICHNIS 3
4.1.2 Eigenschaften der Faltung . . . . . . . . . . . . . . . . . . . . . . . 21
4.1.3 Faltung bei endlichen Träger . . . . . . . . . . . . . . . . . . . . . . 22
4.2 Der Zusammenhang von Multiplikation und Faltung . . . . . . . . . . . . . 22
5 Lösen linearer Dierentialgleichungen 23
5.1 Allgemeines Lösungsschema . . . . . . . . . . . . . . . . . . . . . . . . . . 23
5.1.1 Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
5.2 Anfangswerte für t ≠ 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
5.3 Spezielle Anregungssignale . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
5.3.1 Zusammenhang der Lösungen für die Einheitsfunktionen . . . . . . 25
6 Lösen linearer Dierentialgleichungssysteme 25
6.1 Vorgehensweise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
6.1.1 Lösung des Doppelpendelsystems . . . . . . . . . . . . . . . . . . . 26
6.1.2 Weiteres Übungsbeispiel . . . . . . . . . . . . . . . . . . . . . . . . 27
7 Die Ein-Ausgabe-Relation eines linearen Systems 28
7.1 Problemstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
7.2 Allgemeine Betrachtungen . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
7.3 Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
7.3.1 Das R − c − Glied . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

1 EINFÜHRUNG 1
1 Einführung
Die Laplace-Transformation geht zurück auf den berühmten französischen Mathematiker
Pierre-Simon Laplace, der von 1749-1827 lebte und in der Zeit nach der Französischen
Revolution sogar für einige Monate Innenminister unter Napoleon war.
1.1 Motivation
Die Laplace-Transformation ermöglicht es uns, ein gegebenes mathematisches Problem
der Regelungs- oder Elektrotechnik in eine andere mathematische Spiegelwelt zu übersetzen;
wir sagen zu transformieren. Dort kann das neue Problem dann mit weniger Aufwand
gelöst werden.
Zur Veranschaulichung der Idee der Spiegelwelt siehe die Illustration zu Lewis Carrolls
Through the Looking Glass; http://de.wikipedia.org/wiki/Datei:Tenniel,_Through_The_
Looking-Glass.gif.
Abbildung 1: Alice geht durch den Spiegel
Abbildung 2 illustriert die Hauptidee, die wir mit Hilfe der Laplace-Transformation verfolgen:
Wir möchten durch Wechsel in eine mathematische Spiegelwelt eine Problemvereinfachung
erreichen und dann das gegebene, in aller Regel schwierige Problem alternativ
lösen entlang der rot beschrifteten Pfeile. Dabei soll der eigentliche Lösungsaufwand in
der Spiegelwelt einfacher als zuvor sein.
1.1.1 Vor- und Nachteile
⊕ Die Transformation wird in aller Regel einfach zu bewerkstelligen sein. Zudem existieren
Transformationstabellen, die diesen Teil weiter vereinfachen.

1 EINFÜHRUNG 2
Abbildung 2: Alternativer Lösungsweg mittels Laplace-Transformation
⊕ Wie erwähnt ist das Lösen im s-Bereich einfach trotz des Fakts dass nun s ∈ C ist.
⊖ Die Rücktransformation ist oft nicht so einfach. Aber wie im ersten Pluspunkt bereits
erwähnt, können wir hierbei Tabellen verwenden.
Insgesamt ist zu bemerken, dass der gesamte Prozess des Lösens des Ausgangsproblems
nun sehr verschieden vom direkten Lösen ist. Denken wir z.B. an eine lineare Dierentialgleichung
höherer Ordnung mit konstanten Koezienten: Beim ursprünglichen Lösungsverfahren
sucht verfährt man in mehreren Schritten;
1. Lösen des charakteristischen Polynoms,
2. Fundamentallösungen bzw. homogene Lösung y hom ,
3. Störgliedansatz zum Aunden einer Partikulärlösung y p (dabei auf Resonanz achten!),
4. Gesamtlösung als Summe von y hom und y p .
Der neue Rechenweg über die Laplace-Transformation sieht dagegen komplett anders
aus. Allerdings tritt auch hier - und zwar ganz automatisch - das charakteristische Polynom
in Erscheinung. Wir müssen aber bei diesem Weg nicht mehr auf Resonanz achten:

1 EINFÜHRUNG 3
Die Laplace-Transformation beachtet diesen Sonderfall ganz automatisch selbst und
nimmt uns hier etwas Denkarbeit ab.
1.1.2 Geeignete Problemstellungen
Welche mathematischen Problemstellungen könen wir nun tatsächlich geschickt mit Hilfe
der Laplace-Transformation lösen?
Typische Anwendungsszenarien bieten die folgenden Aufgabenstellungen:
• gewöhnliche lineare Dierentialgleichungen höherer Ordnung mit konstanten Koezienten
(Wie oben erwähnt, muss dabei nicht mehr auf Resonanz geachtet werden.),
• Anfangswertprobleme (Die Anfangswerte gehen dabei direkt während der Übersetzung,
d.h. der Transformation des Ausgangsproblem ein.),
• lineare Dierentialgleichungssysteme mit konstanten Koezienten und schlieÿlich
die
• Untersuchung des Zusammenhangs zwischen Eingangs- und Ausgangssignal bei elektrischen
Elementen wie z.B. dem R − c − Glied.
Bevor wir beginnen, uns die eigentliche Transformation anzuschauen und gegebene Probleme
tatsächlich zu lösen, werfen wir einen Blick auf die letzten beiden Aufgabenstellungen,
um zu verstehen, worum es dabei geht.
1.1.3 Lineare Dierentialgleichungssysteme
Ein einfaches Beispiel für ein lineares Dierentialgleichungssystem mit konstanten Koef-
zienten ergibt sich aus der Betrachtung des Doppelpendels, siehe Abbildung 3.
Dabei werden zwei normale Fadenpendel (I) und (II) über eine Feder miteinander gekoppelt.
Weiterhin nehmen wir der Einfachheit halber an, dass beide Pendel die selbe
Fadenlänge l und Masse m besitzen und dass die Auslenkungswinkel α und β klein sind,
d.h. nicht gröÿer als 10 ◦ .
Wir machen für jedes Pendel den Kraftansatz
Gesamtkraft = Reibkraft + Gewicht + Federkraft
und erhalten die beiden Dierentialgleichungen
(I) m · l · α ..
= −ν · l · α .
− m · g · α − k · l · (α − β),
(II) m · l · β ..
= −ν · l · β .
− m · g · β − k · l · (β − α).
Dabei ist k die Federkonstante, g die Fallbeschleunigung und ν der Reibkoezient, wobei
wir von sogenannter Stokesscher Reibung ausgehen, d.h. von einer Reibkraft, die sich
proportional zur Geschwindigkeit verhält.
Man sieht, dass beide gesuchten Funktionen, nämlich die Zeit-abhängigen Auslenkungswinkel
α(t) und β(t), in beiden Dierentialgleichungen vorkommen. Dadurch wird das

1 EINFÜHRUNG 4
Abbildung 3: Zwei normale, über eine Feder gekoppelte Fadenpendel
Problem zu einem sogenannten Dierentialgleichungssystem. Wir können hier nicht mehr
einfach eine Gleichung verwenden, um eine Unbekannte zu bestimmen.
Wir werden später sehen, dass das transformierte Problem ein lineares Gleichungssystem
mit zwei Gleichungen und zwei Unbekannten und somit leicht zu lösen ist.
1.1.4 Zusammenhang zwischen Eingangs- und Ausgangssignal
Um auch diese Aufgabenstellung kurz zu erklären, betrachten wir ein sogenanntes R −
c − Glied im Wechselstromkreis; siehe Abbildung 4.
Abbildung 4: R − c − Glied im Wechselstromkreis
Wir können die über der gesamten Strecke angelegte Spannung u in als Eingangssignal
des R − c − Glieds betrachten. Dann stellt sich über dem Kondensator ein bestimmtes

1 EINFÜHRUNG 5
Ausgangssignal u out ein.
Wir werden sehen, dass wir mit Hilfe der Laplace-Transformation den Zusammenhang
zwischen diesen beiden Signalen einfach studieren und verstehen können. So ergibt sich
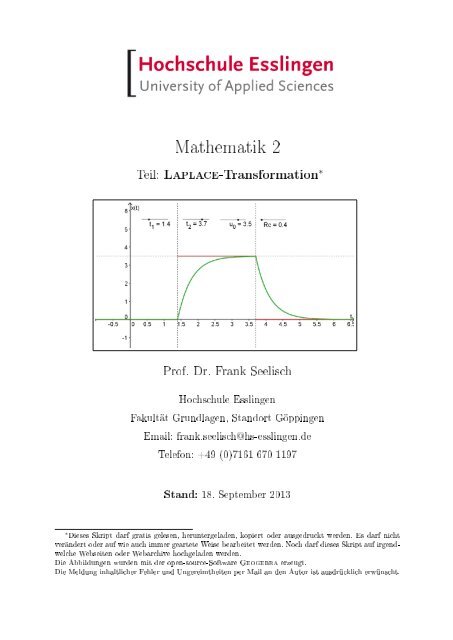
im Fall einer Rechteck-förmigen Eingangsspannung u 0 , die zwischen den Zeitpunkten t 1
und t 2 angelegt wird, eine Ausgangsspannung wie in Abbildung 5 in grün dargestellt. Die
grüne Kurve ist dabei noch abhängig vom Produkt des Ohmschen Widerstands R und
der Kapazität c.
Abbildung 5: Rechteck-förmiges Eingangssignal und resultierendes Ausgangssignal
1.1.5 Wiederholung: Rechnen im Wechselstromkreis
Dieser Abschnitt ist reine Wiederholung und illustriert noch einmal, dass für das Rechnen
im Wechselstromkreis die komplexen Zahlen C gut geeignet sind.
Es ist daher nicht verwunderlich, wenn wir im s-Bereich mit einer komplexwertigen Variablen
s rechnen (, auch wenn wir dies nur selten beim Rechnen beachten müssen oder
überhaupt merken werden).
Zur Wiederholung betrachten wir einen Ohmschen Widerstand und - dieses Mal dazu
parallel geschaltet - einen Kondensator; siehe Abbildung 6.
Es sei die Wechselspannung
u(t) = A · cos (ωt)
an die Schaltung angelegt. Wir suchen den resultierenden Stromverlauf i(t).
Lösung:
1. Schritt: Wir übersetzen u(t) und das gesuchte i(t) in komplexe Gröÿen:
u C (t) := A · e jωt ,
i C (t) gesucht.

1 EINFÜHRUNG 6
Abbildung 6: Ohmscher Widerstand und Kondensator parallel geschaltet
Die komplexen Zahlen C spielen hier also die Rolle der Spiegelwelt. (Dies ist aber nicht
die Spiegelwelt, in der wir uns bei der Laplace-Transformation bewegen werden.) Dann
gelten die Rücktransformationsregeln
u(t) = Re (u C (t)) und i(t) = Re (i C (t)) .
2. Schritt: Nun müssen wir die realen Wiederstände in komplexe Widerstände, die sogenannten
Impendanzen übertragen: Statt R und c haben wir nun z R und z c mit folgenden
Formeln:
z R = R, z c = 1
jcω .
3. Schritt: Wir berechnen nun die Gesamtimpedanz. Dabei verwenden wir das Gesetz für
die Parallelschaltung von Wiederständen, die auch für Impedanzen gilt, d.h.
1
= 1 + 1 = 1 z ges z R z c R + jcω
4. Schritt: Jetzt können wir mit Hilfe des Ohmschen Gesetzes für Impedanzen
den Strom berechnen:
i C = u C
z ges
=
z = u C
i C
( )
( )
1 A
R + jcω · A · e jωt =
R + j · cωA · e jωt .
Es fällt auf, dass die Klammer gar nicht von der Zeit t, sondern nur von unseren Ausgangsparametern
A, R, c und ω abhängt. Somit ist auch der Strom i C (t) eine Kreisschwingung
mit der gleichen Kreisfrequenz ω also analog zu u C (t). Lediglich die Anfangszeiger
sind unterschiedlich, nämlich für die Spannung gleich A und für den Strom gleich
( A
R + j · cωA) ; siehe Abbildung 7.

1 EINFÜHRUNG 7
5. Schritt: Um i(t) zu berechnen, empehlt es sich, den Anfangszeiger von i C (t) in Exponentialdarstellung
zu bringen:
A
R + j · cωA =: r · ejφ ,
wobei r = A √ 1/R 2 + c 2 und φ = arctan(cωA/(A/R)) = arctan(cωR). Dann folgt
i C (t) = r · e j(ωt+φ) bzw. i(t) = Re(i C (t)) = r · cos (ωt + φ).
Abbildung 7: Anfangszeiger von Spannung (rot) und Strom (grün)
1.2 Grundlegende Signale
1.2.1 Die Einheitssprungfunktion
Denition 1 (Sprung- oder HEAVISIDE-Funktion)
Die Funktion
σ : R \ {0} → {0, 1}
{ 0, t < 0,
t ↦→
1, t > 0
heiÿt Einheitssprungfunktion oder kurz Sprungfunktion oder HEAVISIDE-
Funktion.
Oliver Heaviside war ein britischer Mathematiker und Physiker und lebte von 1850-1925.
Diese Funktion ist also an der Stelle t = 0 gar nicht deniert. Wir werden sehen, dass in
der Theorie der Laplace-Transformation einzelne Funktionswerte keine Rolle spielen, da
es immer um den zeitlichen Verlauf von Signalen geht. Und für diese ist es nicht wichtig,

1 EINFÜHRUNG 8
was zu einem ganz bestimmten Zeitpunkt passiert. Insofern ist es nur konsequent, dass
wir σ(t) für t = 0 gar nicht denieren.
Die HEAVISIDE-Funktion modelliert also den Wechsel vom Nullniveau auf ein bestimmtes
Nichtnullniveau. Und klar; wenn wir σ(t) mit einer Konstante multiplizieren, können
wir jeden Wert für t > 0 erzwingen.
Für a > 0 ist σ(t − a) natürlich die um a nach rechts verschobene Sprungfunktion; siehe
Abbildung 8 für einige einfache Beispiele.
Abbildung 8: Einige einfache Sprungfunktionen
Durch Kombination mehrerer Terme der Form a · σ(t − b) können wir beliebige Treppenfunktionen
zusammenbauen.
Beispiel 1
a) σ(t − a) − σ(t − b) für beliebige a, b ∈ R mit 0 < a < b
b) 3σ(t) + 2σ(t − 2) − 4σ(t − 3)
c) (1 − t) · (σ(t + 1) − σ(t)) + t · (σ(t) − σ(t − 1))
1.2.2 Die Einheitsimpulsfunktion
Wir betrachten die Funktionenschar
r a (t) := 1 (σ(t) − σ(t − a)) ,
a
für a > 0.
Abbildung 9 zeigt einen typischen Vertreter mit Nichtnullniveau 1/a und einer Intervalllänge
a, auf der die Nichtnullwerte angenommen werden. Es folgt also direkt für die Fläche
unter dem Rechtecksignal r a :
∫ ∞
−∞
r a (t) dt = 1.

1 EINFÜHRUNG 9
Abbildung 9: Rechteckfunktion r a (t) mit konstanter Fläche 1
Nun lassen wir a gegen 0 + gehen und erhalten die Einheitsimpulsfunktion
{ ∞, t = 0,
δ(t) :=
0, t ≠ 0 ,
wobei das ∞ so gewählt wird, dass die Fläche immernoch 1 ergibt, d.h.
∫ ∞
−∞
δ(t) dt = 1.
Achtung! Die hier gegebene Herleitung bzw. Denition der Einheitsimpulsfunktion ist
mathematisch nicht korrekt, schon allein, weil ∞ kein zulässiger Funktionswert ist. Eine
korrekte Herleitung bedarf Vorwissen aus anderen mathematischen Disziplinen, auf das
wir hier nicht näher eingehen wollen.
Die Einheitsimpulsfunktion wird auch kurz als Impulsfunktion oder - zu Ehren von
Paul Dirac, einem englischen Quantenphysiker und Nobelpreisträger (1902-1984) - als
DIRAC-Funktion bezeichnet. Daher rührt auch die Bezeichnung delta.
Man stellt sich die DIRAC-Funktion am besten als einen zeitlich sehr kurzen Impuls
von sehr groÿer Amplitute vor, d.h. als r a (t) mit sehr kleinem a > 0. Um das Schaubild
von δ(t) in einem Koordinatensystem darzustellen wird ein Vektorpfeil verwendet. Auch
hier können wir die Amplitude wieder vervielfachen oder den Zeitpunkt des Impulses
verschieben sowie Linearkombinationen bilden; siehe Abbildung 10.
1.2.3 Zusammenhang zwischen Sprung- und Impulsfunktion
Wir denieren die Rampenfunktion
⎧
⎨ 0, t < 0,
m a (t) := t/a, 0 ≤ t ≤ a,
⎩
1, t > a
,

1 EINFÜHRUNG 10
Abbildung 10: Diracfunktion und Modikationen
wiederum für beliebiges a > 0; siehe Abbildung 11.
Dann ist m a (t) für alle t ≠ 0 und t ≠ a dierenzierbar mit der Ableitung
Abbildung 11: Rampenfunktion m a (t)
m ′ a(t) :=
{ 0, t < 0 und t > a,
1/a, 0 ≤ t ≤ a.
Indem wir das Verhalten an einzelnen Zeitpunkten ignorieren, können wir also kurz sagen
m ′ a(t) = r a (t).
Wir hatten ja oben schon gesehen, dass r a (t) → δ(t) für a → 0 + . Analog stellen wir fest,
dass m a (t) → σ(t) für a → 0 + . Zusammen ergibt sich also - wiederum hier mathematisch
nicht ganz korrekt ausgeführt -
d
σ(t) = δ(t) .
dt
Mit anderen Worten:

1 EINFÜHRUNG 11
MERKE: Zusammenhang zwischen δ und σ
1. Die DIRAC-Funktion kann als die Ableitung der HEAVISIDE-Funktion betrachtet
werden.
1.2.4 Einsetzregel und Ausblendeigenschaft der DIRAC-Funktion
Satz 1 (Einsetzregel für δ)
Sei f(t) stetig an der Stelle t 0 ∈ R. Dann gilt die Einsetzformel
f(t) · δ(t − t 0 ) = f(t 0 ) · δ(t − t 0 ) .
Als direkte Folgerung ergibt sich die Integralformel
∫ ∞
f(t) · δ(t − t 0 ) dt =
∫ ∞
f(t 0 ) · δ(t − t 0 ) dt = f(t 0 ) ·
∫ ∞
δ(t − t 0 ) dt = f(t 0 ),
−∞
−∞
−∞
die auch als Ausblendeigenschaft der DIRAC-Funktion bezeichnet wird.
1.2.5 Verallgemeinerte Ableitungen
Aufgrund der Beziehung d/dtσ(t) = δ(t) sind wir schon fast in der Lage, beliebige abschnittsweise
denierte Funktionen zu dierenzieren. Da solche Funktionen aufgrund von
Sprüngen und Knicken nicht im eigentlichen Sinne dierenzierbar sind, sprechen wir im
Folgenden von der verallgemeinerten Ableitung.
Nehmen wir an, wie möchten die abschnittweise denierte Funktion
s(t) = (2 + t) · σ(t − 1)
ableiten. Wir kennen zwar die (verallgemeinerten) Ableitungen jedes Faktors, doch was
machen wir mit dem Produkt? Hier gilt zum Glück auch weiterhin die Produktregel:
Satz 2 (Verallgemeinerte Produktregel)
Bei Ableiten von Termen der Form f(t) · σ(t − t 0 ), wobei f dierenzierbar ist, gilt die
verallgemeinerte Produktregel
d
dt [f(t) · σ(t − t 0)] = f ′ (t) · σ(t − t 0 ) + f(t 0 ) · δ(t − t 0 ) .
Dabei würde man im letzten Term zwar den Vorfaktor f(t) erwarten. Diesen können wir
aber gemäÿ Satz 1 sofort durch f(t 0 ) ersetzen.

2 DIE LAPLACE-TRANSFORMATION 12
Damit können wir nun s ′ (t) berechnen:
s ′ (t) = 1 · σ(t − 1) + (2 + t) · δ(t − 1) = σ(t − 1) + 3 · δ(t − 1) .
(Hierbei haben wir die Einsetzregel mit t 0 = 1 angewendet.)
Abbildung 12 zeigt s(t) und die verallgemeinerte Ableitung s ′ (t).
Nach diesem Beispiel ist relativ klar wie man, ausgehend vom Schaubild einer abschnitts-
Abbildung 12: s(t) und seine verallgemeinerte Ableitung s ′ (t)
weise denierten Funktion, direkt deren verallgemeinerte Ableitung skizziert ohne diese
zu berechnen:
MERKE: Verallgemeinertes Ableiten grasch
1. Dort, wo die Ausgangsfunktion dierenzierbar ist, leitet man ganz normal ab.
2. Eine Sprungstelle t s der Höhe h s schlägt sich in der Ableitung in dem Term h s ·
δ(t − t s ) nieder.
Beispiel 2 Skizzieren Sie jeweils die gegebene Funktion und danach sofort (d.h. ohne
Rechnung) deren verallgemeinerte Ableitung.
Berechnen Sie dann die verallgemeinerte Ableitung mit Hilfe von Satz 2 und vergleichen
Sie ihr Ergebnis mit dem zuvor angefertigten Schaubild.
a) (1 + t) · (σ(t + 1) − σ(t)) + (1 − t) · (σ(t) − σ(t − 1))
b) 2 − 2σ(t − 2) + (t − 3) 2 · (σ(t − 2) − σ(t − 4)) + σ(t − 4)
2 Die LAPLACE-Transformation
Genau wie auch die FOURIER-Transformation handelt es sich bei der LAPLACE-
Transformation um eine sogenannte Integraltransformation, da - wie wir gleich sehen

2 DIE LAPLACE-TRANSFORMATION 13
werden - der Wechsel in die Spiegelwelt mathematisch durch eine Integralformel bewerkstelligt
wird.
Wie schon am Anfang erläutert werden wir die LAPLACE-Transformation für die Untersuchung
physikalisch-technischer Systeme verwenden. Da wir diese immer erst ab einem
bestimmten Zeitpunkt untersuchen, beschränken wir uns für die zeitlichen Verläufe ab
einem t ≥ t 0 . Ohne Einschränkung können wir dabei t 0 = 0 annehmen.
2.1 Denition und erste Beispiele
2.1.1 Denition der Laplace-Transformation
Denition 2 (Laplace-Transformation)
Sei f(t) eine beliebige, für t ≥ 0 denierte Funktion. Dann heiÿt die komplexwertige
Funktion
F (s) :=
∫ ∞
0
f(t) e −st dt
die Laplace-Transformierte zu/von f und zwar für all jene s ∈ C, für die das
Integral existiert. Wir schreiben dann
f(t) ◦ • F (s) oder F (s) = L{f(t)};
lies: klein f von t transformiert zu groÿ F von s bzw. groÿ F von s ist die Transformierte
von klein f von t.
In der Denition tritt also ein uneigentliches Integral mit komplexwertigem Integranden
auf.
Wiederholung aus Mathe 1:
∫ ∞
0
. . . dt = lim
b→∞
∫b
0
. . . dt.
Aber wie ist ein Integral mit komplexwertigem Integranden zu verstehen? Ganz einfach:
∫ b
0
f(t) e −st dt
s=x+jy
=
=
=
∫ b
0
∫ b
f(t) e −xt e −jyt dt
f(t) e −xt · (cos (−yt) + j sin (−yt)) dt
0
∫ b
∫ b
f(t) e −xt cos (yt) dt − j · f(t) e −xt sin (yt) dt;
0
0

2 DIE LAPLACE-TRANSFORMATION 14
also eine aus zwei herkömmlichen Integralen gebildete komplexe Zahl.
Man sieht auch, dass der Faktor e −xt = e −Re(s)t für Re(s) > 0 für die Konvergenz des
uneigentlichen Integrals sorgt (, falls nicht f(t) zu stark wächst für t → ∞).
2.1.2 Die Rücktransformationsformel
Satz 3 (Laplace-Rücktransformation)
Sei f(t) ◦ • F (s) eine Laplace-Transformation. Dann gilt
f(t) = 1
2πj ·
∫
s=x+j∞
s=x−j∞
F (s) e st ds,
wobei x beliebig gewählt werden kann, allerdings groÿ genug, so dass F (x + jy) für alle
y ∈ R deniert ist.
Für die Rückrichtung der Transformation schreiben wir F (s) • ◦ f(t).
Die Schreibweise ist also nur die gespiegelte Version der in Denition 2 eingeführten
Schreibweise.
Die Integration verläuft entlang eines Integrationspfads in C, genauer entlang einer Geraden
mit konstantem Realteil x, so dass F (s) für jedes s auf dieser Geraden deniert
(sprich: das Integral aus Denition 2 konvergent) ist.
Glücklicherweise brauchen wir an dieser Stelle nicht näher auf die Integration in C einzugehen;
damit beschäftigt sich die mathematische Disziplin der Funktionentheorie. Stattdessen
werden wir einige aus dem Reellen bekannte Rechenregeln übernehmen und damit
ausreichend gut rechnen können. Zudem gibt es umfangreiche Transformationstabellen, in
denen die wichtigsten Transformationspaare f(t)◦ •F (s) nachgeschlagen werden können.
2.1.3 Beispiele
Zur Übung wollen wir trotzdem einige einfache Transformationspaare manuell berechnen;
nicht zuletzt, um das Rechnen mit komplexen Integralen zu üben bzw. um zu sehen, dass
man dazu nur reell integrieren können muss.
Beispiel 3 Man berechne die Laplace-Transformierten der folgenden Funktionen
unter alleiniger Verwendung von Denition 2:
a) f(t) = σ(t),
b) f(t) = σ(t − a) , a > 0,
c) f(t) = A · (σ(t − t 1 ) − σ(t − t 2 )) , 0 < t 1 < t 2 ; A ∈ R
d) f(t) = σ(t) · cos (ωt),
e) f(t) = e at , a ∈ C

3 WICHTIGE SÄTZE ZUR LAPLACE-TRANSFORMATION 15
f) f(t) = σ(t) · t n , n ∈ N +
3 Wichtige Sätze zur Laplace-Transformation
Die in diesem Abschnitt aufgeführten Sätze sollen uns befähigen, möglichst viele Funktionen
aus dem Zeitbereich in den Frequenzbereich transformieren zu können. Das Muster ist
dabei immer das selbe: Angenommen man kennt schon ein oder mehrere gültige Transformationspaare
(z.B. aus einer Tabelle), wie kann man sich dann daraus neue gültige Paare
basteln?
Da die meisten Beweise relativ einfach sind, geben wir diese mit an; auch um damit
die verschiedenen Schreibweisen im Zusammenhang mit der Laplace-Transformation zu
üben.
3.1 Linearität
Satz 4 (Linearität)
Aus den Transformationen f ◦ • F, g ◦ • G folgt af + bg ◦ • aF + bG für alle a, b ∈ R.
Für b = 0 kann man das auch so lesen: Man darf die Transformation f ◦ • F auf beiden
Seiten mit einer Zahl a durchmultiplizieren.
Und für a = b = 1 steht dort, dass man die linken und rechten Seiten zweier gegebener
Transformationen einfach addieren darf.
Beweis: Grund für die Richtigkeit der Linearität der Laplace-Transformation ist die
Linearität der Integration:
∫ ∞
(af(t) + bg(t)) e −st dt = a
∫ ∞
f(t)e −st dt + b
∫ ∞
g(t)e −st dt,
0
d.h. L{af + bg} = aL{f} + bL{g}.
Beispiel 4
0
0
a) e jωt ◦ • . . .
e −jωt ◦ • . . .
=⇒ cos (ωt) ◦ • . . . , sin (ωt) ◦ • . . .
•
1
s 2 +3s+2 • ◦ . . .
3.2 Dämpfung im t-Bereich, Verschiebung im s-Bereich
Satz 5 (t-Dämpfung, s-Verschiebung)
Aus der Transformation f ◦ • F folgt e at · f(t) ◦ • F (s − a) für alle a ∈ C.

3 WICHTIGE SÄTZE ZUR LAPLACE-TRANSFORMATION 16
Beweis:
∫ ∞
∫ ∞
F (s − a) = f(t)e −(s−a) dt = e at f(t)e −st dt = L{e at f(t)}
Beispiel 5
0
0
a) e at · σ(t) ◦ • . . .
b) e −at sin (ωt)
c)
5s+1
s 2 +2s+5 • ◦ . . .
3.3 Verschiebung im t-Bereich, Dämpfung im s-Bereich
Satz 6 (t-Verschiebung, s-Dämpfung)
Aus der Transformation f ◦ • F folgt σ(t − a) · f(t − a) ◦ • e −as · F (s) für alle a ∈ C.
Beweis:
∫ ∞
σ(t − a) f(t − a)e −st dt =
∫ ∞
f(t − a)e −st dt
0
a
∫ ∞
Subst.: ˜t = t − a = f(˜t)e −s(˜t+a) d˜t
0
∫ ∞
= e −sa · f(˜t)e −s˜t d˜t = e −sa L{f}.
Beispiel 6
a) σ(t − a) ◦ • . . .
b) 1−e−3s
s+2
• ◦ . . .
0
3.4 Ähnlichkeitssatz
Satz 7 (Ähnlichkeitssatz)
Aus der Transformation f ◦ • F folgt f(at) ◦ • 1/a · F (s/a) für alle a > 0.

3 WICHTIGE SÄTZE ZUR LAPLACE-TRANSFORMATION 17
Ersetzt man a durch 1/b, so ergibt sich eine andere gebräuchliche Darstellung dieses Satzes:
( t
f ◦ • F =⇒ f ◦ • b · F (bs).
b)
Beweis:
L{f(at)} =
∫ ∞
f(at)e −st dt
Beispiel 7
Subst.: ˜t = at =
0
∫ ∞
0
f(˜t)e − s ˜t d˜t
a
a = 1 ( s
)
a · F .
a
a) sin t ◦ • 1
s 2 +1
=⇒ sin (ωt) ◦ • . . .
b) e t + te t ◦ • . . . =⇒ (1 + at)e at ◦ • . . .
3.5 Dierentiation im t-Bereich
Satz 8 (t-Dierentiation)
Gegeben sei die Transformation f ◦ • F . Für Re(s) > 0 gelten dann ebenfalls die
Transformationen
f ′ (t) ◦ • s · F (s) − f(0)
f ′′ (t) ◦ • s 2 · F (s) − s · f(0) − f ′ (0)
.
f (k) (t) ◦ • s · L{f (k−1) (t)} − f (k−1) (0).
Expandiert man die letzte Zeile, so ergibt sich
f (k) (t) ◦ • s k · F (s) − s k−1 · f(0) − s k−2 · f ′ (0) − . . . − s 1 · f (k−2) (0) − f (k−1) (0).
Man überlegt sich, dass nur die Formel für f ′ (t) zu beweisen ist, denn f ′′ (t) ist die erste
Ableitung von f ′ (t), d.h. alle anderen Formeln folgen dann durch wiederholte Anwendung
der Formel für die erste Ableitung.
Beweis: Für den Fall f ′ (t) resultiert der Beweis aus einer Anwendung der partiellen
Integration:
L{f ′ (t)} =
∫ ∞
f ′ (t)e −st dt
0

3 WICHTIGE SÄTZE ZUR LAPLACE-TRANSFORMATION 18
part. Int. mit u ′ = f ′ , v = e −st = [ f(t)e −st] ∞
∫
0 − ∞
= 0 − f(0) + s ·
0
∫ ∞
0
f(t)(−s)e −st dt
f(t)e −st dt.
Dieser Satz ist wichtig für die Transformation von Dierentialgleichungen und Dierentialgleichungssystemen,
da dort ja Ableitungen auftreten.
Beispiel 8
a) f(t) := sin (ωt) ◦ •
ω
s 2 +ω 2
=⇒ f ′ (t) ◦ • . . . =⇒ cos (ωt) ◦ • . . .
3.6 Dierentiation im s-Bereich
Satz 9 (s-Dierentiation)
Gegeben ist die Transformation f ◦ •F . Dann folgt die Transformation −t·f(t)◦ •F ′ (s).
Beweis: Dierenziert man die Transformationsgleichung F (s) = ∫ ∞
0
f(t)e −st dt auf beiden
Seiten nach s, so ergibt sich
F ′ (s) = d ds
∫ ∞
f(t)e −st dt
=
0
∫ ∞
∫ ∞
f(t) d ds e−st dt = −t · f(t)e −st dt
0
= L{−t · f(t)},
0
wobei wir nicht näher auf die (an dieser Stelle zulässige) Vertauschung von Dierentiation
und Integration (von der ersten zur zweiten Zeile) eingehen.
Beispiel 9
a) f(t) = 1 ◦ • 1, d.h. 1 • ◦ 1
s s
=⇒ dn 1
• ◦ . . .
ds n s
b) sin t ◦ • 1
1+s 2
=⇒ d 1
ds
1+s 2 • ◦ . . .

3 WICHTIGE SÄTZE ZUR LAPLACE-TRANSFORMATION 19
3.7 Integration im t-Bereich
Satz 10 (t-Integration)
Gegeben sei wieder die Transformation f(t) ◦ • F (s). Dann folgt
∫ t
0
f(u) du ◦ • F (s)
s .
Aus ∫ Mathematik 1 ist bekannt, dass das von seiner oberen Grenze t abhängige Integral
t
f(u) du nichts weiter als eine Stammfunktion von f(t) ist (, wenn f(t) stückweise stetig
0
ist). Unter all den Stammfunktionen von f(t) ist es darüber hinaus diejenige Stammfunktion,
die an der Stelle t = 0 den Wert Null hat, d.h. deren Schaubild durch den Ursprung
verläuft.
Beweis: Sei also die durch den Ursprung verlaufende Stammfunktion von f(t) mit G(t)
bezeichnet. Dann gilt
part. Int.: f = u ′ , e−st
s
F (s)
s
=
= v =
∫ ∞
0
f(t) e−st
s
[G(t) · e−st
= 0 − 0 +
s
∫ ∞
dt
] ∞
t=0
−
∫ ∞
0
G(t)e −st dt,
G(t) ( − −st) dt
0
wobei wir noch angenommen haben, dass lim t→∞ G(t)e −st
Re(s) > 0 erfordert.
= 0 ist, was auf jeden Fall
Beispiel 10
a) f(t) = 1 ◦ • 1 s
=⇒ t ◦ • . . .
b) 1 2 t sin t ◦ • s
(s 2 +1) 2
=⇒
1
(s 2 +1) 2 • ◦ 1 2
∫ t
0
x sin x dx = . . .

4 DIE FALTUNG 20
3.8 Anfangs- und Endwerte
Satz 11 (Anfangs- und Endwerte)
Aus der Transformation f(t)◦ •F (s) folgen nachstehende Formeln für f(0 + ) und f(∞):
lim f(t) = lim
t→0 +
lim
t→∞
s · F (s)
s→∞
f(t) = lim s→0 +
und
Der Grenzübergang s → ∞ bedeutet dabei genauer Re(s) → ∞, d.h. es ist egal wie sich
der Imaginärteil von s während des Grenzübergangs verhält.
Achtung! Die zweiten Ausage gilt im Allgemeinen nur, wenn F (s) in der rechten Halbebene
{s ∈ C | Re(s) ≥ 0} höchstens einen einfachen Pol an der Stelle s = 0 besitzt.
Wir verzichten an dieser Stelle auf den Beweis des Satzes.
Beispiel 11
a) σ(t) ◦ • 1 und 1/s besitzt nur einen Pol erster Ordnung bei s = 0. Demnach gelten
s
beide Formeln, nämlich:
. . .
b) F (s) = s • ◦ t sin t = f(t)
(s 2 +1) 2 2
lim t→0 + f(t) = . . . ...
lim t→∞ f(t) = . . . ???
c) Wir suchen die Rücktransformation f(t) von 1 • ◦ f(t).
F (s) = 1 hat keine Pole, d.h. beide Formeln gelten:
=⇒ . . . =⇒ f(t) = δ(t)
4 Die Faltung
Wir haben nun zahlreiche Hilfsmittel beisammen, um aus gegebenen, z.B. tabellierten
oder bereits berechneten Transformationspaaren weitere korrekte Transformationspaaare
zu berechnen.
Nun soll uns die Frage beschäftigen, wie wir aus den gegebenen Transformierten von f(t)
und g(t) die Transformierte von f(t)·g(t) erzeugen können. Dies erönet uns dann weitere
Rechenwege, um Transformationen zu bewerkstelligen.
Zudem wird uns die Antwort auf diese Frage sehr weiterhelfen beim Verständnis der Ein-
Ausgabe-Relation eines linearen Systems, das wir weiter unten behandeln.

4 DIE FALTUNG 21
4.1 Denition und Eigenschaften
4.1.1 Denition des Faltungsprodukts
Denition 3 (Faltungsprodukt/Faltung)
Seien f und g zwei reell-wertige, auf ganz R denierte Funktionen. Dann nennt man
die für jedes x ∈ R durch das uneigentliche Integral
f ∗ g (x) :=
∫ ∞
f(u) · g(x − u) du
denierte Funktion Faltung oder Faltungsprodukt von f und g.
−∞
Das Ergebnis der Faltungsoperation ist also wieder eine auf ganz R denierte reell-wertige
Funktion, deren jeder Funktionswert durch ein Integral berechnet werden muss.
Die Denition ist natürlich nur dann sinnvoll, wenn das Integral auch für jeden x-Wert
existiert, d.h. eine reelle Zahl ergibt.
Beispiel 12 f(x) = σ(x) e x , g(x) = e 2x
=⇒ f ∗ g (x) = . . ..
4.1.2 Eigenschaften der Faltung
Satz 12 (Faltungseigenschaften)
Für die Funktionen f, g, h und c ∈ R gelten:
(1) f ∗ g = g ∗ f (* ist kommutativ)
(2) f ∗ (g + h) = f ∗ g + f ∗ h (* ist distributiv)
(3) (f ∗ g) ∗ h = f ∗ (g ∗ h) (* ist assoziativ)
(4) (cf) ∗ g = c(f ∗ g) = f ∗ (cg) (Skalare sind verschiebbar)
(5) f ∗ δ = f (δ ist neutrales Element)
Bis auf (3) und (4) sind das einfache Folgerung aus der Integralrechnung, z.B. die Kommutativität:
∫ ∞
f(u) · g(x − u) du ũ:=x−u
=
∫
−∞
f(x − ũ) · g(ũ) (−dũ) =
∫ ∞
g(ũ) · f(x − ũ) dũ.
−∞
∞
−∞

4 DIE FALTUNG 22
4.1.3 Faltung bei endlichen Träger
Ist eine Funktion nur auf einem endlichen Intervall ungleich Null, so sagt man sie besitzt
einen endlichen Träger; genauer:
Denition 4 (Träger einer Funktion)
Zu einer Funktion f(x), x ∈ R heiÿt die Menge
Träger von f.
f(t) = σ(t + 1) − σ(t − 2) besitzt den Träger [−1, 2]; also endlichen Trä-
Beispiel 13
ger.
T f := {x ∈ D f | f(x) ≠ 0}
Falls f und g beide endlichen Träger haben, so hat auch f ∗ g wieder endlichen Träger,
denn mit T f = [a, b] und T g = [c, d] folgt:
∫ ∞
f(u) · g(x − u) du =
∫ b
f(u) · g(x − u) du = 0,
−∞
a
falls x − b > d ist oder x − a < c. (Man mache sich klar, dass x − u ∈ [x − b, x − a].)
Damit muss der Träger von f ∗ g enthalten sein in [a + c, b + d].
4.2 Der Zusammenhang von Multiplikation und Faltung
Satz 13 (Faltungssatz)
Multiplikation im Zeitbereich ist Faltung im Frequenzbereich;
Multiplikation im Frequenzbereich ist Faltung im Zeitbereich.
D.h. aus f(t) ◦ • F (s) und g(t) ◦ • G(s) folgen die Transformationspaare
Beispiel 14
f(t) · g(t) ◦ • F (s) ∗ G(s), und f(t) ∗ g(t) ◦ • F (s) · G(s)
a) f(t) = g(t) = σ(t) =⇒ F (s) = G(s) = 1 s
−→ 1 s 2 ◦ • . . .
b) H(s) =
1
s 2 +7s+6 = 1
s+1 · 1
s+6 • ◦ . . .

5 LÖSEN LINEARER DIFFERENTIALGLEICHUNGEN 23
5 Lösen linearer Dierentialgleichungen mittels Laplace-
Transformation
Wir betrachten (gewöhnliche) lineare Dierentialgleichungen höherer Ordnung mit konstanten
Koezienten; genauer entsprechende Anfangswertprobleme mit Anfangsbedingungen
zum Zeitpunkt t = 0.
Für diese haben wir schon ein Lösungsverfahren kennengelernt. Es zeigt sich, dass diese
Problemklasse auch sehr gut mit Hilfe der LAPLACE-Transformation gelöst werden
kann.
5.1 Allgemeines Lösungsschema
Gegeben ist also ein Anfangswertproblem der Ordnung n ≥ 2 wie soeben beschrieben:
a n · y (n) (t) + . . . a 1 · y ′ (t) + a 0 · y(t) = r(t),
y(0) = c 0 , y ′ (0) = c 1 , . . . , y (n−1) (0) = c n−1 ,
wobei die Koezienten a k und die Werte c k vorgegebene reelle Zahlen sind.
METHODE: Lösungsschema für lin. DGLen
1. Transformation des AWPs (siehe Satz 8)
2. Auösen der resultierenden Gleichung nach Y (s)
3. Rücktransformation = Lösung des AWPs
Schauen wir uns dies einmal auf dem allgemeinen Level an:
y(t) ◦ • Y (S) kurz: Y
y ′ (t) ◦ • s · Y (s) − y(0) = s 1 · Y − c 0
y ′′ (t) ◦ • s 2 · Y (s) − s 1 · y(0) − y ′ (0) = s 2 · Y − s · c 0 − c 1
.
y (n) (t) ◦ • s n · Y (s) − s n−1 · y(0) − . . . − y (n−1) (0) = s n · Y − s n−1 · c 0 − . . . − c n−1
Wir multiplizieren die erste Zeile mit a 0 (da wir ja den Term a 0 · y(t) transformieren
möchten), die zweite Zeile mit a 1 usw. Dies geht wegen der Linearität der Laplace-
Transformation gut; siehe Satz 4.
Danach addieren wir alles und erhalten links die linke Seite der DGL und rechts die
zugehörige Laplace-Transformierte:
(a n · s n + . . . a 1 · s 1 + a 0 ) · Y + Q n−1 (s),
wobei Q n−1 das sich ergebende Polynom vom Grad s − 1 ist.
Transformiert man nun auch noch die rechte Seite r(t)◦ •R(s), so ergibt sich die Gleichung
(a n · s n + . . . a 1 · s 1 + a 0 ) · Y + Q n−1 (s) = R(s),

5 LÖSEN LINEARER DIFFERENTIALGLEICHUNGEN 24
die wir nach Y auösen:
Y (s) =
R(s) − Q n−1 (s)
a n · s n + . . . a 1 · s 1 + a 0
.
MERKE: Nenner von Y (s)
1. Als Nenner der Transformierten von y(t) ergibt sich automatisch das charakteristische
Polynom der DGL (an der Stelle s).
Die rechte Seite ist dann noch zurückzutransformieren, um schlieÿlich die gesuchte Lösung
des AWPs, y(t), zu erhalten.
5.1.1 Beispiele
Beispiel 15
a) y ′′ − 5y ′ − 14y = 18e t , y(0) = −2, y ′ (0) = 19
b) y ′′ + 2y ′ + 5y = e −t sin (2t)
Gesucht ist diejenige Lösung, die mit Tangente y = x durch den Ursprung verläuft.
5.2 Anfangswerte für t ≠ 0
Wir wollen uns kurz davon überzeugen, dass die Annahme, dass alle Anfangswerte immer
für den Zeitpuntk t = 0 gegeben sind, keine Einschränkung bedeutet.
Nehmen wir dazu an, die Anfangswerte wären zu einem Zeitpunkt t = t 0 ≠ 0 gegeben.
METHODE: Anfangswerte für t 0 ≠ 0 gegeben
1. Lösen des AWPS als wäre t 0 = 0; dies liefert ein ỹ(t)
2. y(t) := ỹ(t − t 0 ), d.h. in ỹ(t) einfach alle t konsequent durch t − t 0 ersetzen
(Letztendlich verschieben wir also einfach den Zeitpunkt t 0 in den Ursprung des Zeitstrahls.)
5.3 Spezielle Anregungssignale
Wir betrachten wieder AWPs wie oben, d.h. mit t 0 = 0.Allerdings seien alle Anfangswerte
gleich Null, d.h. das betrachtete System sei zum Zeitpunkt t = 0 in Ruhe.
Mit Hilfe unserer Einheitsfunktionen σ(t) und δ(t) lassen sich stückweise stetige Anregungsimpulse
mit endlichem Träger modellieren. Solche rechten Seiten von DGLen
hatten wir bisher noch nicht betrachtet, können dies nun aber mit Leichtigkeit tun, da
wir die Transformierten dieser rechten Seiten berechnen können.
Beispiel 16

6 LÖSEN LINEARER DIFFERENTIALGLEICHUNGSSYSTEME 25
a) y ′′ + 5y ′ + 6y = σ(t) , y(0) = y ′ (0) = 0
b) y ′′ + 5y ′ + 6y = δ(t) , y(0) = y ′ (0) = 0
{ 4t, t < 2
c) y ′′ + 3y ′ + 2y =
0, sonst , y(0) = y′ (0) = 0
5.3.1 Zusammenhang der Lösungen für die Einheitsfunktionen
Schauen wir uns noch einmal die Ergebnisse von Beispiel 16 an, speziell der a) und b)-
Teile.
Sei y σ (t) die Lösung des a)-Teils, d.h. desjenigen AWPs, bei dem als rechte Seite die
HEAVISIDE-Funktion gewählt wurde. Analog sei y δ (t) die Lösung des Problems mit
rechter Seite gleich DIRAC-Funktion. Dann rechnet man leicht nach, dass y σ (t) ′ = y δ (t)
ist. Dies ist kein Zufall!
MERKE: y ′ σ = y δ
1. Leitet man die Lösung des AWPs mit rechter Seite = σ(t) ab, so erhält man die
Lösung des AWPs mit rechter Seite = δ(t).
Dies ist relativ leicht zu merken, wenn man bedenkt, dass auch σ(t) ′ = δ(t) gilt im Sinne
des verallgemeinerten Ableitungsbegris.
6 Lösen linearer Dierentialgleichungssysteme mittels
Laplace-Transformation
Ganz analog zur Transformation einer einzelnen Dierentialgleichung können natürlich
auch mehrere Dierentialgleichungen transformiert werden.
6.1 Vorgehensweise
Gesucht sind also m > 0 Funktionen in einer Variablen, z.B. der Zeit; x 1 (t), x 2 (t), . . . , x m (t).
Wir wollen hier annehmen, dass auch genau m lineare Dierentialgleichungen mit konstanten
Koezienten in den gesuchten Funktionen gegeben sind. Dabei dürfen allerdings
in jeder Gleichung auch alle gesuchten Funktionen auftreten!
Zusätzlich benötigen wir für eine eindeutige Lösung des Problems noch hinreichend viele
Anfangsbedingungen. Genauer benötigen wir für x k (t) Anfangsbedingungen der Art
x k (0), x ′ k (0), . . . , x(n−1)
k
(0), falls die höchste auftretende Ableitung von x k die n-te ist.
Wir transformieren nun jede Gleichung wie gehabt und werden im s-Bereich ein lineares
Gleichungssystem erhalten. Dieses wird dann im s-Bereich gelöst. Danach werden alle
Ergebnisse aus dem s-Bereich in den Zeitbereich zurücktransformiert. Dies ergibt dann
die gesuchten Funktionen x 1 (t), x 2 (t), . . . , x m (t).

6 LÖSEN LINEARER DIFFERENTIALGLEICHUNGSSYSTEME 26
METHODE: Lösen eines DGL-Systems
1. Alle Gleichungen inkl. der Anfangsbedingungen transformieren.
2. Entstehendes lineares Gleichungssysytem im s-Bereich lösen.
3. Lösungen des Gleichungssysytems in den t-Bereich zurücktransformieren.
6.1.1 Lösung des Doppelpendelsystems
Zur Illustration der Vorgehensweise kehren wir zurück zum Beispiel des Doppelpendels
aus Abschnitt 1.1.3.
Wir hatten dort ein lineares Dierentialgleichungssystem mit zwei Gleichungen erhalten:
m · l· α ..
= −ν · l· α .
−m · g · α − k · l · (α − β),
m · l· β ..
= −ν · l· β .
−m · g · β − k · l · (β − α).
(Es handelt sich dabei übrigens um ein Dierentialgleichungssystem zweiter Ordnung, da
die höchste aller überhaupt auftretenden Ableitung die zweite ist.)
Um das Beispiel zu vereinfachen, teilen wir beide Gleichungen durch (m · l):
..
α = −
m· ν α .
− g l · α − k m · α + k m · β,
..
β = − ν m· .
β − g l · β − k m · β + k m · α
und verwenden die konkreten Werte ν/m = 2, g/l = 10 und k/m = 8. Nach den Umbenennungen
x := α, y := β ergibt sich dann das folgende DGL-System, zu dem wir noch
die angegebenen (und vollkommen frei gewählten) Anfangsbedingungen hinzufügen:
..
x = −2 ẋ −18 x + 8 y,
..
y = −2 ẏ −18 y + 8 x,
AW: x(0) = 0,
.
x (0) = 1, y(0) = 0,
.
y (0) = 0.
(Die Anfangsbedingungen bedeuten, dass sich beide Pendel am Tiefpunkt benden. Eines
von beiden besitzt aber eine von Null verschiedene Anfangsgeschwindigkeit.)
1. Schritt: Transformation
x(t) ◦ • X(s)
.
x (t) ◦ • s · X(s) − x(0)
..
x (t) ◦ • s 2 · X(s) − s · x(0)− ẋ (0)
y(t) ◦ • Y (s)
.
y (t) ◦ • s · Y (s) − y(0)
..
y (t) ◦ • s 2 · Y (s) − s · y(0)− ẏ (0)

6 LÖSEN LINEARER DIFFERENTIALGLEICHUNGSSYSTEME 27
Nach Einsetzen den Anfangswerte erhalten wir also das lineare Gleichungssystem
s 2 X − 1 = −2sX − 18X + 8Y,
s 2 Y = −2sY − 18Y + 8X bzw.
X(s 2 + 2s + 18) − 8Y = 1
Y (s 2 + 2s + 18) − 8X = 0.
2. Schritt: Lösen des Gleichungssystems Man beachte, dass X und Y gesucht sind
und s wie ein Parameter zu behandeln ist. Um die Übersicht zu behalten, empehlt es
sich, das lineare Gleichungssystem in Matrixschreibweise zu schreiben:
( s 2 + 2s + 18 −8
−8 s 2 + 2s + 18
) ( X
·
Y
) ( 1
=
0
Das hat auch den Vorteil, dass wir jetzt die Unbekannten mittels der CRAMERschen
Regel bestimmen können:
∣ 1 −8
0 s 2 + 2s + 18 ∣
s
X =
2 + 2s + 18
∣ s2 + 2s + 18 −8
=
(s 2 + 2s + 18) 2 − 64 ,
−8 s 2 + 2s + 18 ∣
∣ s2 + 2s + 18 1
−8 0 ∣
8
Y =
∣ s2 + 2s + 18 −8
=
(s 2 + 2s + 18) 2 − 64 .
−8 s 2 + 2s + 18 ∣
. . .
3. Schritt: Rücktransformation der Lösungen
. . .
6.1.2 Weiteres Übungsbeispiel
Beispiel 17
mit den Anfangsbedingungen
Lösen Sie das lineare Dierentialgleichungssystem
mittels LAPLACE-Transformation.
.
x (t) − x(t) + y(t) = − cos t,
.
y (t) − 4x(t) − y(t) = sin t + cos t
x(0) = 1, y(0) = −1.
)
.

7 DIE EIN-AUSGABE-RELATION EINES LINEAREN SYSTEMS 28
7 Die Ein-Ausgabe-Relation eines linearen Systems
7.1 Problemstellung
Die wohl interessantestes Anwendung der LAPLACE-Transformation ist die Untersuchung
der Ein-Ausgabe-Relation eines linearen Systems.
Als lineares System bezeichnen wir dabei eine wie in Abbildung 13 dargestellte black box,
die folgende Eigenschaften hat:
• Verstärkung: Ersetzt man den Input-Signal x(t) durch λ · x(t) (mit λ ∈ R), so
ergibt sich als Output-Signal λ · y(t).
• Überlagerung: Werden x 1 (t) und x 2 (t) in y 1 (t) bzw. y 2 (t) übersetzt, so wird
x 1 (t) + x 2 (t) in y 1 (t) + y 2 (t) übersetzt.
Abbildung 13: Lineares System mit Ein- und Ausgangssignal
Die Frage ist nun, wie x(t) und y(t) miteinander zusammenhängen. Wie sich herausstellen
wird, hat man diesen Zusammenhang interessanterweise vollständig verstanden, sobald
man die Antwort des Systems auf den DIRAC-Impuls kennt. Wir führen also folgende
Begrie ein:
Denition 5 (Impuls- und Sprungantwort)
Für x(t) = δ(t) nennt man die zugehörige Antwort eines gegebenen linearen System
die Impulsantwort; y δ (t).
Analog bezeichnet y σ (t) die Sprungantwort, d.h. die Antwort auf den Input x(t) = σ(t).
Um dies zu erarbeiten machen wir einige...
7.2 Allgemeine Betrachtungen
Da unser Eingangssignal x(t) die Rolle der Störfunktion, d.h. der rechten Seite spielt,
ergibt sich eine Dierentialgleichung der Form
a n · y (n) (t) + . . . a 2 · y ′′ (t) + a 1 · y ′ (t) + a 0 · y(t) = x(t),
wobei wir also annehmen wollen, dass die Koezienten a k konstant sind und nicht von t
abhängen.

7 DIE EIN-AUSGABE-RELATION EINES LINEAREN SYSTEMS 29
Als Transformationspaare erhalten wir:
x(t) ◦ • X(s) sowie
y(t) ◦ • Y (s)
y ′ (t) ◦ • s · Y (s) − y(0)
y ′′ (t) ◦ • s 2 · Y (s) − s · y(0) − y ′ (0)
.
Unter der Annahme, dass das System zum Zeitpunkt t = 0 in Ruhe ist, sind alle Anfangsbedingungen
gleich Null, fallen also weg.
Wir multiplizieren die Transformationen mit den passenden Koezienten a k und bekommen
im s-Bereich die Gleichung
Y (s) · [a
n s n + · · · + a 2 s 2 + a 1 s + a 0
]
= X(s) bzw.
Y (s)
X(s)
=
1
a n s n + · · · + a 2 s 2 + a 1 s + a 0
.
Interessanterweise hängt der Quotient Y (s)/X(s) also gar nicht vom Eingangs- oder Ausgangssignal
ab. Diese kürzen sich im s-Bereich quasi weg. Übrig bleibt ein Term (auf der
rechten Seite), der nur von den Koezienten aus der Dierentialgleichung abhängt. Genauer
steht im Nenner das charakteristische Polynom, p char (s), der Dierentialgleichung.
Dies gibt Anlass zu folgender Denition:
Denition 6 (Übertragungsfunktion)
Gegeben sei ein lineares System, dessen Verhalten sich durch eine lineare Dierentialgleichung
mit konstanten Koezienten beschreiben lässt.
Sei x(t) ein Eingangs- und y(t) das zugehörige Ausgangssignal mit den LAPLACE-
Tranformierten X(s) bzw. Y (s). Dann heiÿt
G(s) :=
1
p char (s)
Übertragungsfunktion im s-Bereich oder auch Frequenzgang des Systems.
Die Rücktransformierte g(t) ◦ • G(s) heiÿt Übertragungsfunktion im t-Bereich oder
auch Transferfunktion des Systems.
Wie G(s) ist natürlich auch g(t) unabhängig vom Eingangs- oder Ausgangssignal.
Nach dem Faltungssatz, Satz 13, gilt
y(t) ◦ • Y (s) = X(s) · G(s) • ◦ x ∗ g (t) .

7 DIE EIN-AUSGABE-RELATION EINES LINEAREN SYSTEMS 30
Satz 14 (Berechnung des Ausgangssignals)
Ist g(t) die Tranferfunktion eines linearen Systems, so berechnet sich das zum Eingangssignal
x(t) gehörende Ausgangssignal y(t) gemäÿ der Formel
y(t) = x ∗ g (t) .
Wir hatten einerseits gesehen, dass wir die Tranferfunktion g(t) als Rücktransformierte
von G(s) = 1/p char (s) berechnen können. Andererseits gilt aber wegen δ(t) ◦ • 1 auch
y δ ◦ • Y δ (s) = 1 · G(s) = G(s) • ◦ g(t), bzw. kurz:
Satz 15 (Tranferfunktion = Impulsantwort)
Für ein lineares System gilt g(t) = y δ (t).
Die Tranferfunktion stimmt also mit der Impulsantwort überein. Man könnte also sagen,
dass man alles über das System herausbekommt, indem man sich die Antwort auf den
Einheitsimpuls besorgt.
Man kommt aber auch von der Sprungantwort auf die Transferfunktion, da ja y ′ σ(t) = y δ (t)
gilt. D.h. man kann auch einfach die Sprungantwort berechnen und diese dann dierenzieren.
Wir schauen uns der Vollständigkeit halber noch die Transformierte der Sprungantwort
an. Wegen σ(t) ◦ • 1/s ist das einfach; und zwar
y σ (t) ◦ • Y σ (s) = 1 s
· G(s) =
G(s)
s
=
1
s · p char (s) .
Abbildung 14 fasst noch einmal die wichtigsten Erkenntnisse aus den zurückliegenden
Sätzen und Betrachtungen zusammen.
7.3 Beispiele
7.3.1 Das R − c − Glied
Wir kehren noch einmal zum R − c − Glied aus Abbildung 4 zurück. Dabei betrachten
wir nun u in als Eingangssignal x(t) und u out als gesuchtes Ausgangssignal y(t).
Das OHMsche Gesetz liefert:
R = u R
i(t) = u in − u out
i(t)
=
x(t) − y(t)
,
i(t)
d.h. x(t) − y(t) = R · i(t). Der Strom i(t) ist proportional zur zeitlichen Änderung der
Spannung über dem Kondensator, d.h.
i(t) = c · d
dt u c(t) = c· ẏ (t),

7 DIE EIN-AUSGABE-RELATION EINES LINEAREN SYSTEMS 31
Abbildung 14: Transfer- und Übertragungsfunktion und weitere wichtige Formeln
wobei der Proportionalitätsfaktor c der Kapazität entspricht.
Insgesamt folgt also die lineare Dierentialgleichung erster Ordnung
Rc· ẏ (t) + y(t) = x(t),
mit konstanten Koezienten. Wir können also unsere entwickelte Maschinerie auf das
Problem anwenden.
Beispiel 18 Man berechne für das R − c − Glied die Impulsantwort, die Sprungantwort
sowie mittels Faltung die Antwort auf das Rechtecksignal x r (t) := u 0 · (σ(t − t 1 ) −
σ(t − t 2 )), wobei u 0 > 0 und 0 ≤ t 1 < t 2 seien.
. . .