Wahrscheinlichkeit & Statistik Musterlösung Serie ... - FIM - ETH Zürich

ETH Zürich FS 2013
D-MATH
Hans Rudolf Künsch
Koordinator
Blanka Horvath
Wahrscheinlichkeit & Statistik
Musterlösung Serie 14
1. Beim Neyman-Pearson-Test der Hypothese H 0 : X ∼ f(x) dx gegen die Alternative
H A : X ∼ f(x − 1) dx wird der Verwerfungsbereich bestimmt durch die
Ungleichung
f(x − 1)
f(x)
> c = c(α).
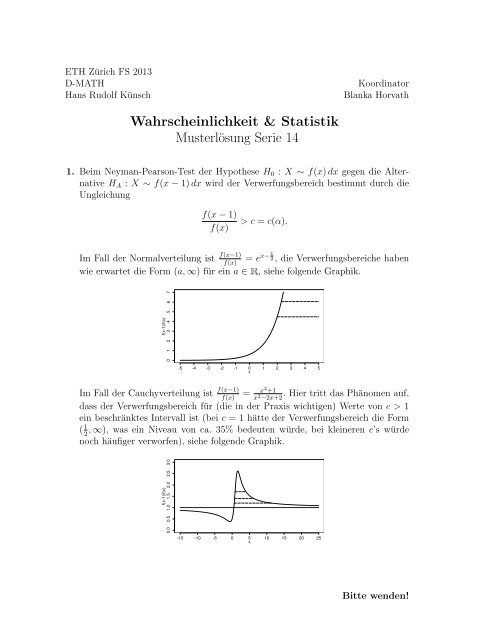
Im Fall der Normalverteilung ist f(x−1) = e x− 1 2 , die Verwerfungsbereiche haben
f(x)
wie erwartet die Form (a, ∞) für ein a ∈ R, siehe folgende Graphik.
f(x-1)/f(x)
0 1 2 3 4 5 6 7
-5 -4 -3 -2 -1 0 1 2 3 4 5
x
Im Fall der Cauchyverteilung ist f(x−1) = x2 +1
. Hier tritt das Phänomen auf,
f(x) x 2 −2x+2
dass der Verwerfungsbereich für (die in der Praxis wichtigen) Werte von c > 1
ein beschränktes Intervall ist (bei c = 1 hätte der Verwerfungsbereich die Form
( 1 , ∞), was ein Niveau von ca. 35% bedeuten würde, bei kleineren c’s würde
2
noch häufiger verworfen), siehe folgende Graphik.
f(x-1)/f(x)
0.0 0.5 1.0 1.5 2.0 2.5 3.0
-15 -10 -5 0 5 10 15 20 25
x
Bitte wenden!

Die Erklärung ist, dass bei der Cauchyverteilung sehr grosse Werte sowohl unter
H 0 als auch unter H A etwa gleich unwahrscheinlich sind. Deshalb ist es für nicht
allzu grosse Werte von α beser, bei grosser Beobachtung X die Nullhypothese
nicht zu verwerfen.
Bei der Normalverteilung tritt dieses Phänomen nicht auf, da grosse X unter der
Alternativhypothese sehr viel weniger unwahrscheinlich sind als unter H 0 .
2. Betrachte folgende Figur:
f 1(x)
f (x)
0
f (x)
0
α
f (x) 1
Verwerfungsbereich
0 1/2 1 3/2
a) Für α ∈ (0, 1 2 ] wähle K′ ⊆ ( 1 2 , 1) mit µ L(K ′ ) = α (ist die Situation in
der Figur) und als Verwerfungsbereich K = K ′ ∪ [1, ∞). Dieser Test ist
offensichtlich ein mächtigster Test zum Niveau α, und es gilt φ = 1, falls
f 1 (x) > f 0 (x), und φ = 0, falls f 1 (x) < f 0 (x) (also c = 1).
Für α ∈ [ 1, 1) wähle 2 K′ ⊆ (0, 1) mit µ 2 L(K ′ ) = α − 1 und den Verwerfungsbereich
K = K ′ ∪ ( 1 , ∞). Auch dieser Test ist mächtigst zum Niveau α, und
2
2
er erfüllt die Bedingungen vom Skript mit c = 0.
Solche Tests sind nicht eindeutig, da K ′ eine beliebige Teilmenge von ( 1, 1) 2
bzw. von (0, 1 ) sein kann.
2
b) Für α ∈ ( 1, 1) (zum Beispiel für α = 3) wähle K = ( 1 , ∞). Dieser Test
2 4 2
verwirft immer, wenn die Alternative wahr ist. Er hat also maximale Macht
E 1 [φ] = 1, obwohl er das zur Verfügung stehende Niveau nicht einmal ganz
ausnützt: E 0 [φ] = 1 < 3.
2 4
Siehe nächstes Blatt!

3. Beim Vorzeichentest der Nullhypothese F −1 (0.5) = m lautet die Teststatistik
T n,m = ∑ n
i=1 I [X i >m] und der Test ist gegeben durch
ϕ(x) = 1 falls ∣ Tn,m − n ∣
2 > c(n, α),
wobei x = (x 1 , . . . , x n ) die Beobachtungen, n die Anzahl der Beobachtungen und
α das Niveau des Tests bezeichnet. Weil F als stetig angenommen wurde, ist T n,m
unter der Nullhypothese Bin(n, 0.5)-verteilt. Also ist k = n − c(n, α) bestimmt
2
durch
∑k−1
( n
k∑
( n
0.5
j)
n ≤ α < 0.5
2
j)
n ,
j=0
und n 2 + c(n, α) = n − k. Wenn wir C ⊂ Rn+1 definieren durch
j=0
C = {(x 1 , . . . , x n , m); k ≤
n∑
I [xi >m] ≤ n − k},
i=1
dann ist der Schnitt A(m) = {(x 1 , . . . , x n ); (x 1 , . . . , x n , m) ∈ C} der Annahmebereich
des Vorzeichentests zum Niveau α. Mit dem Dualitätssatz bildet der
Schnitt B(x) = {m; (x 1 , . . . , x n , m) ∈ C} daher einen Vertrauensbereich zum
Niveau 1 − α. Wenn x (1) < x (2) < . . . < x (n) die der Grösse nach geordneten
Beobachtungen bezeichnet, dann gilt
m ∈ [x (j) , x (j+1) ) ⇔
n∑
I [xi >m] = n − j.
i=1
Also ist m ∈ B(x) genau dann, wenn x (k) ≤ m < x (n+1−k) , d.h. (X (k) , X (n+1−k) )
ist ein Vertrauensintervall für den Median zum Niveau 1 − α (weil F als stetig
angenommen wurde, spielt es keine Rolle, ob man das offene oder abgeschlossene
Intervall nimmt). Wegen des zentralen Grenzwertsatzes ist c(n, 0.95) ≈
1.96 √ n/4 ≈ √ n, also ist das Intervall genähert gleich (X (n/2−
√ n) , X (n/2+
√ n) ).
4. a) 1. Sei X die Zufallsvariable welche die Länge der Karotten modelliert, getestes
wird auf den Parameter µ = E[X], die durchschnittliche Länge
der Karotten. Die Nullhypothese ist die Behauptung des Gemüsehändlers,
wir wollen testen ob sie sich widerlegen lässt, daraus ergibt sich ein
linksseitiger Test mit µ 0 = 30cm und den Hypothesen H 0 : µ ≥ µ 0 H A :
µ < µ 0 .
2. Zweiseitiger Test mit µ 0 = 50g sowie den Hypothesen H 0 : µ = µ 0 H A :
µ ≠ µ 0 .
3. Rechtsseitiger Test mit µ 0 = 3mm sowie den Hypothesen H 0 : µ ≤
µ 0 H A : µ > µ 0 .
Bitte wenden!

4. Hier modelliert die Zufallsvariable X mit Wertebereich W X = [0, 1]
den Anteil an holzigen Spargel, getestet wird wieder auf den durchschnittlichen
Wert davon, also auf µ = E[X], aus der Behauptung des
Gemüsehändlers ergibt sich ein rechtsseitiger Test mit µ 0 = 0.003 sowie
den Hypothesen H 0 : µ ≤ µ 0 H A : µ > µ 0 .
5. Zweiseitiger Test mit µ 0 = 0.4 sowie den Hypothesen H 0 : µ = µ 0 H A :
µ ≠ µ 0 .
b) Die Nullhypothese wurde verworfen obwohl sie stimmt, d.h. Fehler 1.Art.
c) Die Nullhypothese wurde nicht verworfen obwohl sie falsch ist, d.h. Fehler
2.Art.
Bemerkung: Da wir ehrliche Gemüsehändler nicht ungerechtfertigt in Misskredit
bringen wollen, müssen wir die Wahrscheinlichkeit für einen Fehler 1.Art gering
halten, d.h. wenn wir seine Behauptung anzweifeln, dann müssen wir einen guten
Grund haben dafür, und dieser ist die geringe Wahrscheinlichkeit für eine
bestimmte Gesamtheit von Testausgängen falls die Behauptung stimmt (Fehler
1.Art). Da es im Allgemeinen nicht gelingt beide Fehler klein zu halten, bedeutet
ein Akzeptieren der Nullhypothese nicht, dass die Behauptung stimmt, sie konnte
lediglich nicht widerlegt werden. Der Gemüsehändler ist also auf der sicheren Seite,
sagt er die Wahrheit, dann hat er kaum was zu befürchten (Fehler 1.Art), und
wenn er lügt, dann hat er in bestimmten Fällen sogar ein gute Chance (Fehler
2.Art) nicht entlarvt zu werden.
5. a) Die Stichprobe ist ungepaart.
b) Da getestet werden soll, ob das Getränk eine positive Wirkung hat, wird
einseitig getestet.
c) Die Alternativhypothese, die von den vier Möglichkeiten am besten passt ist
in dem Fall die Nummer 3., d.h. Das Getränk bewirkt eine bessere Leistung.
Bemerkung: Die Nullhypothese lautet, dass die Leistung nach Einnahme des
Getränkes genausogut oder schlechter ist.
d) 1. richtig: Der P -Wert ist das kleinste Niveau, auf dem die Nullhypothese
verworfen wird, und 0.01 < 0.034.
2. falsch: Das Niveau gibt die Wahrscheinlichkeit an, die Nullhypothese
zu verwerfen, obwohl sie richtig ist. Bei kleinerem Niveau wird daher
weniger oft verworfen.
3. richtig: Fehler 1. Art heisst, die Nullhypothese zu verwerfen, obwohl sie
richtig ist.
Siehe nächstes Blatt!

4. falsch: Beim t-Test ist das Niveau nur exakt richtig unter Normalverteilung,
beim Wilcoxon-Test hingegen für beliebige stetige Verteilungen.
5. richtig: Folgt aus dem Dualitätssatz. Der Annahmebereich bei α =1%
ist grösser als bei α =5% (vergleiche 2.)
6. richtig: Je kleiner |µ|, desto näher liegt die Alternative bei der Nullhypothese,
und desto eher entscheidet man sich für die Nullhypothese statt
für die Alternative.