Lineare Algebra

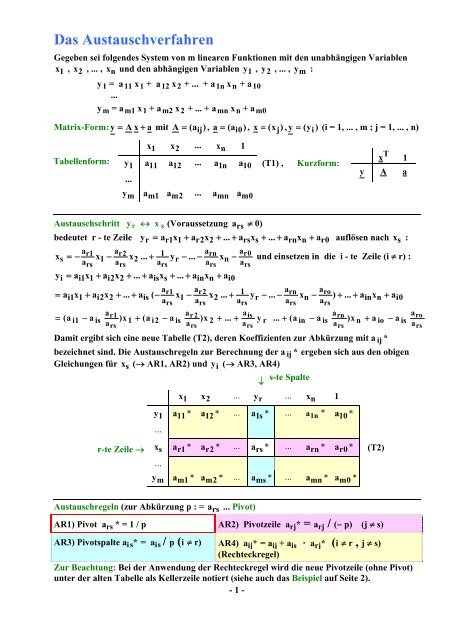
Das AustauschverfahrenGegeben sei folgendes System von m linearen Funktionen mit den unabhängigen Variablenx 1 , x 2 , ... , x n und den abhängigen Variablen y 1 , y 2 , ... , y m :y 1 = a 11 x 1 + a 12 x 2 + ... + a 1n x n + a 10...y m = a m1 x 1 + a m2 x 2 + ... + a mn x n + a m0Matrix-Form: y A x a mit A (aij), a (ai0), x (xj), y (yi) (i = 1, ... , m ; j = 1, ... , n)Tabellenform:x 1 x 2 ... x n 1y 1 a 11 a 12 ... a1na 10...yma m1a m2... amna m 0(T1) ,Kurzform:Tx 1y A aAustauschschritt y r x s (Voraussetzung a rs 0)bedeutet r - te Zeile yr ar1x1 ar2x2 ... arsxs ... arnxn ar0auflösen nach x s :ar1ar2arnax1r0s x1 xa a 2 ... ya r ... xa n und einsetzen in die i - te Zeile (i r) :ars rs rsrs rsyi ai1x1 ai2x2 ... aisxs ... ainxn ai0a aa a a1i1x1 ai2x2 ... ais( r1xa 1 r2xa 2 ... ya r ... rnxroa n ) ... aa inxn ai0rs rs rsrs rsar1ar 2aisa ( arni1 a is )x 1 (a i2 aais )x 2 ... y r ... (a in a is )x n a io a isrsarsarsarsDamit ergibt sich eine neue Tabelle (T2), deren Koeffizienten zur Abkürzung mit a ij *bezeichnet sind. Die Austauschregeln zur Berechnung der a ij * ergeben sich aus den obigenGleichungen für x s ( AR1, AR2) und y i ( AR3, AR4)s-te Spaltex 1 x 2 ... y r ... x n 1y 1 a 11 * a 12 * ... a 1s* ... a 1n* a 10 *...aroarsr-te Zeile x s a r1* a r2* ... a rs * ... a rn * a r0*...y m a m1* a m2* ... a ms * ... a mn * a m0*(T2)Austauschregeln (zur Abkürzung p : = a rs ... Pivot)AR1) Pivot a rs * = 1 / p AR2) Pivotzeile a rj * = a rj / ( p) (j s)AR3) Pivotspalte a i s * = a i s / p (i r) AR4) a ij * = a ij + a is a rj * (i r , j s)(Rechteckregel)Zur Beachtung: Bei der Anwendung der Rechteckregel wird die neue Pivotzeile (ohne Pivot)unter der alten Tabelle als Kellerzeile notiert (siehe auch das Beispiel auf Seite 2).- 1 -

Lösung linearer GleichungssystemeGegeben sei das lineare Gleichungssystema 11 x 1 + a 12 x 2 + ... + a 1n x n = b 1... (1)a m1 x 1 + a m2 x 2 + ... + a mn x n = b mMatrix-Form: A x b (1') mit A (aij), x (xj), b (bi) (i = 1, ... , m ; j = 1, ... , n)Tabellenform:xTÄquivalente Form: y A x b mit y o ,1(1'')y=o A bLösungsprinzip: Austauschverfahren mit Spaltentilgung (AVS)Fall 1: Alle y i austauschbar (1) ist lösbar, Lösung aus letzter Tabelle (TE) ablesbar,die nicht ausgetauschten x j (Nichtbasisvariable NBV) sind frei wählbar,die ausgetauschten x j (Basisvariable BV) lassen sich durch die NBV ausdrückenFall 2: Wenigstens ein y i ist gegen kein x j austauschbar, in der 1-Spalte der entsprechendenZeile stehe die Zahl , dannFall 2a: = 0 Zeile (0 = 0) kann gestrichen werdenFall 2b: 0 Gleichungssystem (1) ist nicht lösbarBeispiel:5 x 1 3 x 2 + x 3 = 18x 1 +4 x 2 +2x 3 = 3.... Pivot , Beispielrechnung für Rechteckregel:5 2 + 1 = 9T1 x 1 x 2 x 3 1 PT2 x 1 x 2 1 PT3 x 1 1 P0 5 3 1 18 15x 3 5 3 18 15x 3 2,3 6,330 1 4 2 3 10K 5 3 * 18 150 9 10 39 40K 0,9 * 3,9 4x 2 0,9 3,9 4T3 ist Endtabelle, Lösung: x 1 = t , x 2 = 0,9 t 3,9 , x 3 = 2,3 t + 6,3 (t R)Probe (optional), s. Seite 3Bemerkungen:1. Anstelle AVS kann auch AVSZ durchgeführt werden, dabei Kellerzeilen nicht mit Kmarkieren, sondern mit den ausgetauschten x j , am Ende Rückrechnung mit denKellerzeilen in umgekehrter Reihenfolge durchführen (= GAUSS-Algorithmus)2. Bei einem homogenen System (b = o) kann die 1-Spalte (lauter Nullen!) entfallen. Sie muss am Ende natürlich berücksichtigt werden!- 2 -yTxA

Probe beim Austauschverfahren (optional)Zusatzspalte in T1 so eintragen, dass alle Zeilensummen gleich 1 sind, außer inden Zeilen, die den sogenannten Hilfsvariablen y i = 0 beim Austauschverfahrenmit Spaltentilgung entsprechen. Diese Zeilensummen müssen gleich 0 sein. Nachdem Austausch müssen die Zeilensummen = 1 sein, mit Ausnahme der obengenannten y-Zeilen beim AVS und AVSZ (dort Zeilensummen = 0). Beim AVSZist auch die Kellerzeile zu überprüfen (Zeilensumme = 1).Weitere Anwendungen des AustauschverfahrensxT(jeweils mit der Starttabelle )y A Inverse einer (n,n)-Matrix, vollständiges AV, Fall 1: Alle y i austauschbar A ist regulär, nach Ordnen von Zeilen und Spalten ist A 1aus TE ablesbar,Fall 2: Nicht alle y i austauschbar A ist singulär Rang einer Matrix, AVSZ , rang(A) = Anzahl der ausführbarenAustauschschritte Lineare Unabhängigkeit von Vektoren a 1, ... , a n überprüfen,Ansatz x 1 a 1+ ... + x na n = o A x = o , dabei A .... Matrix mit denSpaltenvektoren a 1, ... , a n , AVS, die zu den ausgetauschten x j (BV)gehörenden a j sind unabhängig, sie bilden eine Basis von L(a 1, ... , a n) Determinante einer (n,n)-Matrix: AVSZ ,det A = 0 , falls rang (A) < n, anderenfalls gilti j i ji jdet A ( 1) 1 1 p1( 1) 2 2 p2... ( 1) n n pn,dabei p k ... Pivot im k-ten Austauschschritt, i k bzw. j k ... Zeilen- bzw.Spaltennummer des Pivots in der jeweiligen Tabelle Tk.- 3 -