- Page 1 and 2: T H E S E C O N D SCIENTIFCC - L ME
- Page 3 and 4: The 2nd SCIENTIFIC AMERICAN Book of
- Page 5 and 6: Material previously published in Sc
- Page 7 and 8: INTRODUCTION CONTENTS The Five Plat
- Page 9 and 10: INTRODUCTION SINCE THE APPEARANCE o
- Page 11 and 12: Introduction 11 socialism and capit
- Page 13 and 14: TETRAHEDRON / The Five Platonic Sol
- Page 15 and 16: 16 The Five Platonic Solids both la
- Page 17 and 18: 18 The Five Platonic Solids value o
- Page 19 and 20: 20 The Five Platonic Solids tance i
- Page 21 and 22: 22 Tlre Five Platonic Solids ANSWER
- Page 23 and 24: CHAPTER TWO w Tetrajlexagons H EXAF
- Page 25 and 26: 26 Tetrnflezagons are joined by two
- Page 27 and 28: A different variety of tetraflexago
- Page 29 and 30: FIG. 11. How to make and flex the f
- Page 31 and 32: C H A P T E R THREE Henry Ernest Du
- Page 33 and 34: 34 Henry Ernest Dudeney: England's
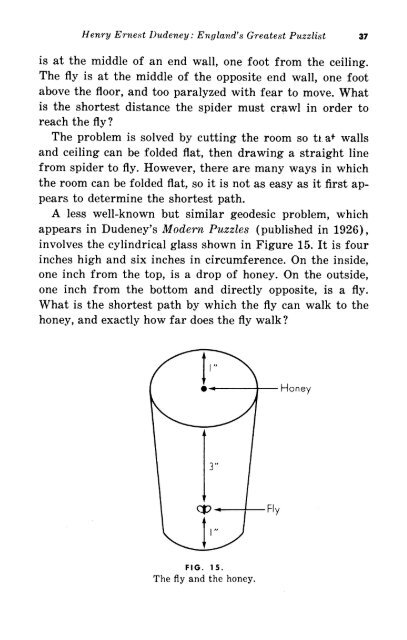
- Page 35: 36 Henry Ernest Llzcdeney: Englnvd'
- Page 39 and 40: 40 Henry Ernest Dudeney: England's
- Page 41 and 42: 42 Henry Ernest Dudeney: England's
- Page 43 and 44: I)i,qitnl Roots FIG. 19. Symbols fo
- Page 45 and 46: 46 Digital Roots Since the answer i
- Page 47 and 48: 48 Digital Roots what cards are at
- Page 49 and 50: Digital Roots ANSWERS IN THE GAME p
- Page 51 and 52: FIG. 21. The twiddled bolts. planes
- Page 53 and 54: 54 Nine Problenzs two units that is
- Page 55 and 56: 56 Nine Problems depicted at bottom
- Page 57 and 58: Nine Problems FIG. 24. The flight a
- Page 59 and 60: 60 Nine Problems men who shook hand
- Page 61 and 62: 62 Nine Problems As we saw earlier,
- Page 63 and 64: 64 Nine Pro Blems against his own b
- Page 65 and 66: 66 The Soma Cube Tix, are discussed
- Page 67 and 68: 68 The Soma Cube set of the pieces
- Page 69 and 70: WALL SKYSCRAPER DOG PYRAMID FIG. 29
- Page 71 and 72: the top illustration of Figure 30.
- Page 73 and 74: 74 The Soma Cube
- Page 75 and 76: 76 The Soma Cuhe Some of these figu
- Page 77 and 78: CHAPTER SEVEN Recreational Topology
- Page 79 and 80: Recreational Topology FIG. 33. Stew
- Page 81 and 82: Ree~eational Topology FIG. 34. The
- Page 83 and 84: 84 Recreational Topology has taken
- Page 85 and 86: 86 Rec~eational Topology game is pl
- Page 87 and 88:
88 Recreational Topology ANSWERS TH
- Page 89 and 90:
90 Phi: The Golden Ratio is commonl
- Page 91 and 92:
Phi: The Golden Ratio FIG. 39. The
- Page 93 and 94:
94 Phi: The Golden Ratio volved in
- Page 95:
96 Phi: The Golden Ratio There is a
- Page 98 and 99:
Phi: The Golden Ratio THE SACRAMENT
- Page 100 and 101:
Phi: The Golden Ratio 101 culate ph
- Page 102 and 103:
Phi: The Golden Ratio 103 The two e
- Page 104 and 105:
The Monkeg and the Coconuts 105 foo
- Page 106 and 107:
The Monkey and the Coconuts 107 Dir
- Page 108 and 109:
The Monkey and the Coconuts 109 the
- Page 110 and 111:
The Monkey and the Coconuts 11 1 le
- Page 112 and 113:
Woodstock in the 12th century by Ki
- Page 114 and 115:
FIG. 49. A "simply connected" maze
- Page 116 and 117:
Mazes 117 tiply connected maze whic
- Page 118 and 119:
A CHAPTER E L E V E N rn Recreation
- Page 120 and 121:
Recreational Logic 121 man, so we p
- Page 122 and 123:
Recreational Logic 123 1. In 1918,
- Page 124 and 125:
Recreational Logic 125 truth. Since
- Page 126 and 127:
Recreational Logic 127 stand" or "W
- Page 128 and 129:
Recrecrtionnl Logic 129 solution is
- Page 130 and 131:
Magic Squares 131 order three. An e
- Page 132 and 133:
Magic Squares 133 FIG. 54. Albrecht
- Page 134 and 135:
Magic Squares 135 can be restored b
- Page 136 and 137:
Magic Sqzlnres 137 seen by transfer
- Page 138 and 139:
Magic Squares 139 in Rochester, New
- Page 140 and 141:
C H A P T E R T H I R T E E N James
- Page 142 and 143:
James Hugh Riley Shows, Inc. 143 fe
- Page 144 and 145:
James Hugh Riley Shows, Inc. 145 ha
- Page 146 and 147:
James Hugh Riley Shou.s, Inc. 147 "
- Page 148 and 149:
James Hugh Riley Shows, Inc. 149 ha
- Page 150 and 151:
James Hug11 Riley Shows, Inc. 151 e
- Page 152 and 153:
Nine More Prohlems 153 Mr. Jones ha
- Page 154 and 155:
Nine More Problems 155 ing it the t
- Page 156 and 157:
Nine Afore Problems 157 a journey o
- Page 158 and 159:
Nine More Prohlerns 159 (This was t
- Page 160 and 161:
Nine More Problems 161 (which gives
- Page 162 and 163:
Nine More Problems 163 We know that
- Page 164 and 165:
C H A P T E R F I F T E E N Eleusis
- Page 166 and 167:
Eleusis : The Induction Game 167 pl
- Page 168 and 169:
Eleusis : The Induction Game 169 To
- Page 170 and 171:
Eleusis: The Indz~ction Game 171 Th
- Page 172 and 173:
Eleusis : The Induction Game 173 co
- Page 174 and 175:
Origami 175 past 20 years there has
- Page 176 and 177:
Paper can also be folded to produce
- Page 178 and 179:
Origami 179 At what spot along the
- Page 180 and 181:
Origami 181
- Page 182 and 183:
ADDENDUM SINCE this chapter appeare
- Page 184 and 185:
Origami 185 crease. If the value to
- Page 186 and 187:
Squaring the Square 187 H. Stone, n
- Page 188 and 189:
FIG. 73. Sqzcnring the Sqziare FIG.
- Page 190 and 191:
Squaring the Square 191 gram. But S
- Page 192 and 193:
Squaring the Square 193 out any ref
- Page 194 and 195:
Squaring the Square 195 and eventua
- Page 196 and 197:
Squaring the Sqz~are 112 FIG. 78. 3
- Page 198 and 199:
Squaring the Square 199 But I thoug
- Page 200 and 201:
Squaring the Square 201 each diagra
- Page 202 and 203:
Squaring the Square 203 FIG. 82. si
- Page 204 and 205:
Squaring the Square 205 team solved
- Page 206 and 207:
Squaring the Square 207 first is to
- Page 208 and 209:
Squaring the Square 209 fifth-dimen
- Page 210 and 211:
Mechanical Puzzles 21 1 about 2,000
- Page 212 and 213:
Mecl~nnicnl Puzzles 213 Dissection
- Page 214 and 215:
Mechanical Puzzles 215 is shown in
- Page 216 and 217:
Mechanical Puzzles 217 ulated a cer
- Page 218 and 219:
Mechanical Puzzles 219 symmetrical
- Page 220 and 221:
Probability and Ambiguity 22 1 ple
- Page 222 and 223:
Probability and Amhig~iity 223 now
- Page 224 and 225:
Probability and Ambiguity 225 study
- Page 226 and 227:
Probability and Ambiguity 227 that
- Page 228 and 229:
Probability and Ambiguity 229 David
- Page 230 and 231:
oric, or 213, a~itl A's arc 113. In
- Page 232 and 233:
CHAPTER TWENTY w The Mysterious Dr.
- Page 234 and 235:
The Mysterious Dr. Matrix FIG. 91.
- Page 236 and 237:
The Mysterious Dr. Matrix 237 the m
- Page 238 and 239:
The Mysterious DT; Matrix 239 denti
- Page 240 and 241:
The Mysterious Dr. Matrix 241 read
- Page 242 and 243:
The Mysterious Dr. Matrix 243 Note
- Page 244 and 245:
246 References for Further Reading
- Page 246 and 247:
248 References for Further Reading
- Page 248 and 249:
250 References for Further Reading
- Page 251 and 252:
POSTSCRIPT, 1987 No EFFORT has been
- Page 253 and 254:
ABOUT THE AUTHOR MARTIN GARDNER has