Chapter 4 Linear Differential Operators

140 CHAPTER 4. LINEAR DIFFERENTIAL OPERATORS
A solution with eigenvalue E = k2 and satisfying the boundary condition at
r = 0 is
A sin(kr), r < a,
ψ(r) =
(4.132)
sin(kr + η), r > a.
The conditions to be satisfied at r = a are:
i) continuity, ψ(a − ɛ) = ψ(a + ɛ) ≡ ψ(a), and
ii) jump in slope, −ψ ′ (a + ɛ) + ψ ′ (a − ɛ) + λψ(a) = 0.
Therefore,
ψ ′ (a + ɛ)
ψ(a) − ψ′ (a − ɛ)
= λ, (4.133)
ψ(a)
or
Thus,
and
−π
k cos(ka + η)
sin(ka + η)
− k cos(ka)
sin(ka)
= λ. (4.134)
cot(ka + η) − cot(ka) = λ
, (4.135)
k
η(k) = −ka + cot −1
η(k)
π 2π 3π 4π
λ
+ cot ka . (4.136)
k
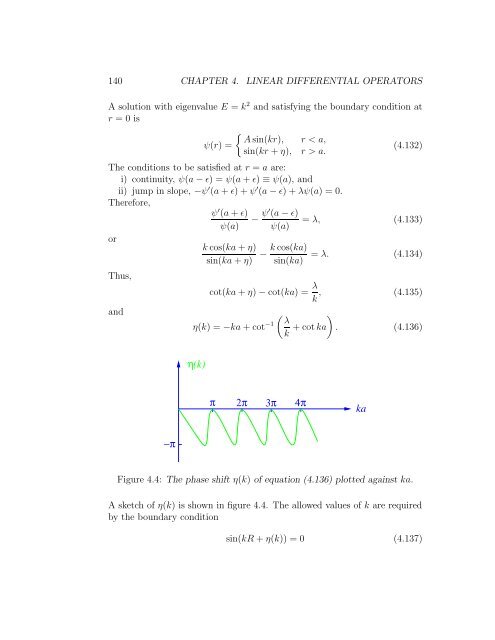
Figure 4.4: The phase shift η(k) of equation (4.136) plotted against ka.
A sketch of η(k) is shown in figure 4.4. The allowed values of k are required
by the boundary condition
ka
sin(kR + η(k)) = 0 (4.137)