Exploring the microscopic origin of magnetic anisotropies with X-ray ...

J. Sto( hr / Journal of Magnetism and Magnetic Materials 200 (1999) 470}497 485
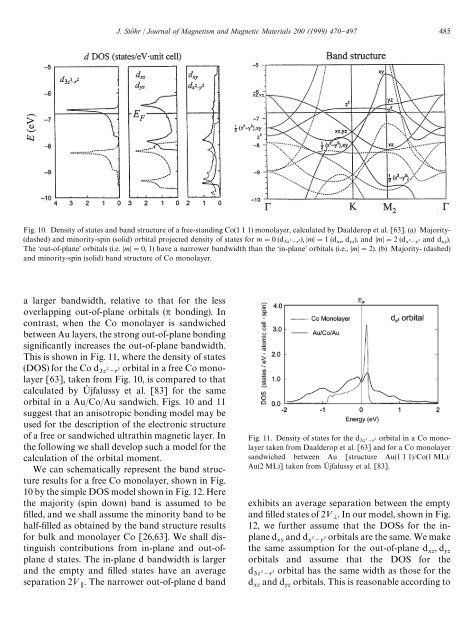
Fig. 10. Density of states and band structure of a free-standing Co(1 1 1) monolayer, calculated by Daalderop et al. [63]. (a) Majority-
(dashed) and minority-spin (solid) orbital projected density of states for m"0(d ), m"1(d ,d ), and m"2(d and d ).
The &out-of-plane' orbitals (i.e. m"0, 1) have a narrower bandwidth than the &in-plane' orbitals (i.e., m"2). (b) Majority- (dashed)
and minority-spin (solid) band structure of Co monolayer.
a larger bandwidth, relative to that for the less
overlapping out-of-plane orbitals ( bonding). In
contrast, when the Co monolayer is sandwiched
between Au layers, the strong out-of-plane bonding
signi"cantly increases the out-of-plane bandwidth.
This is shown in Fig. 11, where the density of states
(DOS) for the Co d orbital in a free Co monolayer
[63], taken from Fig. 10, is compared to that
calculated by UD jfalussy et al. [83] for the same
orbital in a Au/Co/Au sandwich. Figs. 10 and 11
suggest that an anisotropic bonding model may be
used for the description of the electronic structure
of a free or sandwiched ultrathin magnetic layer. In
the following we shall develop such a model for the
calculation of the orbital moment.
We can schematically represent the band structure
results for a free Co monolayer, shown in Fig.
10 by the simple DOS model shown in Fig. 12. Here
the majority (spin down) band is assumed to be
"lled, and we shall assume the minority band to be
half-"lled as obtained by the band structure results
for bulk and monolayer Co [26,63]. We shall distinguish
contributions from in-plane and out-ofplane
d states. The in-plane d bandwidth is larger
and the empty and "lled states have an average
separation 2< , . The narrower out-of-plane d band
Fig. 11. Density of states for the d orbital in a Co monolayer
taken from Daalderop et al. [63] and for a Co monolayer
sandwiched between Au [structure Au(1 1 1)/Co(1 ML)/
Au(2 ML)] taken from UD jfalussy et al. [83].
exhibits an average separation between the empty
and "lled states of 2< . In our model, shown in Fig.
12, we further assume that the DOSs for the inplane
d and d orbitals are the same. We make
the same assumption for the out-of-plane d ,d
orbitals and assume that the DOS for the
d orbital has the same width as those for the
d and d orbitals. This is reasonable according to