Extrasolar Moons as Gravitational Microlenses Christine Liebig

CHAPTER 3. METHOD 21
−∆mag
3
2
1
Triple Lens Binary Lens Difference
0
0.12 0.13 0.14 0.15 0.16 0.17 0.18
t/tE
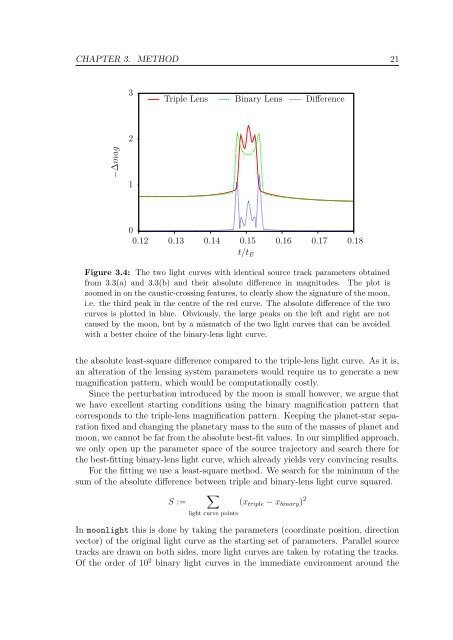
Figure 3.4: The two light curves with identical source track parameters obtained
from 3.3(a) and 3.3(b) and their absolute difference in magnitudes. The plot is
zoomed in on the caustic-crossing features, to clearly show the signature of the moon,
i.e. the third peak in the centre of the red curve. The absolute difference of the two
curves is plotted in blue. Obviously, the large peaks on the left and right are not
caused by the moon, but by a mismatch of the two light curves that can be avoided
with a better choice of the binary-lens light curve.
the absolute least-square difference compared to the triple-lens light curve. As it is,
an alteration of the lensing system parameters would require us to generate a new
magnification pattern, which would be computationally costly.
Since the perturbation introduced by the moon is small however, we argue that
we have excellent starting conditions using the binary magnification pattern that
corresponds to the triple-lens magnification pattern. Keeping the planet-star separation
fixed and changing the planetary mass to the sum of the masses of planet and
moon, we cannot be far from the absolute best-fit values. In our simplified approach,
we only open up the parameter space of the source trajectory and search there for
the best-fitting binary-lens light curve, which already yields very convincing results.
For the fitting we use a least-square method. We search for the minimum of the
sum of the absolute difference between triple and binary-lens light curve squared.
S :=
(xtriple − xbinary) 2
light curve points
In moonlight this is done by taking the parameters (coordinate position, direction
vector) of the original light curve as the starting set of parameters. Parallel source
tracks are drawn on both sides, more light curves are taken by rotating the tracks.
Of the order of 10 2 binary light curves in the immediate environment around the