Experimental and numerical detonation cell in H2-N2O-Ar mixtures

More documents

Recommendations

Info

example of soot record is shown in Figure 1. Soot records are digitised and analysed using the Visilog software. The cell size, λ, reported in the present study corresponds to the mean of the largest and smallest cells measured on a given foil. Figure 1: Experimental soot record of detonation cells in aH2-N2O-Ar mixture. Initial conditions: Φ = 1; XAr = 0.2; P1 =10kPa;T1 = 295 K. Methods The presently used chemical kinetic model, constituted of 203 reactions and 32 species, was previously described and validated against numerous experimental shock-tube, flow reactor and flame speed data [11, 12]. Since it is too large to be directly applied to multidimensional detonation simulations, it has to be reduced to the minimum number of reactions describing the heat release dynamics in the detonation wave. The reduction was conducted using an automatic procedure [13] for the elimination of redundant chemical reactions. This procedure is based on the simulation of an autoignition process in a homogeneous adiabatic constant-pressure reactor. The importance of each reaction is evaluated from an error criterion based on the following macroscopic characteristics of the oxidation process: ignition delay time (time interval to the thermicity peak), maximum thermicity, profiles of temperature and mean molar mass. The errors are determined with respect to the same characteristics obtained with the detailed kinetic model. Reactions are eliminated one after the other, starting from the least important one until none of the remaining reactions can be deleted without exceeding the imposed error tolerances, resulting in a reduced kinetic scheme. For cell size prediction, two methods are used. The first one corresponds to the classical correlation, λ =A.Δi, withΔi, the induction distance and A, the ratio of the cell size to the induction distance. The second one is the use of a 2D Euler code to simulate 2 the detonation wave propagation. Instead of using the A ratio obtained from previous experiments, A is calculated using the Ng’s method, described in details in Refs. [14, 15]. Briefly, A is obtained from the reduced activation energy, ɛi, as defined by Schultz and Shepherd [16], a stability parameter, χ, which corresponds to the ratio of the induction distance to the reaction distance, and fit coefficients. This method allows the use of detailed kinetic schemes within the ”Shock and Detonation Tool Box” from Caltech to determine induction distances. A high-resolution Euler code for a reactive flow, based on the shock-capturing, Weighted Essentially Non-Oscillatory (WENO) scheme of the fifth order [17], is applied to a 2-D detonation simulation. To avoid restrictions on the time step, the time integration is performed with the semi-implicit additive Runge-Kutta scheme ASIRK2C [18]. The convective terms are included in the explicit operator whereas all source terms are treated implicitly. The global time step is controlled by imposing a Courant number equal to 0.7. The code is parallized using MPI library. 2D simulations are made on two rectangular domains whose dimensions are 150 mm in the direction of the detonation propagation and 39 mm or 78 mm in the transversal direction. The computational mesh is structured and orthogonal. In the longitudinal direction, it consists of 500 points uniformly distributed with a step of 50 μm and 500 points with progressively increasing spacing. The detonation front is kept within the first mesh portion. In the transversal direction, the mesh consists of 400 or 800 equally spaced points. To obtain a nearly standing detonation front, a uniform flow at the Chapman-Jouguet (CJ) detonation velocity is imposed on the inlet boundary. CJ conditions are considered on the outlet boundary. Symmetry or perfectly reflecting conditions are imposed on the two remaining boundaries. Results and Discussion Experimental results As a first step, the evolution of wave velocity as a function of the pressure ratio of driver to driven sections (P4/P1) is measured. This ratio (P4/P1) is linked to the shock strength. Stoichiometric mixtures, 50 mol% Ar diluted, at initial pressures of 10 kPa and 20 kPa are used. Figure 2 shows the results obtained at initial pressure of 10 kPa. In the left part of the graph, the velocity of the incident shock increases linearly with (P4/P1) ratio. Then, for a critical ratio around 55, the coupling between the shock wave and the reaction zone
ecomes effective inducing a large jump in the measured velocity. Finally, as the (P4/P1) ratio continues to increase, the wave velocity tends to stabilize at the self-sustained CJ velocity. It can be noted that the critical pressure ratio is significantly reduced at higher initial pressure ((P4/P1)≈35 for P1 = 20 kPa) due to the decrease of the critical energy for detonation onset. Critical conditions for the detonation onset have been estimated at several initial pressures from the ideal 1-D shock wave theory, using the velocity measurements as a function of the (P4/P1) ratio. For P1 =10kPa,the critical temperature and pressure are 904 K and 127 kPa, respectively. For P1 = 20 kPa, the critical temperature is 750 K and the critical pressure is 188 kPa. Wave velocity (m/s) 2400 2000 1600 1200 800 400 Experimental data CJ velocity 20 40 60 80 P 4/P 1 Figure 2: Wave velocity in H2-N2O-Ar mixture as a function of the (P4/P1) ratio. Initial conditions: Φ = 1; XAr =0.5;P1 =10kPa;T1 = 295 K λ (mm) 10 80 70 60 50 40 30 20 X Ar = 0.2 X Ar = 0.4 X Ar = 0.6 1 Equivalence ratio Figure 3: Detonation cell size in H2-N2O-Ar mixtures as a function of equivalence ratio at different dilutions. 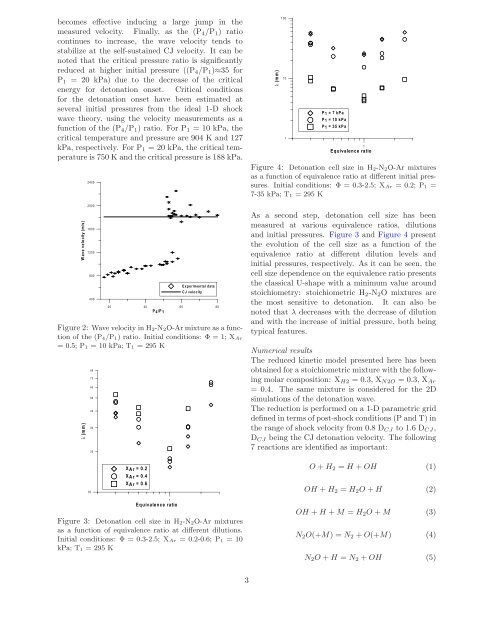Initial conditions: Φ = 0.3-2.5; XAr = 0.2-0.6; P1 =10 kPa; T1 = 295 K 3 λ (mm) 100 10 1 P 1 = 7 kPa P 1 = 10 kPa P 1 = 35 kPa 1 Equivalence ratio Figure 4: Detonation cell size in H2-N2O-Ar mixtures as a function of equivalence ratio at different initial pressures. Initial conditions: Φ = 0.3-2.5; XAr =0.2;P1 = 7-35 kPa; T1 = 295 K As a second step, detonation cell size has been measured at various equivalence ratios, dilutions and initial pressures. Figure 3 and Figure 4 present the evolution of the cell size as a function of the equivalence ratio at different dilution levels and initial pressures, respectively. As it can be seen, the cell size dependence on the equivalence ratio presents the classical U-shape with a minimum value around stoichiometry: stoichiometric H2-N2O mixtures are the most sensitive to detonation. It can also be noted that λ decreases with the decrease of dilution and with the increase of initial pressure, both being typical features. Numerical results The reduced kinetic model presented here has been obtained for a stoichiometric mixture with the following molar composition: XH2 =0.3,XN2O =0.3,XAr = 0.4. The same mixture is considered for the 2D simulations of the detonation wave. The reduction is performed on a 1-D parametric grid defined in terms of post-shock conditions (P and T) in the range of shock velocity from 0.8 DCJ to 1.6 DCJ, DCJ being the CJ detonation velocity. The following 7 reactions are identified as important: O + H2 = H + OH (1) OH + H2 = H2O + H (2) OH + H + M = H2O + M (3) N2O(+M) =N2 + O(+M) (4) N2O + H = N2 + OH (5)
Page 1: Experimental and numerical detonati
Page 5 and 6: a function of the equivalence ratio

Experimental and numerical detonation cell in H2-N2O-Ar mixtures

Create successful ePaper yourself

Delete template?

Save as template?