Undirected graphs and networks

180 General Mathematics
WORKED Example
11
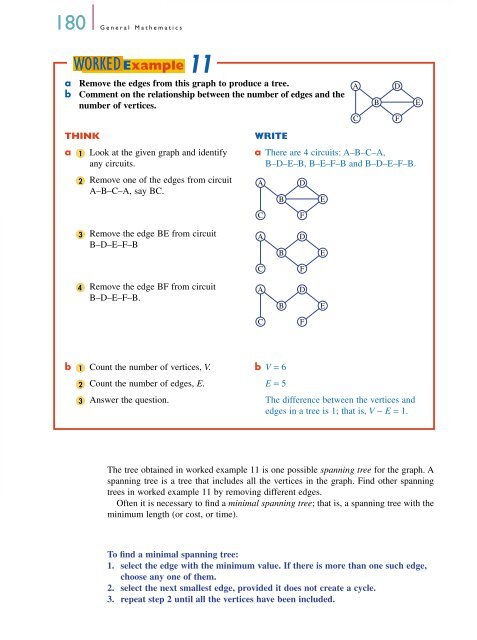
a Remove the edges from this graph to produce a tree.
b Comment on the relationship between the number of edges and the
number of vertices.
THINK WRITE
a 1 Look at the given graph and identify a There are 4 circuits: A–B–C–A,
any circuits.
B–D–E–B, B–E–F–B and B–D–E–F–B.
2 Remove one of the edges from circuit
A–B–C–A, say BC.
A
B
D
E
3 Remove the edge BE from circuit
A
B–D–E–F–B
4 Remove the edge BF from circuit
A
B–D–E–F–B.
b 1 Count the number of vertices, V. b V = 6
2 Count the number of edges, E. E = 5
3 Answer the question. The difference between the vertices and
edges in a tree is 1; that is, V − E = 1.
C
C
C
The tree obtained in worked example 11 is one possible spanning tree for the graph. A
spanning tree is a tree that includes all the vertices in the graph. Find other spanning
trees in worked example 11 by removing different edges.
Often it is necessary to find a minimal spanning tree; that is, a spanning tree with the
minimum length (or cost, or time).
To find a minimal spanning tree:
1. select the edge with the minimum value. If there is more than one such edge,
choose any one of them.
2. select the next smallest edge, provided it does not create a cycle.
3. repeat step 2 until all the vertices have been included.
F
D
B E
F
D
B E
F
A
C
D
B E
F