Lawrence et al., 2012: DRAFT: JGR: Ambient Noise Numerical ...

Lawrence et al., 2012: DRAFT: JGR: Ambient Noise Numerical Evaluation
Figure 4:
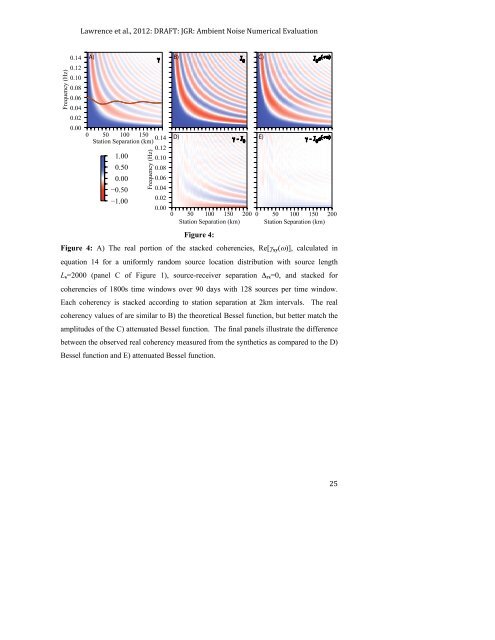
Figure 4: A) The real portion of the stacked coherencies, Re[γxy(ω)], calculated in
equation 14 for a uniformly random source location distribution with source length
Ls=2000 (panel C of Figure 1), source-receiver separation Δrs=0, and stacked for
coherencies of 1800s time windows over 90 days with 128 sources per time window.
Each coherency is stacked according to station separation at 2km intervals. The real
coherency values of are similar to B) the theoretical Bessel function, but better match the
amplitudes of the C) attenuated Bessel function. The final panels illustrate the difference
between the observed real coherency measured from the synthetics as compared to the D)
Bessel function and E) attenuated Bessel function.
25