3. Game Theory - Economic Theory (Prof. Schmidt) - LMU
3. Game Theory - Economic Theory (Prof. Schmidt) - LMU
3. Game Theory - Economic Theory (Prof. Schmidt) - LMU
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
<strong>3.</strong> <strong>Game</strong> <strong>Theory</strong><br />
Klaus M. <strong>Schmidt</strong><br />
<strong>LMU</strong> Munich<br />
Micro (Research), Winter 2011/12<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 1 / 168
Introduction<br />
<strong>Game</strong> theory considers interpersonal or interactive decision making: Two<br />
or more “players” interact with each other and the outcome depends on all of<br />
their decisions.<br />
When a player chooses his action he must form beliefs about what his<br />
opponents are going to do and how his decision may affect the decision of the<br />
other players. This is called strategic interaction.<br />
Discussion: Is there strategic interaction<br />
on perfectly competitive markets?<br />
on oligopolistic markets?<br />
on a monopolistic market?<br />
c○ 2011 Klaus M. <strong>Schmidt</strong><br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 2 / 168
Other Applications of <strong>Game</strong> <strong>Theory</strong><br />
Bargaining: buyer and seller, unions and employers, political parties, etc.<br />
Auctions: Optimal strategies in auctions, optimal design of auctions.<br />
Cooperation in small groups: Provision of public goods, coordination, etc.<br />
Conflicts: strategic interaction in strikes, in war, in tariff wars, etc.<br />
Behavior within and between organisations: Motivation of workers,<br />
control of managers, etc.<br />
Difference between <strong>Game</strong> <strong>Theory</strong> and Contract <strong>Theory</strong><br />
<strong>Game</strong> theory takes the strategic environment as exogenously given.<br />
Contract theory (mechanism design, implementation theory) designs<br />
strategic environment to induce desired behavior.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 3 / 168
Historical Notes<br />
<strong>Game</strong> <strong>Theory</strong> started out as a branch of mathematics (Zermelo 1913,<br />
Borel 1920s)<br />
Analysis of parlor games: Chess, Poker<br />
Focus on zero-sum games<br />
John von Neumann and Oskar Morgenstern (1944), “The <strong>Theory</strong> of<br />
<strong>Game</strong>s and <strong>Economic</strong> Behavior”<br />
Cooperative vs. non-cooperative game theory<br />
John Nash (1951): Nash equilibrium<br />
Reinhard Selten (1967): Subgame perfect equilibrium<br />
John Harsanyi (1969): Bayesian Nash equilibrium<br />
since 1980s widespread applications in all fields of economics<br />
since 1994 many Nobel prizes for game theorists<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 4 / 168
Interpretation of <strong>Game</strong> <strong>Theory</strong><br />
Traditional game theory assumes that all players are perfectly rational and<br />
able to compute and coordinate on an equilibrium of the game. This<br />
assumption is much stronger than in theories of individual decision making.<br />
Normative Interpretation: <strong>Game</strong> theory asks what a perfectly rational player<br />
should do.<br />
What does rationality mean when players interact strategically?<br />
What are rational expectations?<br />
What is an equilibrium?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 5 / 168
Positive Interpretation: <strong>Game</strong> theory tries to explain and to predict behavior<br />
of real people.<br />
Real people are only boundedly rational, i.e. they try to be rational but fail<br />
occasionally.<br />
If people experience a certain strategic situation repeatedly, they<br />
eventually learn to behave rationally and to play the equilibrium of the<br />
game.<br />
Deviations from rational behavior are random and cancel out in the<br />
aggregate.<br />
Experimental economics studies how real people actually behave.<br />
Behavioral economics tries to model this behavior.<br />
The reference point is always the prediction of traditional game theory.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 6 / 168
Literature:<br />
Most of this chapter is based on:<br />
MWG, Chapters 7 - 9<br />
This is required reading!<br />
In addition, it may be useful to consider another textbook covering this<br />
material, e.g.<br />
Kreps (1990) Chapters 11-14<br />
Gibbons (1992) Chapters 1-4<br />
Fudenberg and Tirole (1991), Chapters 1-3, 6, 8.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 7 / 168
<strong>3.</strong>1 Static <strong>Game</strong>s of Complete Information<br />
We start out with games where all players simultaneously have to take a<br />
decision and all players know the structure of the game. To analyze such a<br />
game we have to know:<br />
1) The set of players<br />
I = {1, 2, . . . , n}<br />
2) The set of strategies each player can choose from<br />
Si, i ∈ I, with si ∈ Si<br />
A profile of strategies for all players is a vector<br />
Sometimes we will write:<br />
s = (s1, s2, . . . , sn) ∈ × n i=1Si .<br />
s = (si, s−i) ∈ (Si, S−i) ,<br />
where s−i is the vector of strategies of all other players (except player i)<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 8 / 168
3) The payoff function of each player<br />
ui : S1 × S2 × · · · × Sn → R ,<br />
mapping all possible strategy profiles into payoffs for all players.<br />
Definition <strong>3.</strong>1 (Normal Form)<br />
The normal form of a game G = [I; {Si}; {ui}] consists of<br />
1) the set of players, I = {1, . . . , n},<br />
2) the strategy sets of all players {Si} = {S1, . . . , Sn},<br />
3) the payoff functions of all players {ui} = {u1, . . . , un}.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 9 / 168
The normal form of a two-player game can be expressed and analyzed in a<br />
bimatrix:<br />
2<br />
❅<br />
❅<br />
1<br />
❅<br />
C<br />
D<br />
C D<br />
4, 4 0, 5<br />
5, 0 1, 1<br />
FIG. <strong>3.</strong>1: Normal Form of the Prisoner’s Dilemma <strong>Game</strong> in a Bimatrix<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 10 / 168
Remarks:<br />
What is meant by “simultaneous move”?<br />
Payoffs are assumed to be von Neumann-Morgenstern utilities. What<br />
does this imply if there is uncertainty?<br />
Keep in mind that in the real world payoffs are often monetary payoffs.<br />
What does it imply to treat monetary payoffs as von<br />
Neumann-Morgenstern utilities?<br />
We assume not only that all players know the structure of the game. We<br />
assume in addition that the structure of the game is “common<br />
knowledge”. What does this mean? Why is this important?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 11 / 168
Dominance<br />
Definition <strong>3.</strong>2 (Strictly Dominated Strategy)<br />
A strategy ˆsi of player i is strictly dominated if there exists another strategy<br />
˜si ∈ Si such that ˜si yields a strictly greater payoff than ˆsi no matter what<br />
strategies are chosen by his opponents:<br />
ui(ˆsi, s−i) < ui(˜si, s−i) ∀s−i ∈ S−i .<br />
Are there any beliefs about what the other players will do under which a<br />
rational player would ever choose a strictly dominated strategy?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 12 / 168
Definition <strong>3.</strong>3 (Dominant Strategy)<br />
Strategy s∗ i of player i is a dominant strategy if it strictly dominates all other<br />
strategies of player i, i.e. a dominant strategy is a strictly best response<br />
against all other strategy vectors s−i:<br />
ui(s ∗ i , s−i) > ui(si, s−i) ∀si ∈ Si \ {s ∗ i }, s−i ∈ S−i.<br />
Are there any beliefs about what the other players will do under which a<br />
rational player will not play a dominant strategy?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 13 / 168
Proposition <strong>3.</strong>1 (Equilibrium in Dominant Strategies)<br />
If in G = [I, {Si}; {ui}] each player i has a dominant strategy, and if each<br />
player is rational, then the unique equilibrium is that all players use their<br />
dominant strategies.<br />
Remarks:<br />
How to prove this?<br />
Does this proposition require the assumption of common knowledge?<br />
What does this proposition imply for the prisoner’s dilemma game?<br />
What would you conclude from the observation that many real people do<br />
not play the dominant strategy in the prisoner’s dilemma game?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 14 / 168
Mixed Strategies<br />
So far we considered only pure strategies. However, a player can also<br />
randomize over his available strategies and play a mixed strategy.<br />
Definition <strong>3.</strong>4 (Mixed Strategy)<br />
Consider a normal form game G with finite strategy sets Si = {si1, . . . , siKi }. A<br />
mixed strategy for player i is a probability distribution σi = (σi1, . . . , σiKi ) over<br />
Si, with 0 ≤ σik ≤ 1 for k = 1, . . . , Ki and σi1 + . . . + σiKi = 1.<br />
Remarks:<br />
1) A pure strategy can be seen as the extreme case of a mixed strategy: All<br />
probability mass is put on one strategy.<br />
2) The support of a mixed strategy is the set of all actions that are chosen<br />
with strictly positive probability.<br />
3) The set of all mixed strategies of player i is denoted by ∆(Si).<br />
4) A mixed strategy σi is a best response to the (possibly mixed) strategy<br />
profile σ−i of all other players if and only if each pure strategy in the<br />
support of σi is a best response to σ−i. Why?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 15 / 168
4) A mixed strategy σi can strictly dominate a pure strategy si even if none<br />
of the pure strategies in the support of σi dominate si. Example:<br />
2<br />
❅<br />
❅<br />
1<br />
❅<br />
U<br />
M<br />
D<br />
ℓ r<br />
3, - 0, -<br />
0, - 3, -<br />
1, - 1, -<br />
FIG. <strong>3.</strong>2: A Mixed Strategy Strictly Dominates a Pure Strategy<br />
D is neither dominated by U nor by M, but the mixed strategy ( 1 1<br />
2 , 2 , 0)<br />
strictly dominates D!<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 16 / 168
Best Response<br />
Definition <strong>3.</strong>5 (Best Response)<br />
In game G = [I, {∆(Si)}; {ui}] strategy σi is a best response for player i to<br />
his rivals’ strategies σ−i if<br />
ui(σi, σ−i) ≥ ui(σ ′ i , σ−i)<br />
for all σ ′ i ∈ ∆(Si). Strategy σi is never a best response if there is no σ−i for<br />
which σi is a best response.<br />
Remarks:<br />
1. A “best response” is often called a “best reply”. This is the same thing.<br />
2. If a rational player believes that his opponents play σ−i he wants to play a<br />
best response against σ−i.<br />
<strong>3.</strong> A pure strategy that is not a best response against any pure strategy may<br />
still be a best response against a mixed strategy. Example:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 17 / 168
2<br />
❅<br />
❅<br />
1<br />
❅<br />
U<br />
M<br />
D<br />
L R<br />
3, - 0, -<br />
0, - 3, -<br />
2, - 2, -<br />
FIG. <strong>3.</strong>3: Best Response Against a Mixed Strategy<br />
D is not a best response against L and not a best response against R.<br />
However, if player 2 chooses L with probability 1<br />
1<br />
2 and R with probability 2 ,<br />
then D is a best response of player 1.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 18 / 168
Iterated Elimination of Strictly Dominated Strategies<br />
Which strategies can be eliminated in the following game?<br />
2<br />
❅<br />
❅<br />
1<br />
❅<br />
U<br />
D<br />
L M R<br />
1, 0 1, 2 0, 1<br />
0, 3 0, 1 2, 0<br />
FIG. <strong>3.</strong>4: Iterated Elimination of Strictly Dominated Strategies<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 19 / 168
Remarks:<br />
IESDS requires not only that players are rational, but also that rationality<br />
is common knowledge. Why?<br />
The sequence of elimination of strictly dominated strategies does not<br />
affect the result.<br />
You may also eliminate strategies that are strictly dominated by a mixed<br />
strategy.<br />
But: You are not allowed to eliminate weakly dominated strategies!<br />
In some games IESDS yields a unique equilibrium outcome, e.g. in the<br />
Cournot game or the Beauty Contest.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 20 / 168
Rationalizability<br />
If a rational player believes that his opponents choose strategy profile σ−i then<br />
he should choose a strategy σi that is a best response to σ−i.<br />
This implies that if σi is never a best response, i.e., if there is no strategy σ−i<br />
such that σi is a best response to it, then a rational player should not choose<br />
σi. We say that σi is not rationalizable.<br />
Strategies that are not rationalizable can be eliminated, because all players<br />
know that these strategies will not be used. ⇒ Iterated elimination of<br />
strategies that are never best responses.<br />
Definition <strong>3.</strong>6 (Rationalizability)<br />
In game G = [I, {∆(Si)}; {ui}] the strategies in ∆(Si) that survive the iterated<br />
elimination of strategies that are never best responses are known as player i’s<br />
rationalizable strategies.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 21 / 168
Remarks:<br />
1. Every strategy that is strictly dominated is not rationalizable.<br />
2. The set of rationalizable strategies must be a subset of the set of<br />
strategies that survive IESDS. Why?<br />
<strong>3.</strong> It turns out that in two player games the set of strategies that survive<br />
IESDS and the set of rationalizable strategies coincide.<br />
4. However, in games with more than two players there can be strategies<br />
that are never a best response and yet are not strictly dominated.<br />
5. If a strategy σi is “rationalizable” then player i can tell a coherent story<br />
why he uses σi. Example:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 22 / 168
2<br />
1 ❅<br />
❅<br />
a1<br />
a2<br />
a3<br />
a4<br />
b1 b2 b3 b4<br />
0, 7 2, 5 7, 0 0, 1<br />
5, 2 3, 3 5, 2 0, 1<br />
7, 0 2, 5 0, 7 0, 1<br />
0, 0 0, -2 0, 0 10, -3<br />
FIG. <strong>3.</strong>5: Rationalizable Strategies<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 23 / 168
4 and a4 can be eliminated.<br />
All other strategies are rationalizable. Consider e.g. a1. Player 1 can<br />
rationalize a1 by pointing to the following chain of arguments:<br />
(a1, b3, a3, b1, a1, b3, a3, b1, . . .).<br />
How can player 2 rationalize b2?<br />
Is it possible to rationalize a4?<br />
Suppose B’s payoff at (a4, b4) is not −3 but +1. Is it now possible to<br />
rationalize a4?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 24 / 168
Nash Equilibrium<br />
In many games there are many rationalizable strategies. Which strategies<br />
should we expect to be played?<br />
John Nash’s answer to this question is that strategies should form an<br />
equilibrium in the sense that each player plays a best response to the<br />
strategies chosen by all other players, so nobody has an incentive to deviate<br />
from this strategy profile.<br />
Definition <strong>3.</strong>7 (Nash Equilibrium)<br />
A strategy profile s = (s1, . . . , sI) is a Nash Equilibrium (NE) of game<br />
G = [I, {Si}, {ui(·)}] if for every i ∈ {1, . . . , I}<br />
for all s ′ i<br />
∈ Si.<br />
ui(si, s−i) ≥ ui(s ′ i , s−i)<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 25 / 168
Remarks:<br />
1. Nash Equilibrium requires that the strategy of each player is a best<br />
response against the actual strategies chosen by all other players. In<br />
contrast, rationalizability only requires that a strategy is a best response<br />
to a profile of rationalizable strategies of his opponents.<br />
2. Thus, Nash Equlibrium requires not only that players play a best<br />
response against the strategies of their opponents. It also requires that<br />
players form correct expectations about the strategies that the other<br />
players are going to choose. It is the second requirement that is<br />
particularly demanding.<br />
<strong>3.</strong> We only require a weak inequality. If a strict inequality holds we have a<br />
“Strict Nash Equilibrium”. However, in many games a Strict Nash<br />
Equilibrium does not exist.<br />
4. Nash Equilibrium strategies must be rationalizable, they cannot be strictly<br />
dominated, but they may be weakly dominated. Why?<br />
5. We only require that unilateral deviations from the proposed strategy<br />
profile are not profitable. We do not require that a coordinated deviation<br />
of several players is unprofitable. This is why this is called<br />
“non-cooperative” game theory.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 26 / 168
How to find a Nash Equilibrium<br />
In a two-player game with a finite number of strategies it is easy to find all<br />
Nash equilibria:<br />
Consider each strategy of player 2 and mark the best responses of player<br />
1 by underlining his highest payoffs in column.<br />
Consider each strategy of player 1 and mark the best responses of player<br />
2 by underlining her highest payoffs in each row.<br />
Those cells in which both payoffs are underlined constitute a pair of<br />
mutually best responses, i.e. a Nash Equilibrium.<br />
With more than two players you have to systematically go through all<br />
possibilities. If the game is symmetric, try to exploit this in order to reduce the<br />
number of cases.<br />
If strategy spaces are continuous, look at the first order conditions in order to<br />
find “best response correspondences”. Don’t forget to check the second order<br />
conditions.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 27 / 168
2<br />
1 ❅<br />
❅<br />
a1<br />
a2<br />
a3<br />
a4<br />
b1 b2 b3 b4<br />
0, 7 2, 5 7, 0 0, 1<br />
5, 2 3, 3 5, 2 0, 1<br />
7, 0 2, 5 0, 7 0, 1<br />
0, 0 0, -2 0, 0 10, -3<br />
FIG. <strong>3.</strong>6: Nash Equilibrium<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 28 / 168
2<br />
❅<br />
❅ Marienplatz University<br />
1<br />
❅<br />
Marienplatz<br />
University<br />
10, 10 0, 0<br />
0, 0 10, 10<br />
FIG. <strong>3.</strong>7: Meet you in Munich<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 29 / 168
Why should we expect real players to play a Nash Equilibrium?<br />
1. NE as an implication of rationality and common knowledge of<br />
rationality<br />
This argument is not correct! A rational player must play a rationalizable<br />
strategy, but rationality does not imply that his forecast of what other<br />
players are going to do is correct.<br />
2. NE as an implication of consistency<br />
If rationality is common knowledge, each player knows that each player<br />
will play a best response to what he beliefs what the other players will do.<br />
Only NE are strategy combinations at which all players play best<br />
responses to their beliefs and all beliefs are correct. If any other strategy<br />
combination was played, then at least one player must make a mistake by<br />
either choosing the wrong strategy given his belief or by having a belief<br />
that is mistaken. Thus, if there is a unique NE, then this is the only<br />
consistent way how the game can be played. But if there are multiple NE,<br />
players somehow have to coordinate on which equilibrium to play.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 30 / 168
<strong>3.</strong> NE as a self-enforcing agreement<br />
Suppose that players can talk about which strategies to play before the<br />
game starts. Would they ever agree to play a strategy profile that is not a<br />
NE? If there are multiple NE and players agree to play one of them, then<br />
nobody has an incentive to deviate from this agreement. Agreeing to play<br />
a NE is a self-enforcing agreement.<br />
4. NE as a focal point<br />
Even if there are multiple equilibria it is sometimes “obvious” which<br />
equilibrium will be played. Reasons for “obviousness” can be efficiency,<br />
symmetry, or a joint cultural background. See Schelling (1960) for many<br />
fun examples.<br />
5. NE as a stable social norm or convention<br />
There are many social conventions or norms that select one out of many<br />
possible NE, e.g. “Drive/Walk on the right side of the street/sidewalk”,<br />
“Ladies first”, “share equally”, etc.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 31 / 168
6. NE as a stable outcome of a learning or an evolutionary process<br />
If players play a game very often they will eventually learn to play a Nash<br />
Equilibrium. Similarly, evolution will shape “strategies” of plants and<br />
animals such that they are best responses to each other. To make these<br />
arguments precise we have to specify the learning/evolutionary process<br />
explicitly. But many of these processes converge to NE.<br />
Whether players play a Nash equilibriium is an empirical question. The<br />
experimental evidence suggests that real players are more likely to play a<br />
Nash Equilibrium the more experience they have with the game (Discussion:<br />
beauty contest). Furthermore, it helps if the Nash equilibrium is unique or if<br />
there is one NE that is the obvious focal point.<br />
If you play a game against somebody who is inexperienced and whom you<br />
expect not to play his NE stragegy, then you should typically not choose your<br />
NE stragegy either!<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 32 / 168
Proposition <strong>3.</strong>2<br />
If the strategy profile (s∗ 1 , . . . , s∗ n) is a NE, then all s∗ i , i = 1, . . . , n, must<br />
survive the iterated elimination of strictly dominated strategies.<br />
Proof:(by contradiction) Suppose that some s∗ i do not survive IESDS. Let j be<br />
the first player whose equilibrium strategy s∗ i is going to be eliminated. Then<br />
there exists a strategy ˆsj such that<br />
uj(s ∗ j , s−j) < uj(ˆsj, s−j)<br />
for all s−j that have not yet been eliminated. In particular we must have<br />
uj(s ∗ j , s ∗ −j) < uj(ˆsj, s ∗ −j).<br />
But this is a contradiction to the assumption that (s ∗ 1 , . . . , s∗ n) is a NE. Q.E.D.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 33 / 168
Proposition <strong>3.</strong>3<br />
If G is a finite game and IESDS yields a unique strategy profile (s ∗ 1 , . . . , s∗ n)<br />
then this strategy profile is the unique NE of the game.<br />
Proof: Suppose that (s ∗ 1 , . . . , s∗ n) ist not a NE. Then there exists a player i and<br />
a strategy ˆsi such that<br />
ui(s ∗ i , s ∗ −i) < ui(ˆsi, s ∗ −i).<br />
This ˆsi has been eliminated in the process of IESDS. Thus, there exists an s ′ i<br />
such that ui(ˆsi, s ∗ −i ) < ui(s ′ i , s∗ −i ).<br />
Either s ′ i = s∗ i , then we have found a contradiction already.<br />
Or s ′ i = s∗ i , but then there exists a strategy s′′<br />
i that dominates s ′ i on some<br />
earlier stage of IESDS.<br />
◮ Either s ′′<br />
i = s ∗ i ⇒ contradiction<br />
◮ Or s ′′<br />
i = s ∗ i ⇒ s ′′′<br />
i<br />
Because the set of strategies is finite we must eventually get at a<br />
contradiction.<br />
Uniqueness is implied by Proposition <strong>3.</strong>2. Why? Q.E.D.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 34 / 168
Mixed Strategy Equlibria<br />
2<br />
❅<br />
❅<br />
1<br />
❅<br />
Heads<br />
Tails<br />
What is the NE of this game?<br />
Heads Tails<br />
1, -1 -1, 1<br />
-1, 1 1, -1<br />
FIG. <strong>3.</strong>8: Matching Pennies<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 35 / 168
Definition <strong>3.</strong>8 (Mixed Strategy Equilibrium)<br />
A mixed strategy profile σ = (σ1, . . . , σI) is a NE of game<br />
G = [I, {∆(Si)}, {ui(·)}] if for every i = 1, . . . , I,<br />
for all σ ′ i ∈ ∆(Si).<br />
ui(σi, σ−i) ≥ ui(σ ′ i , σ−i)<br />
Remark: If a player chooses a mixed strategy σi in equilibrium, then all pure<br />
strategies si in the support of σi must yield the same expected payoff which is<br />
greater or equal than the expected payoff of any strategy that is not in the<br />
support of σi. Why?<br />
Proposition <strong>3.</strong>4<br />
In Matching Pennies the unique NE is that both players choose “Heads” with<br />
probability 1/2.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 36 / 168
Proof of Proposition <strong>3.</strong>4:<br />
Let p ∈ [0, 1] denote the probability with which player 1 chooses “Heads” and<br />
q ∈ [0, 1] the probability that player 2 chooses “Heads”. Suppose player 1<br />
chooses “Heads”. Then his expected payoff is:<br />
u1(H) = q · 1 − (1 − q) · 1 = 2q − 1<br />
Suppose player 1 chooses “Tails”. Then his expected payoff is:<br />
⇒ Player 1 should choose “Heads” iff<br />
u1(T ) = −q · 1 + (1 − q) · 1 = 1 − 2q<br />
2q − 1 ≥ 1 − 2q ⇔ q ≥ 1<br />
2<br />
If q = 1<br />
2 player 1 is just indifferent between his two strategies.<br />
Similarly we get for player 2: She should choose “Heads” iff p ≤ 1<br />
2 and she is<br />
just indifferent between “Heads” and “Tails” if p = 1<br />
2 . Q.E.D.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 37 / 168
q<br />
.... .. ..<br />
.. .<br />
..<br />
FIG. <strong>3.</strong>9: Best Response Correspondences for Matching Pennies<br />
There is a unique intersection at p = q = 1<br />
2 . This is a pair of mutual best<br />
responses.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 38 / 168<br />
p
Finding all Nash Equilibria<br />
2<br />
❅1<br />
❅<br />
Bo<br />
Ba<br />
Bo Ba<br />
X1, X2<br />
0, 0<br />
0, 0 Y1, Y2<br />
p<br />
.. .<br />
.. .. ..<br />
q<br />
FIG. <strong>3.</strong>10: All NE in the “Battle of the Sexes”<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 39 / 168
Let p denote the probability that player 1 chooses “Boxing” and q the<br />
probability that player 2 chooses “Ballet”.<br />
Similarly:<br />
u1(Bo) = q · X1 + (1 − q) · 0 = qX1<br />
u1(Ba) = q · 0 + (1 − q) · Y1 = (1 − q)Y1<br />
u1(Bo) ≥ u1(Ba) ⇔ qX1 ≥ (1 − q)Y1 ⇔ q ≥<br />
u2(Bo) ≥ u2(Ba) ⇔ pX2 ≥ (1 − p)Y2 ⇔ p ≥<br />
Hence, there are three NE:<br />
two pure strategy equlibria: (0,0) and (1,1)<br />
one mixed strategy equilibrium:<br />
Y2<br />
X2+Y2 ,<br />
Y1<br />
X1+Y1<br />
<br />
.<br />
Y1<br />
X1 + Y1<br />
Y2<br />
X2 + Y2<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 40 / 168
Remarks:<br />
1) The two pure strategy equilibria are also mixed strategy equilibria with<br />
degenerate probabilities.<br />
2) In the mixed strategy equilibrium player 1 chooses “Boxing” with<br />
probability p∗ = Y2 and player 2 chooses “Boxing’ with probability<br />
X2+Y2<br />
q∗ = Y1<br />
X1+Y1 . Note that p∗ is independent of the payoffs X1, Y1 of player 1.<br />
If X1 increases, player 1 will not go to “Boxing” with a higher probability in<br />
equilibrium. Why not?<br />
p ∗ depends only on the payoffs X2, Y2 of player 2. Each player chooses<br />
his probabilities so as to keep the other player indifferent!<br />
3) It is possible to show that if generic games have a finite number of<br />
equilibria, then this number must be odd! Thus, if you find an even<br />
number of NE you must be missing at least one!<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 41 / 168
Interpretation of Mixed Strategy Equilibria<br />
In a mixed strategy equilibrium a player is indifferent between all pure<br />
strategies in the support of his mixed equilibrium strategy. The probabilities<br />
are chosen so as to keep the other player indifferent. Why should a player<br />
take the trouble and do this?<br />
1) Experienced players do randomize properly (e.g. in soccer or baseball).<br />
2) If a player does not randomize properly, his opponent will eventually<br />
exploit him (if there is repeated interaction).<br />
3) Play “Stone, Paper, Scissors” with a friend many times in a row. Figure<br />
out by introspection whether you randomize.<br />
4) Harsanyi offered an interesting interpretation of a mixed strategy<br />
equilibrium. He assumes that there is incomplete information about the<br />
payoff function of each player. Each player chooses a pure strategy that<br />
depends on his “type”. The mixed strategy equilibrium is the limit of a<br />
sequence of pure strategy equilibria with incomplete information when<br />
the incompleteness of information goes to 0. We will discuss this in more<br />
detail when we get to games with incomplete information.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 42 / 168
Existence of Nash equilibria<br />
John Nash (1951) has shown that a Nash equilibrium exists under fairly weak<br />
conditions.<br />
Proposition <strong>3.</strong>5 (Existence I)<br />
Every normal form game with a finite number of players and finite strategy<br />
spaces has at least one NE, possibly in mixed strategies.<br />
Proposition <strong>3.</strong>6 (Existence II)<br />
Consider a normal form game G = [I, {Si}, {ui(·)}] with strategy sets Si that<br />
are non-empty, compact and subsets of some Euclidean space R M .<br />
(a) If ui(·) is continuous in s for all i = 1, . . . , I then a NE in pure or mixed<br />
strategies exists.<br />
(b) If in addition strategy spaces Si are convex and payoff functions ui(·) are<br />
quasiconcave in s for all i = 1, . . . then there exists a pure strategy NE.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 43 / 168
Remarks:<br />
1) Nash equilibria exist for a large class of games.<br />
2) Even if payoff functions are discontinuous there do exist mixed strategy<br />
NE in many cases (see Dasgubpta and Maskin, 1986).<br />
3) Existence is important:<br />
a) If we don’t know whether a NE exists, it does not make sense to characterize<br />
the properties of all NE.<br />
b) If NE did not exist in naturally defined games, then something was wrong<br />
with our notion of rationality and equilibrium. How should a rational individual<br />
behave, if there is no consistent way how to do so?W<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 44 / 168
Outline of the proof of Proposition <strong>3.</strong>5:<br />
The proof uses a fixed point argument. To illustrate this type of argument<br />
consider Brower’s fixed point theorem first:<br />
Proposition <strong>3.</strong>7 (Brouwer)<br />
Let A ⊂ R N be a non empty, compact and convex set and f : A → A be a<br />
continuous function mapping A into A. Then f has a fixed point, i.e. there<br />
exists an x such that f (x) = x.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 45 / 168
..<br />
..<br />
..<br />
<br />
.. <br />
.<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
1<br />
..<br />
...<br />
..<br />
.<br />
0<br />
1<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
1<br />
0<br />
1<br />
FIG. <strong>3.</strong>11: Brouwer’s Fixed Point Theorem<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 46 / 168
Definition <strong>3.</strong>9 (Upper Hemicontinuity)<br />
Let A ⊂ R N and the compact set Y ⊂ R K . A correspondence f : A → Y is<br />
upper hemicontinuous (uhc) if it has a closed graph.<br />
Proposition <strong>3.</strong>8 (Kakutani)<br />
Supose that A ⊂ R N is a nonempty, compact and convex set and f : A → A is<br />
an upper hemicontinuous correspondence mapping A to A with the property<br />
that the set f (x) ⊂ A is nonempty and convex for every x ∈ A ist. Then f (·)<br />
has a fixed point, i.e., there exists an x ∈ A such that x ∈ f (x).<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 47 / 168
..<br />
..<br />
..<br />
<br />
.. <br />
.<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
1<br />
..<br />
...<br />
..<br />
.<br />
0<br />
1<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
<br />
1<br />
0<br />
1<br />
FIG. <strong>3.</strong>12: Kakutani’s Fixed Point Theorem<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 48 / 168
We now outline the proof of Proposition <strong>3.</strong>5.<br />
Let σi be a mixed strategy of player i and Σi the set of all mixed strategies.<br />
Note that Σi is a nonempty, compact and convex subset of R K , where K is the<br />
number of pure strategies of player i.<br />
Define the best response correspondence<br />
for player i:<br />
Bi : Σ−i → Σi<br />
Bi(σ−i) = arg max ui(σi, σ−i).<br />
σi<br />
It is possible to show that this correspondence is uhc and that Bi(σ−i) is<br />
nonempty and convex for all σ−i ∈ Σ−i.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 49 / 168
Consider now the correspondence B : Σ → Σ defined by:<br />
B(σ1, . . . , σn) = B1(σ−1) × · · · × Bn(σ−n)<br />
This correspondence assigns to every possible strategy profile the best<br />
responses to this strategy profile. A fixed point of this correspondence is a<br />
strategy profile with the property that every strategy in this profile is a best<br />
response to all other strategies in this profile, i.e., it is a Nash Equilibrium.<br />
Thus, we only have to show that the correspondence B has a fixed point. We<br />
can do this by using Kakutani’s fixed point theorem. The conditions of<br />
Kakutani are satisfied<br />
⇒ a fixed point exists<br />
⇒ a Nash Equilibrium exists. Q.E.D.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 50 / 168
<strong>3.</strong>2 Dynamic <strong>Game</strong>s of of Complete Information<br />
So far we looked at games where all players choose their strategies<br />
simultaneously and act only once. These games are best described by their<br />
normal form.<br />
Now we want to look at games that have a more complicated time and<br />
information structure. In a dynamic game players may act sequentially, they<br />
may act several times, and their information may depend on what has<br />
happened in the past. In order to capture this, we have to introduce the<br />
extensive form of a game.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 51 / 168
Definition <strong>3.</strong>10 (Extensive Form)<br />
The extensive form of a game describes:<br />
(1) the set of players, {1, . . . , I};<br />
(2a) at which point in time which player is called to move;<br />
(2b) which actions are feasible for the player when he is called to<br />
move;<br />
(2c) what a player knows about the previous history of the game<br />
when he is called to move;<br />
(3) the payoff of each player as a function of all possible final<br />
histories of the game.<br />
The definition of the extensive form is similar to the definition of the normal<br />
form, but the strategy spaces can be much more complicated.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 52 / 168
In many cases the extensive form of a game can be depicted nicely by a<br />
game tree.<br />
A game tree consists of a set of ordered nodes that are linked to each other.<br />
There are<br />
Decision nodes, at which exactly one player has to choose an action out<br />
of set of feasible actions. Each action leads to new decision or end node.<br />
End nodes, at which the game ends and payoffs are made.<br />
The game tree begins with exactly one initial node.<br />
Each node (except for the initial node) has exactly one predecessor.<br />
Each decision node has at least one successor. An end node does not<br />
have any successors.<br />
A predecessor of node x cannot also be a successor of node x.<br />
For each decision node or end node there exists a unique sequence of<br />
decision nodes linking it to the initial node. Such a sequence of decision<br />
nodes is called the history of the game played up to this node.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 53 / 168
player 2<br />
. .<br />
player 1<br />
.<br />
<br />
action 1 action 2<br />
. .<br />
player 2<br />
action 3 action 4 action 3 action 4<br />
a<br />
b<br />
c<br />
d<br />
e<br />
f<br />
FIG. <strong>3.</strong>13: A <strong>Game</strong> Tree<br />
g<br />
h<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 54 / 168
Exogenous Uncertainty<br />
In many games there is some exogenous uncertainty. For example, an entrant<br />
has to decide whether to enter the market or not. If he enters there are two<br />
possibilities. With 50 percent probability demand is strong and with 50 percent<br />
probability demand is weak.<br />
This can be modeled by introducing Nature as an additional, non-strategic<br />
player. When nature is called to move she determines the state of the world<br />
with the exogenously given probabilities.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 55 / 168
0<br />
2<br />
Entrant<br />
.<br />
.<br />
N E<br />
1<br />
1<br />
Monopolist<br />
2<br />
. .<br />
2<br />
Monopolist<br />
. .<br />
. .<br />
Nature<br />
f n f n<br />
0<br />
0<br />
3<br />
3<br />
−1<br />
−1<br />
<br />
1<br />
1<br />
FIG. <strong>3.</strong>14: A Market Entry <strong>Game</strong> with Exogenous Uncertainty<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 56 / 168
Information Sets<br />
It may happen that a player does not observe all previous moves (of other<br />
players and/or of nature). This can be described by using information sets.<br />
Definition <strong>3.</strong>11 (Information Set)<br />
An information set for a player is a collection of decision nodes satisfying:<br />
(i) the player has to move at every node in the information set, and<br />
(ii) the player does not know which point of the information set he has<br />
reached.<br />
This definition requires that the set of feasible actions the player can choose<br />
from is the same at each node of his information set. Why?<br />
The definition also implies that each decision node belongs to exactly one<br />
information set. Why?<br />
If the decision maker knows at which decision node in the game tree he is,<br />
then this decision node belongs to an information set that is a singleton.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 57 / 168
Examples:<br />
1<br />
1<br />
2<br />
.<br />
.<br />
D C<br />
5<br />
0<br />
1<br />
.<br />
<br />
D C<br />
0<br />
5<br />
. .<br />
2<br />
D C<br />
<br />
4<br />
4<br />
FIG. <strong>3.</strong>15: Prisoner’s Dilemma in Extensive Form<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 58 / 168
1<br />
.<br />
<br />
2<br />
.<br />
.<br />
2<br />
. .<br />
1<br />
. .<br />
1<br />
. .<br />
1<br />
. <br />
1<br />
. .<br />
FIG. <strong>3.</strong>16A: Possible and Impossible Information Sets<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 59 / 168
1<br />
.<br />
<br />
2<br />
.<br />
.<br />
2<br />
. .<br />
1<br />
. .<br />
1<br />
. .<br />
1<br />
. <br />
1<br />
. .<br />
FIG. <strong>3.</strong>16B: Possible and Impossible Information Sets<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 60 / 168
1<br />
.<br />
<br />
2<br />
.<br />
.<br />
2<br />
. .<br />
1<br />
. .<br />
1<br />
. .<br />
1<br />
. <br />
1<br />
. .<br />
FIG. <strong>3.</strong>16C: Possible and Impossible Information Sets<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 61 / 168
<strong>Game</strong>s of Perfect and Imperfect Information<br />
Definition <strong>3.</strong>12 (Perfect Information)<br />
A game is one of perfect information if each information set contains a<br />
single decision node. Otherwise it is a game of imperfect information.<br />
Note:<br />
We will see shortly that finite games of perfect information are particularly<br />
simple to solve.<br />
If players move simultaneously then the game has imperfect information.<br />
If a player does not observe the entire previous history of play the game<br />
is also of imperfect information.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 62 / 168
Strategies in Extensive Form <strong>Game</strong>s<br />
In a static game there is no difference between an action and a strategy.<br />
In a dynamic game, however, a strategy can be much more complex than an<br />
action.<br />
Definition <strong>3.</strong>13 (Strategy)<br />
Let Hi denote the collection of player i’s information sets, A the set of possible<br />
actions in the game, and C(Hi) ⊂ A the set of actions possible at information<br />
set H ∈ Hi. A strategy of player i is a function si : H → A such that<br />
si(H) ∈ C(H) for all H ∈ Hi.<br />
In words: A strategy is a complete contingent plan of actions, i.e., for every<br />
possible contingence (every possible information) a strategy must specify<br />
what the player is going to do.<br />
Note: It is extremely important that the strategy is completely specified. For<br />
example, it is often the case that some information sets cannot be reached if<br />
the player follows a particular strategy. Nevertheless, his strategy has to<br />
specify what the agent would do if these information sets were reached!<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 63 / 168
Examples:<br />
3<br />
1<br />
2<br />
.<br />
.<br />
ℓ r<br />
1<br />
2<br />
1<br />
.<br />
<br />
L R<br />
2<br />
1<br />
. .<br />
2<br />
ℓ r<br />
<br />
0<br />
0<br />
FIG. <strong>3.</strong>17: Strategies in a <strong>Game</strong> with Perfect Information<br />
Player 1 has 2 strategies in this game: L, R<br />
Player 2 has 4 strategies: ℓℓ, ℓr, rℓ, rr<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 64 / 168
2<br />
❅<br />
❅<br />
1<br />
❅<br />
L<br />
R<br />
ℓℓ ℓr rℓ rr<br />
3, 1 3, 1 1, 2 1, 2<br />
2, 1 0, 0 2, 1 0, 0<br />
FIG. <strong>3.</strong>18: Normal Form of this <strong>Game</strong><br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 65 / 168
1<br />
.<br />
<br />
L R<br />
2<br />
.<br />
.<br />
2<br />
. .<br />
ℓ r<br />
ℓ r<br />
1<br />
. .<br />
1<br />
. .<br />
1<br />
. <br />
1<br />
. .<br />
L ′ R ′ L ′ R ′ L ′′ R ′′ L ′′ R ′′<br />
FIG. <strong>3.</strong>19: Strategies in a <strong>Game</strong> with Imperfect Information<br />
Strategies of player 1:<br />
Strategies of player 2:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 66 / 168
Remarks:<br />
Every game in extensive form can be transformed into a game in normal<br />
form.<br />
But: For a given game in normal form there may be several games in<br />
extensive form. Example?<br />
Which form of a game contains more information?<br />
If a game has several stages, the number of strategies grows very rapidly.<br />
Consider for example the following game with perfect information:<br />
◮ At stage 1 player 1 chooses between L and R<br />
◮ At stage 2 player 2 chooses between l and r<br />
◮ At stage 3 player 1 chooses between L and R<br />
◮ at stage 4 player 2 chooses between l and r<br />
How many stragegies does player 1 have?<br />
How many strategies does player 2 have?<br />
What if we add identical stages 5 and 6?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 67 / 168
Backward Induction<br />
<br />
0<br />
2<br />
Entrant<br />
.<br />
<br />
N E<br />
f<br />
−1<br />
−1<br />
. .<br />
Incumbent<br />
a<br />
<br />
2<br />
1<br />
FIG. <strong>3.</strong>20: A Market Entry <strong>Game</strong><br />
The entrant decides whether to enter (E) the market or not (N).<br />
If there is entry the incumbent decides whether to fight (f ) or to<br />
accommodate entry(a).<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 68 / 168
A sequential game with finitely many stages is solved by backward<br />
induction:<br />
Incumbent: Given that the entrant entered the market, what is the optimal<br />
strategy for the incumbent? Accommodate.<br />
Entrant: The entrant anticipates that if he enters the incumbent will<br />
accommodate. Therefore, she should enter.<br />
Backward Induction and Nash Equilibrium<br />
The result of backward induction is a Nash Equilibrium:<br />
Given that the entrant enters it is optimal for the incumbent to<br />
accommodate.<br />
Given that the incumbent accommodates, it is optimal for the entrant to<br />
enter.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 69 / 168
I<br />
❅<br />
❅<br />
E<br />
❅<br />
N<br />
E<br />
f<br />
a<br />
0, 2 0, 2<br />
-1, -1 2, 1<br />
FIG. <strong>3.</strong>21: Normal Form of the Entry <strong>Game</strong><br />
The analysis of the normal form shows that there are two Nash equilibria:<br />
(E, a)<br />
(N, f )<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 70 / 168
Remarks:<br />
(N, f ) is a NE: Given that the incumbent fights it is optimal for the entrant<br />
to stay out. Given that there is no entry it is optimal for the incumbent to<br />
threaten to fight.<br />
If there was entry it would be suboptimal for the incumbent to carry out<br />
his threat of fighting. However, this does not happen in equilibrium (it is a<br />
zero probability event). Therefore, the strategy “fight” is optimal.<br />
However, the second NE is not convincing. It relies on a threat that is not<br />
credible if the incumbent is called to carry it out.<br />
Note that the normal form of the game does not show whether a threat is<br />
credible or not. However, if we look at the extensive form and solve the<br />
game by backward induction then all incredible threats are automatically<br />
eliminated.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 71 / 168
Equilibrium Refinements<br />
In dynamic games there are often many NE. However, we have seen that not<br />
all NE are equally convincing. Some NE are supported by threats that are not<br />
credible, while other NE do not require such threats.<br />
In the following we want to refine the notion of Nash Equilibrium. We will<br />
impose additional desirable conditions that a “good” NE should satisfy. These<br />
“good” NE are given special names, such as “Subgame Perfect Nash<br />
Equilibrium”, “Perfect Equilibrium”, “Perfect Bayesian Equilibrium” etc.<br />
Note:<br />
Even if a NE is not convincing, it is still a NE.<br />
We have to be careful not to require too much. If we impose too strong<br />
conditions, then it may be that many games do not have a NE satisfying<br />
this requirement.<br />
Example: A natural and plausible requirement is that a player should not<br />
use a weakly dominated strategy. However, this condition turns out to be<br />
so strong that in some games the only NE is in weakly dominated<br />
strategies. If we would impose this condition, no equilibrium would be left.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 72 / 168
Subgame Perfect Equilibria<br />
Definition <strong>3.</strong>14 (Subgame)<br />
A subgame of an extensive form game is a subset of the game with the<br />
following properties:<br />
a) It begins with an information set containing a single decision node,<br />
contains all the decision nodes that are successors (both immediate and<br />
later) of this node, and contains only these nodes<br />
b) If decision node x is in the subgame, then every decision node x ′ that is<br />
in the same information set as x is also in the subgame (i.e., there are no<br />
broken information sets).<br />
Note:<br />
The game is a whole is a subgame of itself. Therefore, every game has at<br />
least one subgame.<br />
Whether a dynamic game has only one or several subgames depends on<br />
the information structure.<br />
A subgame is a game in its own right that can be analyzed independently<br />
of the rest of the game.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 73 / 168
1<br />
.<br />
<br />
L R<br />
2<br />
.<br />
.<br />
2<br />
. .<br />
ℓ r<br />
ℓ r<br />
1<br />
. .<br />
1<br />
. .<br />
1<br />
. <br />
1<br />
. .<br />
L ′ R ′ L ′ R ′ L ′′ R ′′ L ′′ R ′′<br />
FIG. <strong>3.</strong>22: Subgames<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 74 / 168
The following definition is due to Reinhard Selten (1965).<br />
Definition <strong>3.</strong>15 (Subgame Perfect Nash Equilibrium)<br />
A Nash Equilibrium of an extensive form game is called a Subgame Perfect<br />
Nash Equilibrium (SPNE) if it induces a Nash Equilibrium in every subgame of<br />
the game.<br />
Remarks:<br />
Subgame Perfection is more general than backward induction. It can also<br />
be applied if the game has simultaneous moves at some stages or if the<br />
game has infinitely many stages.<br />
If the only subgame of a game is the game itself, then every NE is a<br />
SPNE. Why?<br />
A “proper subgame” is a subgame that is not identical with the game<br />
itself.<br />
A SPNE induces a SPNE in every subgame of the game. Why?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 75 / 168
3<br />
1<br />
2<br />
.<br />
✈.<br />
ℓ r<br />
1<br />
2<br />
1<br />
.<br />
✈<br />
L R<br />
2<br />
1<br />
. ✈.<br />
2<br />
ℓ r<br />
<br />
0<br />
0<br />
FIG. <strong>3.</strong>23: Subgame Perfect Nash Equilibrium<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 76 / 168
Remarks:<br />
The equilibrium path is (R, l)<br />
But: The equilibrium has to specify also what happens off the equilibrium<br />
path. Therefore, the SPNE is (R, rl).<br />
There exists a second NE: (L, rr). But this NE is not subgame perfect. It<br />
is based on the incredible threat that player 2 chooses r if player 1<br />
chooses R.<br />
SPNE are well defined for games with perfect and with imperfect<br />
information. However, if the game has imperfect information, it may be<br />
that it does not have any proper subgame.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 77 / 168
Proposition <strong>3.</strong>9 (Existence and Uniqueness)<br />
(a) Every finite game of perfect information has at least one pure strategy<br />
SPNE.<br />
(b) If no player has the same payoffs at any two terminal nodes, then there is<br />
a unique SPNE.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 78 / 168
Proof: The proof of part (a) is by construction and uses the generalized<br />
backward induction procedure:<br />
(1) Start at the end of the game tree and identify the NE for each of the final<br />
subgames.<br />
(2) Select one NE in each of the final subgames and replace the subgame by<br />
the payoffs that result when this NE is played.<br />
(3) Repeat steps (1) and (2) for the reduced game and continue this<br />
procedure until every move in the game is determined. This collection of<br />
moves at all information sets constitutes a profile of SPNE strategies.<br />
If at no step of this procedure multiple equilibria are encountered the SPNE is<br />
unique. If the game has perfect information and no player has the same<br />
payoffs at any two terminal nodes this is indeed the case, which proves part<br />
(b).<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 79 / 168
Remarks:<br />
1. If there are multiple equilibria in a subgame then the set of all subgame<br />
equilibria can be found by using the procedure of generalized backwards<br />
induction with every possible combination of equilibria.<br />
2. Part (b) of the proposition can be strengthened. If no player has the same<br />
payoffs at any two terminal nodes of a finite game of perfect information,<br />
then this game has a unique NE. This is Zermelo’s (1913) Theorem.<br />
<strong>3.</strong> Chess is a finite game with perfect information. Moreover, chess is a<br />
zero-sum game. It can be shown that all Nash equilibria of a zero-sum<br />
game yield the same equilibrium payoffs for all players. Thus, it must be<br />
the case that in all Nash equilibria of chess either white wins or black<br />
wins or there is a remi. Furthermore, the solution to the game can be<br />
found by backward induction. Thus, from a game theoretic perspective<br />
chess is trivial.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 80 / 168
Example: A <strong>Game</strong> with Imperfect Information<br />
Consider the following game with two periods, in which two players play a<br />
prisoner’s dilemma game in period 1 and a coordination game with 0 < x < y<br />
in period 2:<br />
Period 1:<br />
B<br />
❅<br />
❅ cooperate defect<br />
A<br />
❅<br />
cooperate<br />
defect<br />
2, 2 -1, 3<br />
3, -1 0, 0<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 81 / 168
Period 2:<br />
B<br />
❅<br />
❅<br />
A<br />
❅<br />
L<br />
R<br />
ℓ r<br />
x, x 0, 0<br />
0, 0<br />
y, y<br />
FIG. <strong>3.</strong>24: SPE of a <strong>Game</strong> of Imperfect Information<br />
What are the SPNE of this game?<br />
Under which assumptions on x und y is it possible to sustain a SPNE in<br />
which both players cooperate in the first period?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 82 / 168
Subgame Perfection and Rationality<br />
Subgame perfection requires that it is common knowledge that all players are<br />
rational. This can raise difficult problems as in the following game:<br />
1<br />
.<br />
.<br />
L R<br />
ℓ<br />
2<br />
.<br />
<br />
r<br />
1<br />
L<br />
.<br />
<br />
′ R ′<br />
<br />
2<br />
0<br />
<br />
1<br />
1<br />
3<br />
0<br />
<br />
0<br />
2<br />
FIG. <strong>3.</strong>25: Rationality and Backward Induction<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 83 / 168
Backward induction implies that player 1 has to choose L and the game ends.<br />
Why?<br />
Suppose now that player 1 plays R. How should player 2 interpret this move?<br />
A rational player 1 would have chosen L.<br />
Doesn’t player 1 demonstrate that he is irrational by choosing R?<br />
But if player 1 is irrational, he may also choose R ′ at the last stage of the<br />
game.<br />
But then it would be optimal for player 2 to choose r.<br />
But if player 2 does so, a rational player 1 should anticipate this and<br />
choose R.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 84 / 168
In order to deal with this problem, Selten (1975) introduced the notion of<br />
Trembling-hand Perfect Nash Equilibrium or simply Perfect Nash<br />
Equilibrium (PNE). The idea behind this concept is as follows:<br />
1) It is common knowledge that all players are rational.<br />
2) But: All players make mistakes:<br />
◮ With probability 1 − ɛ they choose the strategy that they want to choose.<br />
◮ With probability ɛ > 0 they “tremble” and choose some other (randomly<br />
chosen) strategy.<br />
3) If a player observes that another player does not choose the equilibrium<br />
strategy he concludes that this player must have trembled.<br />
4) If trembles are uncorrelated over time, a deviation from the equilibrium<br />
strategy does not induce the other players to change their equilibrium<br />
strategies.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 85 / 168
To properly define a Perfect Nash Equilibrium for sequential games Selten<br />
introduces the notion of an “agent normal form” game. In the agent normal<br />
form of a game a player is replaced by a different agent in each information<br />
set at which he is called to move. All of his agents have exactly the same<br />
payoff function. The agent normal form makes sure that a player cannot<br />
correlate his trembles.<br />
Next, we need the notion of a perturbed game. In a perturbed game each<br />
agent of each player is constrained to choose each possible strategy with a<br />
probability of at least ɛ(si) > 0.<br />
An ɛ-constrained equilibrium is a totally mixed strategy profile σ ɛ such that,<br />
for each player i, σ ɛ i solves maxσi ui(σi, σ−i) subject to σi(si) ≥ ɛ(si) for all si<br />
und for some {ɛ(si)}si ∈Si , i∈I with 0 < ɛ(si) < ɛ.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 86 / 168
Definition <strong>3.</strong>16 ((Trembling-hand) Perfect Nash Equilibrium)<br />
A Nash equilibrium is (trembling-hand) perfect if it is any limit of<br />
ɛ-constrained equilibria σ ɛ as ɛ goes to 0.<br />
Note that any trembling hand-perfect equilibrium is subgame perfect. The<br />
reason is that each subgame is reached with strictly positive probability, and<br />
so strategies have to be best responses in all subgames.<br />
Note also that is often very difficult to verify whether a strategy profile is a<br />
trembling-hand perfect equilibrium. Therefore, we will restrict attention<br />
Subgame Perfect Nash Equilibria in the following.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 87 / 168
The One-shot Deviation Principle<br />
If a game has many stages it may become very difficult to check whether an<br />
equilibrium candidate is indeed an equilibrium. The reason is that if a player<br />
moves at several stages, then his set of possible strategies becomes very<br />
large very quickly. In principle all of these strategies have to be checked in<br />
order to see whether there is a profitable deviation. However, the following<br />
proposition tells us that this task can be simplified dramatically.<br />
Proposition <strong>3.</strong>10 (One-shot Deviation Principle)<br />
A strategy profile s ∗ is a SPNE if and only if there does not exist any player i<br />
and any strategy ˜si that differs from s ∗ i in one period t and after one history h t<br />
only and is strictly better than s ∗ i if the subgame after h t is reached.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 88 / 168
Remarks:<br />
1) Why is this condition a necessary condition for a SPNE?<br />
2) It is less obvious that this condition is also sufficient. Even if there does<br />
not exist a profitable strategy ˜si differing from s∗ i at only one information<br />
set, there could still be a profitable strategy ˜si deviating at multiple<br />
information sets from s∗ i .<br />
3) The one-shot deviation principle makes life much easier. Now we only<br />
have to check whether there is any information set at which a player has<br />
an incentive to deviate. We do not have to consider entire strategies that<br />
differ at several information sets from the proposed equilibrium strategy.<br />
4) We do the proof for finite games only. However, it also applies to games<br />
with an infinite horizon if players discount future payoffs.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 89 / 168
Proof: The proof is by contradiction. Consider a strategy profile s∗ that<br />
satisfies the one-shot deviation condition, but that is not a SPNE. Then there<br />
exists a strategy ˜si for some player i that deviates from s∗ i at at least two<br />
information sets and that yields a strictly higher payoff for player i.<br />
Consider the last information set at which there is a deviation from s∗ i . If ˜si<br />
does not yield a strict improvement for player i if this information set is<br />
reached, replace this part of ˜si by the corresponding part of s∗ i and go to the<br />
next “last” information set at which ˜si and s∗ i differ until you have found an<br />
information set at which ˜si yields a strictly higher payoff then s ∗ i if this<br />
information set is reached. Call the history that leads to this information set ˜ h ˜t .<br />
Consider now a strategy that ˆsi that coincides with s ∗ i in all information sets<br />
except for those following after ˜ h ˜t where it coincides with ˜si. However, ˜si<br />
coincides with s ∗ i in all information sets except for the one at ˜ h ˜t . Hence, ˆsi<br />
deviates from s ∗ i only at ˜ h ˜t . By the construction of ˆsi it must be the case that ˆsi<br />
yields a strictly higher payoff than s ∗ i if ˜ h ˜t is reached. This is a contradiction to<br />
our assumption that s ∗ satisfies the one-shot deviation condition. Q.E.D.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 90 / 168
Infinite <strong>Game</strong>s<br />
A War of Attrition:<br />
Consider two players who fight for a prize. In each period t, t = 1, 2, . . ., each<br />
player decides whether to fight or to give up:<br />
If both players fight, both lose one unit of utility and the game moves on<br />
to the next period.<br />
If one player gives up and the other one fights, the fighter wins and gets<br />
the prize of v > 1 while the loser gets 0 and the game ends.<br />
Payoffs: Let ˆt denote the period in which the loser gives up.<br />
Loser:<br />
Winner:<br />
uL(ˆt) = −(1 + δ + · · · + δ ˆt−1 ) · 1 = − 1 − δ ˆt<br />
1 − δ<br />
ug(ˆt) = −(1 + δ + · · · + δ ˆt−1 ) · 1 + δ ˆt v = − 1 − δ ˆt<br />
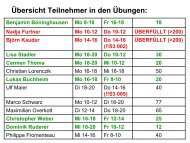
1 − δ + δˆt v<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 91 / 168
Is there a symmetric, stationary SPNE?<br />
A symmetric equilibrium must be in mixed strategies. Suppose that both<br />
players give up each period with probability p and fight with probability 1 − p.<br />
These strategies are an equilibrium if in each period both players are<br />
indifferent whether to fight or to give up. Thus, we must have in every period t:<br />
0 = p v + (1 − p) · [−1 + δ · 0]<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 92 / 168
Interpretation:<br />
All losses that have been accumulated up to period t are sunk costs that<br />
do not affect future play. Thus, we only have to consider future payoffs.<br />
If player i gives up in period t he gets 0 right away.<br />
If player i fights there are two possibilities:<br />
◮ With probability p his opponent gives up and he gets v.<br />
◮ With probability 1 − p his opponent fights in which case he loses 1 this<br />
period. In the next period he is again indifferent between fighting and giving<br />
up, so his continuation payoff is exactly 0.<br />
Note that we only have to check that no player has an incentive to deviate<br />
in any one period. By the One-shot Deviation Principle we do not have to<br />
check whether deviations in multiple periods are profitable.<br />
Solving for p yields:<br />
p ∗ = 1<br />
1 + v<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 93 / 168
Remarks:<br />
1) The higher the prize v, the smaller is the probability of giving up in every<br />
period.<br />
2) The outcome is inefficient because the players fight with positive<br />
probability. There is also a positive probability that the costs of fighting<br />
exceed the value of the prize.<br />
3) There are many other SPNE. For example: Player 1 fights in every period<br />
and player 2 gives up in every period is a SPNE. Why?<br />
4) But: If the situation is completely symmetric, a symmetric equilibrium may<br />
be more convincing.<br />
5) The war of attrition game is used by biologists to explain animal behavior<br />
(Maynard Smith 1974). Interpretation?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 94 / 168
Repeated <strong>Game</strong>s<br />
Let G denote a finite game in normal or extensive form. Then G T is a<br />
repeated game in extensive form in which the stage game G is played T<br />
times in a row, with T ∈ IN ∪ {∞}.<br />
Examples:<br />
Two players play a repeated prisoner’s dilemma game.<br />
Two oligopolists play a repeated Cournot game, etc.<br />
Remarks:<br />
1) Repeated games are a special case of dynamic games.<br />
2) But, because of their special structure they have some interesting<br />
properties that do not hold for all dynamic games.<br />
3) Be careful: The following games are not repeated games:<br />
◮ The war of attrition game<br />
◮ A bargaining game in which the players take turns in making offers<br />
◮ Investment games, resource extraction games, etc.<br />
Why not?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 95 / 168
Finitely Repeated <strong>Game</strong>s<br />
Suppose that the prisoners’ dilemma game is played by two players two times<br />
in a row:<br />
ℓ r<br />
L<br />
R<br />
1, 1 5, 0<br />
0, 5 4, 4<br />
FIG. <strong>3.</strong>26: Repeated Prisoner’s Dilemma <strong>Game</strong><br />
The payoffs of the repeated game are simply the sums of the payoffs of the<br />
two stage games.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 96 / 168
Analysis of the <strong>Game</strong><br />
Period 2: No matter what has happened in period 1, the prisoner’s dilemma<br />
game has a unique Nash Equilibrium (L, ℓ) that must be played in period 2 in<br />
every SPNE.<br />
Period 1: What happens in period 1 has no impact on what is going to<br />
happen in period 2. Therfore, we can simply add the payoffs (1,1) from period<br />
t to the payoffs in period 1.<br />
L<br />
R<br />
ℓ r<br />
2, 2 6, 1<br />
1, 6 5, 5<br />
FIG. <strong>3.</strong>27: Reduced Normal Form of the Repeated Prisoner’s Dilemma<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 97 / 168
Conclusion:<br />
Both players should choose “left” in period 1.<br />
The unique SPNE is:<br />
◮ Equilibrium strategy of player 1: (L1, L2L2L2L2)<br />
◮ Equilibrium strategy of player 2: (ℓ1, ℓ2ℓ2ℓ2ℓ2)<br />
Proposition <strong>3.</strong>11<br />
If the stage game G has a unique NE, then the finitely repeated game G T ,<br />
T < ∞, has a unique SPNE that is simply the T -fold repetition of the NE of<br />
the stage game.<br />
Proof: Follows immediately from the principles of backward induction and<br />
subgame perfection as in the repeated prisoner’s dilemma game. Q.E.D.<br />
Exercise: Show that the equilibrium described for the repeated prisoner’s<br />
dilemma is not just the unique SPNE but also the unique NE.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 98 / 168
Consider now the following stage game that is played twice in a row:<br />
2<br />
❅<br />
❅<br />
1<br />
❅<br />
L<br />
M<br />
R<br />
ℓ m r<br />
1, 1 5, 0 0, 0<br />
0, 5 4, 4 0, 0<br />
0, 0 0, 0 3, 3<br />
FIG. <strong>3.</strong>28: Multiple Nash Equilibria in the Stage <strong>Game</strong><br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 99 / 168
How many pure strategies does every player have in the repeated game?<br />
The stage game has two NE in pure strategies: (L, ℓ) and (R, r).<br />
Proposition <strong>3.</strong>12<br />
It is a SPNE to play the same NE of the stage game in every period.<br />
Proof: Subgame perfection requires that a NE is played in every subgame. In<br />
the last period this is obviously the case. Because play in the second last<br />
period does not affect what happens in the last period, we also have a NE in<br />
the subgame starting in the second to last period, and so on. Q.E.D.<br />
But: There are many additional SPNE. Example:<br />
Period 1: Both players play (M, m) in period 1.<br />
Period 2:<br />
If both players choose these actions in period 1 they play (R, r)<br />
in period 2.<br />
If at least one player deviated from (M, m), they play (L, ℓ) in<br />
period 2.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 100 / 168
Remarks:<br />
This equilibrium yields payoffs (7, 7) that are higher than the payoffs<br />
(6, 6) that the players would get if they played (R, r) twice.<br />
In this equilibrium cooperation in period 1 is sustained by the threat to<br />
play the “bad” NE (L, ℓ).<br />
This threat is subgame perfect. But is it really credible? What if players<br />
can renegotiate?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 101 / 168
Infinitely Repeated <strong>Game</strong>s<br />
In finitely repeated games the “last period effect” plays a crucial role. If there<br />
is a unique NE in the stage game, we know what we are going to do in the last<br />
period. But then we also know what we will do in the second to last period,<br />
and the game unravels. Thus, in any finite repetition of the prisoner’s dilemma<br />
game the unique SPNE is that all players always defect. This seems very<br />
implausible.<br />
Experiments have shown that it is indeed often the case that cooperation<br />
breaks down in the last period. Nevertheless, players manage to cooperate in<br />
most previous periods.<br />
Axelrod experiments.<br />
If players do not solve the game by backward induction it may be better to<br />
describe a repeated relationship as an infinitely repeated game, even if there<br />
are no infinitely repeated games in the real world.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 102 / 168
Payoffs<br />
If a player would maximize the sum of his payoffs in an infinitely repeated<br />
game his utility would always be infinite and his maximization problem would<br />
not be well defined.<br />
We assume that players have a discount factor δ < 1 and maximize the<br />
discounted sum of future payoffs. Possible Interpretations:<br />
δ = 1<br />
1+r , where r > 0 is the interest rate,<br />
δ is the probability that there is a next period,<br />
or δ reflects a combination of the two.<br />
Furthermore, we normalize all payoffs in the repeated game by multiplying<br />
them with (1 − δ) in order to make them comparable to the payoffs of the<br />
one-shot game. Why can we do this without loss of generality?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 103 / 168
Definition <strong>3.</strong>17<br />
An infinitely repeated stage game G with discount factor δ is denoted by<br />
G ∞ (δ). The payoff of player i in G ∞ (δ) is given by<br />
vi = (1 − δ)<br />
∞<br />
δ t−1 ui(a t i , at −i ).<br />
t=1<br />
Example: If player i gets payoff 4 in every period, his payoff in the repeated<br />
game is<br />
∞<br />
vi = (1 − δ) δ t−1 4 = (1 − δ) 1<br />
4 = 4.<br />
1 − δ<br />
t=1<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 104 / 168
Proposition <strong>3.</strong>13<br />
If δ is sufficiently close to 1, there exists a SPNE in the infinitely repeated<br />
prisoner’s dilemma game in which both players cooperate in all periods on the<br />
equilibrium path.<br />
Proof: Consider the following symmetric pair of strategies for players i and j:<br />
“Play ‘cooperate’ in period 1 and in all following periods as long as<br />
both players played ‘cooperate’ in all previous periods. However, if at<br />
least one player deviated in any previous period, then choose ‘defect’<br />
forever after.<br />
Consider the payoffs in Fig. <strong>3.</strong>26:<br />
If both players follow their equilibrium stragegies, each of them gets<br />
(1 − δ)<br />
∞<br />
t=1<br />
δ t−1 4 = (1 − δ) 1<br />
4 = 4 .<br />
1 − δ<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 105 / 168
If one player deviates in this period, his payoff is<br />
<br />
∞<br />
(1 − δ) 5 + δ t−1 <br />
1 = (1 − δ) 5 + δ<br />
<br />
= 5 − 4δ .<br />
1 − δ<br />
t=2<br />
A deviation is profitable if and only if 4 < 5 − 4δ ⇔ δ < 1<br />
4 .<br />
Thus, for δ ≥ 1<br />
4 the above strategies form a NE.<br />
We still have to show that these strategies are also a SPNE.<br />
We have shown already that a deviation after a history, in which all<br />
players always cooperated is not profitable if δ ≥ 1<br />
4 .<br />
Suppose now that we are off the equilibrium path, i.e. at least one player<br />
has deviated at least once in the past. In this case a deviation does not<br />
pay either. Both players are supposed to defect forever after. But this is<br />
just the repetition of the one-shot NE, which is always subgame perfect.<br />
Q.E.D.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 106 / 168
Remarks:<br />
These strategies are called “grim strategies” or “trigger strategies”. They<br />
have the drawback that a mistake of one the players triggers a<br />
catastrophe for everybody (“doomsday machine”).<br />
It is possible to sustain cooperation with other punishment strategies, e.g.<br />
with “perfect tit-for-tat”:<br />
“Play ‘cooperate’ in period 1 and whenever the outcome of the<br />
last period was either (‘cooperate’, ‘cooperate’) or (‘defect’,<br />
‘defect’). Play ‘defect’ if the outcome of the last period was<br />
(‘cooperate’, ‘defect’) or (‘defect’, ‘cooperate’)”<br />
Exercise 1: Show that it is a SPNE if both players play “perfect tit-for-tat”<br />
if δ is sufficiently close to 1. Use the one-shot-deviation principle. You<br />
have to check four cases.<br />
Exercise 2: Show that it is not a SPNE if both players play “tit-for-tat”<br />
(“Cooperate in period 1. In all following periods play the strategy used by<br />
your opponent in the previous period.”)<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 107 / 168
The proposition shows that the efficient outcome can be implemented<br />
(i.e. is a SPNE outcome) if players play an infinitely repeated game and if<br />
the discount factor is sufficiently close to one. However, there are many<br />
other SPNE outcomes. The “Folk-Theorem” shows that any payoff vector<br />
that gives each player at least his minmax payoff can be sustained as a<br />
SPNE outcome.<br />
Discussion.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 108 / 168
<strong>3.</strong>3 Static <strong>Game</strong>s with Incomplete Information<br />
So far we assumed that there is common knowledge about the game itself,<br />
i.e.<br />
all players know the set of players,<br />
all players know what the strategy sets of all players are,<br />
all players know what the payoff functions of all players are,<br />
and everybody knows that everybody knows that ...<br />
How can we model games with incomplete information, e.g. games<br />
in which a player does not know which actions are feasible for his<br />
opponent,<br />
or what the payoff function of his opponent is,<br />
or what information his opponent has when he is called to move?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 109 / 168
Harsanyi (1967/68) suggested how to transform a game with incomplete<br />
information into a game with imperfect information that we know how to deal<br />
with.<br />
He suggested that all private information of a player is summarized in his<br />
“type”. Thus, for each player i with private information we have to specify his<br />
type space Ti, i.e. what possible types ti ∈ Ti he may have.<br />
The utility function of a player may now depend on his type, i.e.<br />
ui = ui(ai, a−i, ti) ,<br />
or, slightly more formally: ui : Ai × A−i × Ti → R.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 110 / 168
Examples:<br />
Player i has private information about his payoffs, e.g. about his cost to<br />
do something, his willingness to pay for something, etc.<br />
Player i has private information about his strategy set. Let Ai denote the<br />
set of all actions that are feasible. If player i cannot use some action<br />
âi ∈ Ai, then he is of a type ˆti ∈ Ti for whom the cost of taking action âi is<br />
infinitely high, i.e.<br />
ui(âi, a−i,ˆti) = −∞ .<br />
Thus, action ai is strictly dominated and will never be taken.<br />
Player i may be an “irrational” player who always chooses some action āi<br />
no matter what the payoff consequences are. Then the player is of type<br />
¯ti ∈ Ti with utility function<br />
<br />
1 if ai = āi<br />
ui(ai, a−i,¯ti) =<br />
0 if ai = āi<br />
For this type it is a dominant strategy to play āi.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 111 / 168
The structure of the game is now as follows:<br />
At stage 0 nature draws the types of all players according to some joint<br />
cumulative distribution function F(t), t ∈ T , with t = (t1, t2, . . . , tI) and<br />
T = T1 × T2 × . . . × TI.<br />
F(t) is common knowledge among all players.<br />
Note that the types of different players may be correlated.<br />
Each player learns his own type and updates his beliefs about the<br />
probabilities of the types of the other players. The updated cumulative<br />
distribution function of player i of type ti over the possible types t−i of his<br />
opponents is denoted by F (t−i|ti).<br />
Then the game is played.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 112 / 168
Beliefs<br />
The cumulative distribution function F(t−i|ti) is called the “belief” of<br />
player i.<br />
The assumption that all players start out with the same prior probability<br />
distribution (the same “prior”) F (t) is very important. Players may have<br />
very different information assigned to them by nature, but they all agree<br />
which events are possible and which are not. It also implies that it is<br />
common knowledge that the beliefs of player i with type ti are pi(t−i | ti).<br />
If the types of the players are correlated, a player learns something about<br />
the probabilities of the types of his opponent when he learns his own<br />
type. In this case each player has to use Bayes’ rule to update his beliefs:<br />
prob(A | B) =<br />
Example: Auction for drilling rights.<br />
prob(A ∩ B)<br />
prob(B)<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 113 / 168
If the types of the players are stochastically independent we have<br />
pi(t−i|ti) = p(t−i) · p(ti)<br />
p(ti)<br />
= p(t−i) ∀ti ∈ Ti<br />
where pi(t−i | ti) is the probability player i of type ti assigns to the type<br />
profiles t−i of his opponents. In this case a player’s beliefs are<br />
independent of his own type.<br />
Because of the importance of Bayes’ Rule games with incomplete<br />
information are called Bayesian <strong>Game</strong>s.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 114 / 168
Strategies<br />
Different types of player i may choose different actions. Therefore, we have to<br />
refine the notion of a strategy.<br />
Definition <strong>3.</strong>18 (Strategies in <strong>Game</strong>s with Incomplete<br />
Information)<br />
A pure strategy of player i assigns to each possible type of player i an action<br />
ai, i.e. si : Ti → Ai.<br />
A mixed strategy of player i assigns to each possible type of player i a<br />
probability distribution over Ai, i.e. σi : Ti → ∆(Ai).<br />
Note that each player has to specify a strategy not just for his realized type but<br />
also for all other potential types that he could have had. Why?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 115 / 168
Expected Payoffs<br />
Suppose that player i is of type ti and expects his opponents to play the<br />
strategy profile<br />
s−i(t−i) = (s1(t1), . . . , si−1(ti−1), si+1(ti+1), . . . , sN(tN))<br />
His updated beliefs about the types of his opponents are p(t−i|ti).<br />
If player i with type ti chooses action ai, he gets with probability p(t−i|ti) the<br />
payoff<br />
ui(ai, s−i(t−i), ti).<br />
Thus, his expected payoff is given by<br />
E[ui(ai, s−i, ti)] = <br />
t−i ∈T−i<br />
pi(t−i|ti) ui(ai, s−i(t−i), ti).<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 116 / 168
Definition <strong>3.</strong>19 (Normal Form of a Bayesian <strong>Game</strong>)<br />
The normal form of a game G = [I; {Si}; {Ti}; F (·); {ui}] consists of<br />
(1) the set of players, I = {1, . . . , n},<br />
(2) the strategy sets of all players {Si} = {S1, . . . , Sn},<br />
(3) the type spaces T1, . . . , Tn of the players,<br />
(4) the common prior F(t)<br />
(5) the payoff functions of all players {ui} = {u1, . . . , un}.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 117 / 168
Bayesian Nash Equilibrium<br />
Definition <strong>3.</strong>20<br />
A strategy profile s ∗ = (s ∗ 1 , . . . , s∗ n) is a Bayesian Nash Equilibrium of a<br />
game with incomplete information, if for all i = 1, . . . , n and all ti ∈ Ti the<br />
action ai = s ∗ i (ti) maximizes E ui(ai, s ∗ −i , ti) .<br />
Remarks:<br />
1) The idea of a Bayesian Nash Equilibrium is exactly the same as the idea<br />
of a NE. Each player must play a best response given the strategies<br />
played by his opponents. But now this condition has to hold for all<br />
possible types of each player.<br />
2) The beliefs of each player about the types of his opponents have to be<br />
formed using Bayes’ rule.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 118 / 168
3) If players choose mixed strategies they take the expectation over all<br />
possible actions that are chosen with positive probability by each possible<br />
type:<br />
Let σk(ak|tk) denote the probability with which player k of type tk chooses<br />
action ak. Thus, if the type profile is t−i, a−i is played with probability<br />
σ−i(a−i|t−i) = <br />
k=i σk(ak|tk).<br />
Player i’s expected payoff if he is of type ti and chooses ai is therefore<br />
E[ui(ai, σ−i, ti)] = <br />
t−i ∈T−i<br />
pi(t−i|ti) <br />
a−i ∈A−i<br />
σ−i(a−i|t−i) ui(ai, a−i, ti).<br />
4) σi is a best response to σ−i if for all ti ∈ Ti each action ai with σi(ai|ti) > 0<br />
maximizes E[ui(ai, σ−i, ti)].<br />
5) In finite games with incomplete information there always exists a<br />
Bayesian Nash Equilibrium, possibly in mixed strategies. The proof<br />
follows the same lines as the existence proof for NE.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 119 / 168
Purification of Mixed Strategies<br />
In Chapter <strong>3.</strong>1 we offered one justification for mixed strategy equilibria that<br />
goes back to Harsanyi. Harsanyi argued that a mixed strategy equilibrium can<br />
be interpreted as the limit of a sequence of pure strategy equilibria of a<br />
perturbed game with incomplete information as the perturbation goes to zero.<br />
To illustrate this argument consider again the “battle of the sexes” game.<br />
However, we now assume that each player is imperfectly informed about the<br />
payoff function of his opponent:<br />
Player 2 does not know exactly what player 1’s payoff is if they both go to<br />
“Boxing”. She believes that his payoff is 2 + t1 in this case, where t1<br />
uniformly distributed on the interval [0, x].<br />
Player 1 does not know exactly what player 2’s payoff is if they both go to<br />
“Ballet”. He believes that her payoff is 2 + t2 in this case, where t2 is<br />
uniformly distributed on the interval [0, x].<br />
Note that the types of two players are uncorrelated. Thus, by learning his or<br />
her own type no player learns anything about the type of his or her opponent.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 120 / 168
2<br />
❅<br />
❅ Boxing Ballet<br />
1<br />
❅<br />
Boxing<br />
Ballet<br />
2 + t1, 1 0, 0<br />
0, 0 1, 2 + t2<br />
FIG. <strong>3.</strong>29: Battle of the Sexes with Incomplete Information<br />
We are going to construct a Bayesian Nash Equilibrium in pure strategies in<br />
which<br />
player 1 chooses “Boxing” iff t1 ≥ c1;<br />
player 2 chooses “Ballet” iff t2 ≥ c2.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 121 / 168
In this equilibrium<br />
the probability assigned by player 2 to the event that player 1 chooses<br />
“Boxing” is equal to x−c1<br />
x ;<br />
the probability that player 1 assigns to the event that player 2 goes to<br />
“Ballet” is equal to x−c2<br />
x .<br />
For which values of c1 and c2 do these strategies form a Bayesian Nash<br />
Equilibrium?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 122 / 168
Player 1 prefers “Boxing” iff:<br />
(1 −<br />
Player 2 prefers “Ballet” iff:<br />
(1 −<br />
E(u1|Bo) ≥ E(u1|Ba)<br />
x − c2<br />
) · (2 + t1) ≥<br />
x<br />
t1 ≥ x<br />
x − c2<br />
x<br />
c2<br />
· 1<br />
− 3 ≡ c1<br />
E(u2|Ba) ≥ E(u2|Bo)<br />
x − c1<br />
) · (2 + t2) ≥<br />
x<br />
t2 ≥ x<br />
x − c1<br />
x<br />
c1<br />
· 1<br />
− 3 ≡ c2<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 123 / 168
This implies for c1 and c2:<br />
Solving for c:<br />
c1 = c2 = c and c 2 + 3c − x = 0<br />
c = − 3<br />
2 +<br />
<br />
9 + 4x<br />
4<br />
Hence, the probability with which player 1 chooses “Boxing” (player 2 chooses<br />
“Ballet”) is:<br />
√<br />
x − c 9 + 4x − 3<br />
= 1 −<br />
x 2x<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 124 / 168
What happens if the incomplete information becomes small, i.e. if x → 0?<br />
lim<br />
x→0<br />
√ 9 + 4x − 3<br />
2x<br />
(<br />
= lim<br />
x→0<br />
√ 9 + 4x − 3)( √ 9 + 4x + 3)<br />
2x( √ 9 + 4x + 3)<br />
= lim<br />
x→0<br />
9 + 4x − 9<br />
2x( √ 9 + 4x + 3)<br />
2<br />
= lim √ =<br />
x→0 9 + 4x + 3 1<br />
3<br />
Conclusion: The mixed strategy equilibrium <br />
2 1<br />
3 , 3 of the “battle of the sexes”<br />
game with complete information can be interpreted as the mixed Bayesian<br />
Nash Equilibrium of a perturbed game with incomplete information when the<br />
perturbation goes to zero.<br />
Harsanyi (1973) has shown that this “purification” of mixed strategy equilibria<br />
works out in almost all games.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 125 / 168
<strong>3.</strong>4 Dynamic <strong>Game</strong>s with Incomplete Information<br />
In dynamic games with incomplete information we want to refine the Bayesian<br />
Nash Equilibrium concept in order to rule out equilibria that are not credible.<br />
Problem: Subgame perfection has no bite in these games.<br />
If a player does not know the type of his opponent, there are no proper<br />
subgames starting from a singleton information set after nature has drawn the<br />
types of the players. The only subgame is the entire game!<br />
How to generalize the idea of sequential rationality to games with incomplete<br />
information?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 126 / 168
Generalization of the idea of subgame perfection to “continuation<br />
games”<br />
A “continuation game” may start at any information set<br />
But: a player must have “beliefs” about where he is in this information set,<br />
i.e. he must have a probability distribution over all possible decision<br />
nodes in this information set.<br />
Furthermore: These beliefs must be “consistent”.<br />
This generalization is useful not only in games of incomplete but also in<br />
games of complete information.<br />
It will lead us to the notion of Perfect Bayesian Equilibrium.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 127 / 168
Continuation <strong>Game</strong>s<br />
Consider the following game that is due to Selten (1975):<br />
1<br />
. .. . <br />
ℓ<br />
✎<br />
.<br />
.<br />
✍<br />
L<br />
r<br />
2<br />
M<br />
ℓ<br />
☞<br />
. .<br />
✌<br />
r<br />
2<br />
1<br />
0<br />
0<br />
0<br />
2<br />
What should player 2 do in this game?<br />
R<br />
<br />
0<br />
1<br />
FIG. <strong>3.</strong>30: Selten’s Horse<br />
<br />
1<br />
3<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 128 / 168
If player 2 is called to move, it is a dominant strategy to play ℓ.<br />
Anticipating this, player 1 should play L.<br />
Does this game have other equilibria?<br />
2<br />
❅<br />
❅<br />
1<br />
❅<br />
L<br />
M<br />
R<br />
ℓ r<br />
2, 1 0, 0<br />
0, 2 0, 1<br />
1, 3 1, 3<br />
FIG. <strong>3.</strong>31: Normal Form of Selten’s Horse<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 129 / 168
(R, r) is also a Nash Equilibrium of this game!<br />
Is this equilibrium subgame perfect?<br />
To impose sequential rationality we need the following definition:<br />
Definition <strong>3.</strong>21 (Continuation <strong>Game</strong>)<br />
A continuation game is a subset of an extensive form game with the<br />
following properties:<br />
a) It begins at any information set, contains all the decision nodes that are<br />
successors (both immediate and later) of this node, and contains only<br />
these nodes.<br />
b) In every information set the player who is called to move must have a<br />
belief that specifies the probability he assigns to the event that he is at<br />
any decision node of this information set.<br />
Given the definition of continuation games we can now define “sequential<br />
rationality” as follows:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 130 / 168
Definition <strong>3.</strong>22 (Sequential Rationality)<br />
A player must choose a strategy that is a best response to the strategies of<br />
his opponents given his beliefs in any continuation game of the game.<br />
Applying this definition to Selten’s Horse, we see that playing r is not an<br />
optimal response for player 2 no matter what he believes at which decision<br />
node he is: For any probability µ, 0 ≤ µ ≤ 1, that he is at the left decision<br />
node his optimal strategy is ℓ.<br />
This example is very simple because player 2 has a dominant strategy in the<br />
information set where he is called to move. If he does not have a dominant<br />
strategy, his optimal strategy depends in general on his beliefs.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 131 / 168
Consider the following modification of Selten’s Horse:<br />
1<br />
. .. . <br />
✎<br />
✍<br />
ℓ<br />
[µ] .<br />
.<br />
L<br />
r<br />
2<br />
M<br />
ℓ<br />
. . [1 − µ]<br />
r<br />
2<br />
1<br />
0<br />
0<br />
0<br />
0<br />
R<br />
<br />
0<br />
1<br />
<br />
1<br />
3<br />
☞<br />
✌<br />
FIG. <strong>3.</strong>32: No Dominant Strategy for Player 2<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 132 / 168
In this game, player 2 should choose ℓ only if µ ≥ 0.5. There are two<br />
sequentially rational equilibria of this game:<br />
(L, ℓ, µ ≥ 0.5)<br />
(R, r, µ ≤ 0.5)<br />
So far, we did not ask where the beliefs come from.<br />
Consider the first equilibrium (L, ℓ, µ ≥ 0.5):<br />
Given that player 2 chooses ℓ it is optimal for player 1 to choose L.<br />
Given the belief µ ≥ 0.5 it is optimal for player 2 to choose ℓ.<br />
Are all beliefs µ ≥ 0.5 consistent with player 1’s strategy to choose L with<br />
probability 1. No. If player 2 uses Bayes’ rule to derive the probability of<br />
being in the left decision node, he should conclude that µ = 1.<br />
Therefore, the only equilibrium with consistent beliefs is (L, ℓ, µ = 1).<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 133 / 168
What about the equilibrium (R, r, µ ≤ 0.5)?<br />
Given that player 2 chooses r it is optimal for player 1 to choose R.<br />
Given the belief µ ≤ 0.5 it is optimal for player 2 to choose r.<br />
Now Bayes’ Rule cannot be applied. Given that player 1 chooses R it is a<br />
zero probability event that player 2 is called to move. Thus, any belief µ is<br />
consistent with player 1’s strategy.<br />
Therefore, for any µ ≤ 0.5 the equilibrium (R, r, µ ≤ 0.5) is consistent.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 134 / 168
This discussion motivates the following definition:<br />
Definition <strong>3.</strong>23 (Perfect Bayesian Equlibrium)<br />
A (weak) Perfect Bayesian Equilibrium is a profile of strategies σ ∗ and a<br />
system of beliefs µ ∗ such that<br />
the strategies σ ∗ of all players are sequentially rational given the system<br />
of beliefs µ ∗<br />
the system of beliefs µ ∗ is consistent with the strategies s ∗ , i.e. they are<br />
derived from the equilibrium strategies using Bayes’ Rule whenever it<br />
applies.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 135 / 168
Remarks:<br />
1. If players use mixed strategies that assign positive probabilities to all<br />
possible actions in all information sets, then all decision nodes will be<br />
reached with positive probability. In this case Bayes’ rule can always be<br />
used to update beliefs and it pins down beliefs uniquely.<br />
2. If a strategy chooses an action with probability zero then it is possible that<br />
some information sets are reached with probability zero. In these<br />
information sets Bayes’ rule cannot be applied. So far we allow for<br />
arbitrary beliefs in these information sets.<br />
<strong>3.</strong> The same equilibrium outcome may be supported by different out off<br />
equilibrium beliefs. Thus, (R, r, µ ≤ 0.5) is not one Perfect Bayesian<br />
Equilibrium but a continuum of Perfect Bayesian Equilibria.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 136 / 168
Applying Bayes’ Rule:<br />
Consider again Selten’s game with the payoffs left unspecified and suppose<br />
that player 1 chooses the mixed strategy (p, q, 1 − p − q).<br />
. .. . <br />
[µ] <br />
. [1 − µ]<br />
.<br />
1 (1 − p − q)<br />
p q R<br />
✎<br />
✍<br />
ℓ<br />
L<br />
.<br />
r<br />
2<br />
ℓ<br />
M ☞<br />
✌<br />
r<br />
FIG. <strong>3.</strong>33: A Fully Mixed Strategy of Player 1<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 137 / 168
Suppose that player 2 is called to move. What is the probability that he is at<br />
the left decision node?<br />
There are three possible events: L, M and R.<br />
When player 2 is called to move, he knows that either L or M has happened.<br />
Define the following events:<br />
A = {L}<br />
B = {L, M}<br />
Now we can derive the following probabilities:<br />
prob(A ∩ B) = p<br />
prob(B) = p + q<br />
prob(A | B) = prob(A∩B)<br />
prob(B)<br />
= p<br />
p+q<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 138 / 168
Examples:<br />
1<br />
.<br />
D<br />
...<br />
2 .<br />
.<br />
✎<br />
✍<br />
ℓ<br />
[µ] .<br />
<br />
L<br />
r<br />
3<br />
R<br />
ℓ<br />
. . [1 − µ]<br />
r<br />
⎛<br />
⎝ 1<br />
2<br />
1<br />
⎞<br />
⎠<br />
⎛<br />
⎝ 3<br />
3<br />
3<br />
⎞<br />
⎠<br />
⎛<br />
⎝ 0<br />
1<br />
2<br />
⎞<br />
⎠<br />
A<br />
⎛<br />
⎝ 0<br />
1<br />
1<br />
⎛<br />
⎝ 2<br />
0<br />
0<br />
⎞<br />
⎠<br />
☞<br />
✌<br />
FIG. <strong>3.</strong>34: Example <strong>3.</strong>1: A PBE that is not a SPNE<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 139 / 168<br />
⎞<br />
⎠
Analysis of Example <strong>3.</strong>1:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 140 / 168
1<br />
. <br />
...<br />
2 .<br />
.. <br />
A<br />
A<br />
.<br />
.<br />
L<br />
3<br />
R<br />
. .<br />
′<br />
D<br />
⎛<br />
⎝<br />
ℓ r ℓ r<br />
2<br />
0<br />
0<br />
⎛<br />
⎝<br />
⎞<br />
⎠<br />
0<br />
2<br />
⎞<br />
⎠<br />
✎<br />
✍<br />
[µ] [1 − µ]<br />
0<br />
☞<br />
✌<br />
⎛<br />
⎝ 1<br />
2<br />
1<br />
⎞<br />
⎠<br />
⎛<br />
⎝ 3<br />
3<br />
3<br />
⎞<br />
⎠<br />
⎛<br />
⎝ 0<br />
1<br />
2<br />
⎞<br />
⎠<br />
⎛<br />
⎝ 0<br />
1<br />
1<br />
FIG. <strong>3.</strong>35: Example <strong>3.</strong>2: Bayes’ Rule Cannot Be Applied<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 141 / 168<br />
⎞<br />
⎠
Analysis of Example <strong>3.</strong>2:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 142 / 168
1 .<br />
.. <br />
✎<br />
✍<br />
[µ] .<br />
.<br />
L<br />
2<br />
M<br />
. . [1 − µ]<br />
ℓ r ℓ r<br />
1<br />
1<br />
5<br />
0<br />
3<br />
1<br />
R<br />
<br />
4<br />
3<br />
<br />
0<br />
2<br />
☞<br />
✌<br />
FIG. <strong>3.</strong>36: Example <strong>3.</strong>3: A Mixed Strategy PBE<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 143 / 168
Analysis of Example <strong>3.</strong>3:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 144 / 168
Restricting Out-off Equilibrium Beliefs<br />
Our definition of a (weak) Perfect Bayesian Equilibrium is the definition that is<br />
used in most of the applied literature. However, it is still very weak, because it<br />
imposes no constraints whatsoever on beliefs that are formed out of<br />
equilibrium.<br />
To see that this may be too weak consider the following two examples:<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 145 / 168
Nature<br />
.<br />
<br />
1<br />
1<br />
2<br />
✎<br />
[0.5] . .<br />
✍<br />
Player 1<br />
2<br />
☞<br />
. . [0.5]<br />
✌<br />
X Y<br />
✎<br />
[0.9] . .<br />
✍<br />
Player 2<br />
Y<br />
☞<br />
. . [0.1]<br />
✌<br />
X<br />
L R L R<br />
<br />
2<br />
10<br />
0<br />
5<br />
5<br />
2<br />
<br />
0<br />
<br />
5<br />
5 10<br />
<br />
2<br />
10<br />
FIG. <strong>3.</strong>37: Example <strong>3.</strong>4: Signal What You Don’t Know<br />
PBE: (X, L, µ1 = 0.5, µ2 = 0.9).<br />
What is fishy here?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 146 / 168
0<br />
2<br />
E<br />
.<br />
.<br />
Out In<br />
. .<br />
E<br />
✎<br />
[1.0]<br />
✍<br />
F<br />
. . M<br />
A<br />
☞<br />
. . [0.0]<br />
✌<br />
f a f a<br />
<br />
−3<br />
<br />
1<br />
−1 −2<br />
−2<br />
−1<br />
<br />
3<br />
1<br />
FIG. <strong>3.</strong>38: Example 5: A Weak PBE That Is Not Subgame Perfect<br />
PBE: ((Out, A), f , µ = 1.0).<br />
Why is this a PBE even though it is not subgame perfect?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 147 / 168
Sequential Equilibria<br />
Kreps and Wilson (1982) were the first to come up with the idea to explicitly<br />
specify the beliefs of the players at every information set of the game. They<br />
introduced the notion of Sequential Equilibrium.<br />
Definition <strong>3.</strong>24 (Sequential Equilibrium)<br />
A strategy profile σ ∗ and a system of beliefs µ ∗ form a Sequential Equilibrium<br />
if they have the following properties:<br />
(i) The strategy profiles σ∗ is sequentially rational given the belief system µ ∗ .<br />
(ii) k ∞<br />
There exists a sequence of completely mixed strategies {σ k=1} with<br />
limk→∞ σk = σ, such that µ = limk→∞ µ k , where µ k denotes the beliefs<br />
derived from strategy profile σk using Bayes’ rule.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 148 / 168
Remarks:<br />
1. All Sequential Equilibria are Perfect Bayesian Equilibria, but not all PBE<br />
are SE.<br />
2. Sequential Equilibria rule out certain out of equilibrium beliefs:<br />
◮ In Example 4 Sequential Equilibrium requires that µ = 0.5. Why?<br />
◮ In Example 5 Sequential Equilibrium requires that µ = 0.0 and M chooses a.<br />
Why?<br />
◮ In games with more than two players Sequential Equilibrium requires that all<br />
players update their beliefs off the equilibrium path in the same way. Why?<br />
<strong>3.</strong> Even though these are very desirable properties, it is very difficult to<br />
show that an equilibrium candidate is a Sequential Equilibrium in<br />
practice. This is why most applied papers construct Perfect Bayesian<br />
Equilibria, call them “Sequential Equilibria”, but do not check whether<br />
they do indeed satisfy condition (ii).<br />
4. Kreps and Wilson (1982) have shown that Sequential Equilibria exist<br />
under rather weak conditions.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 149 / 168
5. Sequential Equilibrium is closely related to (Trembling Hand) Perfect<br />
Equilibrium, but slightly weaker: Every Perfect Equilibrium is a Sequential<br />
Equilibrium but not the other way round. (Trembling Hand) Perfect<br />
Equlibria require that trembles are uncorrelated and that we find a<br />
sequence of ɛ− constrained equilibria, while Kreps and Wilson allow for<br />
correlated trembles and require only a sequence of ɛ−constrained<br />
strategies.<br />
6. For many games the set of Sequential Equilibria and the set of Perfect<br />
Equilibria coincide. See Kreps and Wilson (1982) and Fudenberg and<br />
Tirole (1991) for a discussion.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 150 / 168
Signaling <strong>Game</strong>s<br />
An important class of games with incomplete information are signaling<br />
games:<br />
Two players: a sender and a receiver<br />
Nature chooses the type of the sender out of T = {t1, . . . , tI} according to<br />
the probability distribution µ(t).<br />
The sender learns his type and chooses a message<br />
m ∈ M = {m1, . . . , mJ}.<br />
The receiver observes the message (but not the type) of the sender and<br />
chooses an action a ∈ A = {a1, . . . , aK }.<br />
Payoffs U S (t, m, a) and U R (t, m, a) are realized.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 151 / 168
Examples of Signaling <strong>Game</strong>s:<br />
Job market signaling<br />
Initial public offering<br />
Limit pricing<br />
...<br />
We start out with an abstract signaling game with two types, two messages<br />
and two actions.<br />
This material is covered by MGW, Chapter 13C, 450-460.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 152 / 168
a 1<br />
a 2<br />
a 1<br />
a 2<br />
✎☞<br />
m1 . .. . <br />
S<br />
t1 <br />
m2 a1 ✎☞<br />
. <br />
R Nature R<br />
.<br />
.. . <br />
✍✌<br />
...... . <br />
. <br />
✍✌<br />
m 1<br />
t 2<br />
S<br />
µ 0<br />
1 − µ 0<br />
FIG. <strong>3.</strong>39: Structure of a 2 × 2 × 2 Signaling <strong>Game</strong><br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 153 / 168<br />
m 2<br />
a 2<br />
a 1<br />
a 2
In this game each player has four possible strategies. [Recall: A strategy<br />
specifies for every information set what the player who is called to move in this<br />
information set is going to do.]<br />
A possible strategy of the sender is (m2, m1), i.e. “Choose m2 if your type<br />
is t1 and choose m1 if your type is t2.”<br />
A possible strategy of the receiver is (a2, a1), i.e. “Choose a2 íf the<br />
sender has chosen m1 and choose a1 if the sender has chosen m2.”<br />
Furthermore, the receiver has to specify his beliefs about the type of the<br />
sender after receiving the senders message. Because there are two different<br />
information sets for the receiver, he must have two beliefs (µ1, µ2), where µi is<br />
the probability the receiver attaches to the event that the sender is of type t1 if<br />
he observes message mi.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 154 / 168
There are two types of pure strategy equilibria:<br />
Separating equilibria: Different types of the sender choose different<br />
messages. Thus, the receiver perfectly learns the type of the sender from<br />
observing his message.<br />
Pooling equilibria: All types of the sender choose the same message.<br />
Thus, the receiver learns nothing about the type of the sender from<br />
observing his message.<br />
If there are more than two types we can also have partially separating<br />
equilibria: Some messages are used by some types and not by others, but<br />
some messages are used by different types. Thus, there is some separation<br />
but it is not perfect.<br />
With mixed strategies there may also be hybrid equilibria: One type sends<br />
one message with probability one, the other type randomizes between the two<br />
messages.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 155 / 168
Example:<br />
<br />
1<br />
3<br />
<br />
4<br />
0<br />
<br />
2<br />
4<br />
<br />
0<br />
1<br />
✎☞<br />
u<br />
µ l<br />
. .. . <br />
ℓ<br />
S<br />
t1 <br />
r<br />
✎☞<br />
u<br />
µr<br />
. <br />
d<br />
u<br />
R Nature<br />
........<br />
1<br />
2<br />
R<br />
u<br />
.<br />
.. . . <br />
. <br />
1 − µ l<br />
d<br />
✍✌<br />
ℓ t2 S<br />
r 1 − µr<br />
d<br />
✍✌<br />
FIG. <strong>3.</strong>40: Example of a Signaling <strong>Game</strong><br />
1<br />
2<br />
d<br />
<br />
2<br />
1<br />
<br />
0<br />
0<br />
<br />
1<br />
0<br />
<br />
1<br />
2<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 156 / 168
Let us go through the four possible pure strategy equilibrium candidates:<br />
1. Pooling on ℓ: If S chooses ℓ, R does not learn anything, so µl = 0.5.<br />
Thus, R will choose u.<br />
Is it indeed optimal for both types of S to choose ℓ? It is clearly optimal for<br />
type t2 who always gets 1 if he chooses r. For type t1 it is also optimal if R<br />
chooses d after observing r. This is optimal for the receiver if µr ≤ 2<br />
3 .<br />
Note that we cannot use Bayes’ rule after observing r to update beliefs.<br />
Thus, the following strategies and beliefs form a PBE:<br />
(ℓ, ℓ)(u, d), µl = 0.5, µr ≤ 2<br />
<br />
3 .<br />
2. Pooling on r: Cannot be a PBE. Why not?<br />
<strong>3.</strong> Separating (ℓ, r): Cannot be a PBE. Why not?<br />
4. Separating (r, ℓ): Can be sustained as a PBE. How?<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 157 / 168
Multiple Equilibria and Equilibrium Refinements<br />
Signaling games have many equilibria. Thus, it is difficult to predict the<br />
outcome of these games.<br />
The problem of multiple equilibria is mainly due to the lack of restrictions on<br />
out of equilibrium beliefs. Several authors have further refined the equilibrium<br />
concept in order to rule out “implausible” out of equilibrium beliefs.<br />
All these refinements ask:<br />
Is there a type who may benefit from deviating?<br />
Are there any types who can never benefit from this deviation?<br />
The latter are less likely to deviate then the former.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 158 / 168
Consider the following variation of Selten’s Horse:<br />
1<br />
. .. . <br />
✎<br />
✍<br />
ℓ<br />
[µ] .<br />
.<br />
L<br />
r<br />
2<br />
M<br />
ℓ<br />
. . [1 − µ]<br />
r<br />
3<br />
1<br />
0<br />
0<br />
1<br />
0<br />
R<br />
<br />
0<br />
1<br />
<br />
2<br />
2<br />
☞<br />
✌<br />
FIG. <strong>3.</strong>41: Example for the Dominance Argument<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 159 / 168
Analysis<br />
The analysis of the normal form shows that there are two Nash Equilibria:<br />
(L, ℓ) and (R, r).<br />
There is no proper subgame, so both equilibria a subgame perfect.<br />
What are the corresponding PBE?<br />
◮ (L, ℓ, µ = 1)<br />
◮ (R, r, µ ≤ 0.5). Note: In this equilibrium player 2’s information set is reached<br />
with probability 0 on the equilibrium path. Thus, we cannot use Bayes’ rule<br />
to update µ.<br />
Is it really plausible to assume that µ ≤ 0.5. This assumes that a<br />
deviating player 1 is more likely to choose M than to choose choose L.<br />
But M is a strictly dominated strategy! Player 1 should never choose M,<br />
and player 2 should not believe that he did so. Thus, we should have<br />
µ = 1 which destroys the second equilibrium.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 160 / 168
This motivates the following condition:<br />
Criterion <strong>3.</strong>1 (Dominance Criterion)<br />
If there are decision nodes in an information set off the equilibrium path that<br />
can be reached only if one of the players has chosen a strictly dominated<br />
strategy then these decision nodes have to be assigned probability 0,<br />
provided that there is at least one other decision node that can be reached<br />
without using a strictly dominated strategy.<br />
Remarks:<br />
1. The equilibrium (R, r, µ ≤ 0.5) does not satisfy Criterion <strong>3.</strong>1. Thus, the<br />
Dominance Criterion rules out this equilibrium.<br />
2. If the payoff for player 1 after (L, ℓ) is changed to 1.5 rather than 3, then<br />
both L and M are strictly dominated. In this case Criterion <strong>3.</strong>1 has no bite.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 161 / 168
The Dominance Criterion in a Signaling <strong>Game</strong><br />
<br />
3<br />
2<br />
<br />
2<br />
0<br />
<br />
1<br />
0<br />
<br />
1<br />
1<br />
✎☞<br />
✎☞<br />
u<br />
[µ l ]<br />
. .. . <br />
L<br />
S<br />
t2 <br />
R<br />
[µr ]<br />
. <br />
u<br />
d<br />
R Nature R<br />
u<br />
........<br />
1<br />
2<br />
u<br />
.<br />
.. . . <br />
. <br />
[1 − µ l ]<br />
d<br />
✍✌<br />
L t1 S<br />
R [1 − µr ]<br />
d<br />
✍✌<br />
FIG. <strong>3.</strong>42: Dominance in a Signaling <strong>Game</strong><br />
1<br />
2<br />
d<br />
<br />
1<br />
0<br />
<br />
0<br />
1<br />
<br />
2<br />
1<br />
<br />
0<br />
0<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 162 / 168
Analysis<br />
The following strategies and beliefs form a pooling equilibrium:<br />
[(L, L), (u, d), µl = 1<br />
2 , µr ≥ 1<br />
2 ]<br />
Because R is chosen with 0 probability in equilibrium, the belief µr can be<br />
chosen arbitrarily.<br />
But: For type t2 strategy R is strictly dominated, while it is not strictly<br />
dominated for type t1.<br />
Hence, Criterion <strong>3.</strong>1 requires that µr = 0. The pooling equilibria described<br />
above do not satisfy Criterion <strong>3.</strong>1.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 163 / 168
The Intuitive Criterion<br />
The Dominance Criterion rules out some equilibria but still not enough. The<br />
“Intuitive Criterion” that is due to Cho and Kreps (1987) goes much further.<br />
Consider the following signaling game:<br />
There are two types of senders:<br />
◮ a wimpy type: µ0 = 0.1<br />
◮ a surly type: 1 − µ0 = 0.9<br />
The receiver wants to fight the wimpy type but not the surly type.<br />
The sender can signal his type by the kind of breakfast he orders: Beer or<br />
Quiche.<br />
Payoffs are as follows:<br />
◮ Receiver gets 0 if he does not fight, 1 if he fights the wimpy type and -1 if he<br />
fights the surly type.<br />
◮ Sender: Both types prefer not to fight. The surly type prefers Beer for<br />
breakfast, the wimpy type prefers Quiche. The preferred breakfast gives an<br />
additional payoff of 1, not having to fight increases the payoff by 2.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 164 / 168
1<br />
1<br />
<br />
3<br />
0<br />
<br />
0<br />
−1<br />
<br />
2<br />
0<br />
✎☞<br />
✎☞<br />
f<br />
[µq]<br />
. .. . <br />
wimpy S<br />
Quiche t1 <br />
Beer<br />
[µ b]<br />
. <br />
f<br />
n<br />
f<br />
0, 1<br />
R Nature R<br />
0, 9<br />
.<br />
.. . . <br />
. <br />
[1 − µq] Quiche<br />
n<br />
✍✌<br />
t2 surly S<br />
Beer [1 − µ b]<br />
n<br />
✍✌<br />
FIG. <strong>3.</strong>43: The “Beer-Quiche” <strong>Game</strong><br />
Consider the following pooling equilibria:<br />
<br />
(Quiche, Quiche), (n, f ), µq = 0.1, µb ≥ 1<br />
<br />
2<br />
n<br />
f<br />
<br />
0<br />
1<br />
<br />
2<br />
0<br />
<br />
1<br />
−1<br />
<br />
3<br />
0<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 165 / 168
Analysis<br />
Along the equilibrium path both types eat Quiche and there is no fight. If<br />
the receiver observes “Beer”, however, he believes that the probability of<br />
the surly type is lower than 0.5 and fights.<br />
These equilibria satisfy the Dominance Criterion <strong>3.</strong>1, because “Beer” is<br />
not strictly dominated for either type.<br />
Suppose that the sender after drinking his beer gives the following<br />
speech to the receiver:<br />
“Dear Receiver, the fact that I had Beer for breakfast should convince you<br />
that I am the surly type:<br />
◮ If I was the wimpy type, I could not improve my situation by drinking beer.<br />
Instead of my equilibrium payoff of 3 I would get either 0 or 2.<br />
◮ If I was the surly type, however, I could benefit. My payoff would increase<br />
from 2 to 3 if I manage to convince you that I am the surly type.<br />
Hence my deviation makes sense only if I am the surly type.”<br />
Would you be convinced by this speech? If so, you will also believe in the<br />
“Intuitive Criterion”.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 166 / 168
Criterion <strong>3.</strong>2 (Intuitive Criterion)<br />
Consider a PBE (m ∗ , a ∗ ) of a signaling game. If the information set that is<br />
reached after message ˜m has been sent is off the equilibrium path, and if<br />
message ˜m is equilibrium dominated for type i, i.e., if<br />
U S (ti, m ∗ (ti), a ∗ (m ∗ (ti))) ≥ maxa∈AU S (ti, ˜m, a) ,<br />
then the receiver should assign probability 0 to type i of the sender, provided<br />
that there exists at least one other type tj for whom ˜m is not equilibrium<br />
dominated.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 167 / 168
Remarks:<br />
1. The Intuitive Criterion compares the highest possible payoff when ˜m is<br />
sent not with the lowest possible payoff that type ti could have received<br />
by sending another message, but rather with the payoff that type ti gets in<br />
equilibrium. This is much more demanding than Criterion <strong>3.</strong>1.<br />
2. Criterion <strong>3.</strong>2 implies Criterion <strong>3.</strong>1. Why?<br />
<strong>3.</strong> The Intuitive Criterion assumes some sort of hyperrationality: If there is a<br />
deviation from the equilibrium path, then the player should try to<br />
“rationally” explain this deviation. This is in stark contrast to the trembling<br />
hand story. Cho and Kreps show that every signaling game has at least<br />
one PBE satisfying the Intuitive Criterion.<br />
In the next chapter we will consider an application of signaling games to labor<br />
markets.<br />
Klaus M. <strong>Schmidt</strong> (<strong>LMU</strong> Munich) <strong>3.</strong> <strong>Game</strong> <strong>Theory</strong> Micro (Research), Winter 2011/12 168 / 168