Measuring Market Risk - Reserve Bank of India

MEASURING MARKET RISK 21
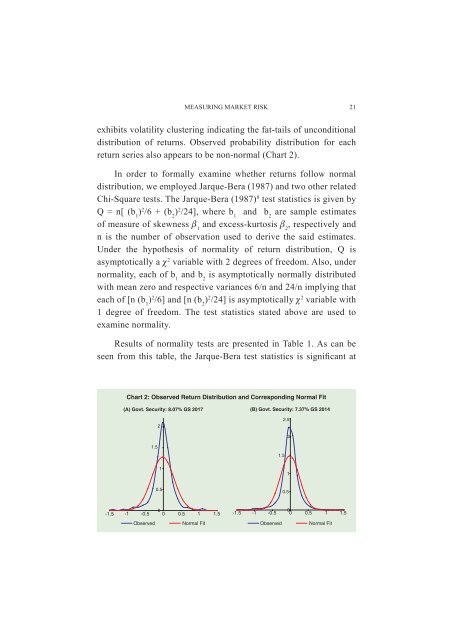
exhibits volatility clustering indicating the fat-tails of unconditional
distribution of returns. Observed probability distribution for each
return series also appears to be non-normal (Chart 2).
In order to formally examine whether returns follow normal
distribution, we employed Jarque-Bera (1987) and two other related
Chi-Square tests. The Jarque-Bera (1987) 8 test statistics is given by
Q = n[ (b 1
) 2 /6 + (b 2
) 2 /24], where b 1
and b 2
are sample estimates
of measure of skewness β 1
and excess-kurtosis β 2
, respectively and
n is the number of observation used to derive the said estimates.
Under the hypothesis of normality of return distribution, Q is
asymptotically a χ 2 variable with 2 degrees of freedom. Also, under
normality, each of b 1
and b 2
is asymptotically normally distributed
with mean zero and respective variances 6/n and 24/n implying that
each of [n (b 1
) 2 /6] and [n (b 2
) 2 /24] is asymptotically χ 2 variable with
1 degree of freedom. The test statistics stated above are used to
examine normality.
Results of normality tests are presented in Table 1. As can be
seen from this table, the Jarque-Bera test statistics is significant at