Measuring Market Risk - Reserve Bank of India

MEASURING MARKET RISK 25
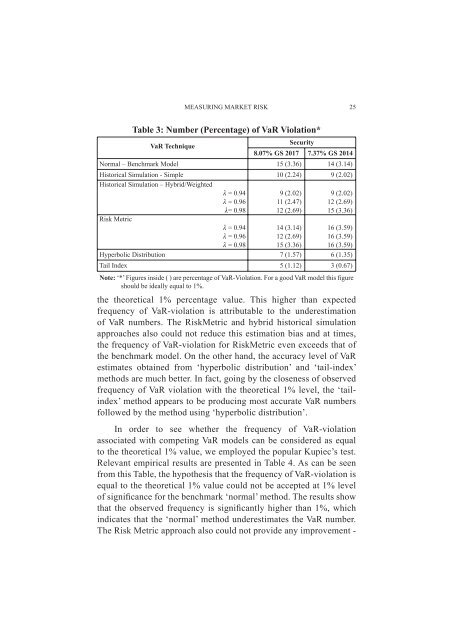
Table 3: Number (Percentage) of VaR Violation*
VaR Technique
Security
8.07% GS 2017 7.37% GS 2014
Normal – Benchmark Model 15 (3.36) 14 (3.14)
Historical Simulation - Simple 10 (2.24) 9 (2.02)
Historical Simulation – Hybrid/Weighted
λ = 0.94 9 (2.02) 9 (2.02)
λ = 0.96 11 (2.47) 12 (2.69)
λ= 0.98 12 (2.69) 15 (3.36)
Risk Metric
λ = 0.94 14 (3.14) 16 (3.59)
λ = 0.96 12 (2.69) 16 (3.59)
λ = 0.98 15 (3.36) 16 (3.59)
Hyperbolic Distribution 7 (1.57) 6 (1.35)
Tail Index 5 (1.12) 3 (0.67)
Note: ‘*’ Figures inside ( ) are percentage of VaR-Violation. For a good VaR model this figure
should be ideally equal to 1%.
the theoretical 1% percentage value. This higher than expected
frequency of VaR-violation is attributable to the underestimation
of VaR numbers. The RiskMetric and hybrid historical simulation
approaches also could not reduce this estimation bias and at times,
the frequency of VaR-violation for RiskMetric even exceeds that of
the benchmark model. On the other hand, the accuracy level of VaR
estimates obtained from ‘hyperbolic distribution’ and ‘tail-index’
methods are much better. In fact, going by the closeness of observed
frequency of VaR violation with the theoretical 1% level, the ‘tailindex’
method appears to be producing most accurate VaR numbers
followed by the method using ‘hyperbolic distribution’.
In order to see whether the frequency of VaR-violation
associated with competing VaR models can be considered as equal
to the theoretical 1% value, we employed the popular Kupiec’s test.
Relevant empirical results are presented in Table 4. As can be seen
from this Table, the hypothesis that the frequency of VaR-violation is
equal to the theoretical 1% value could not be accepted at 1% level
of significance for the benchmark ‘normal’ method. The results show
that the observed frequency is significantly higher than 1%, which
indicates that the ‘normal’ method underestimates the VaR number.
The Risk Metric approach also could not provide any improvement -