Level MSc 2012/13 Civil Engineering - Swansea University
Level MSc 2012/13 Civil Engineering - Swansea University
Level MSc 2012/13 Civil Engineering - Swansea University
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
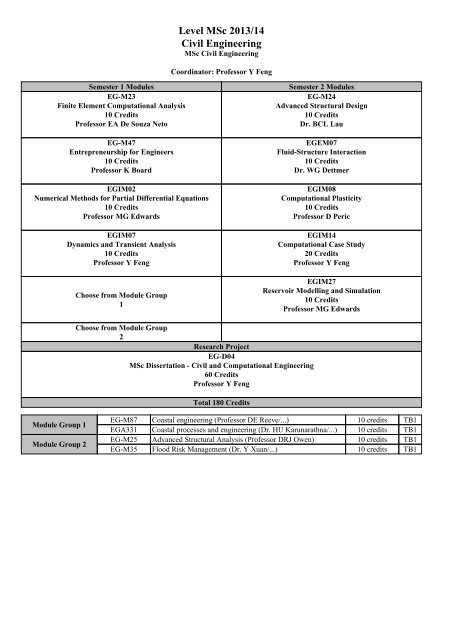
<strong>Level</strong> <strong>MSc</strong> 20<strong>13</strong>/14<br />
<strong>Civil</strong> <strong>Engineering</strong><br />
<strong>MSc</strong> <strong>Civil</strong> <strong>Engineering</strong><br />
Coordinator: Professor Y Feng<br />
Semester 1 Modules<br />
EG-M23<br />
Finite Element Computational Analysis<br />
10 Credits<br />
Professor EA De Souza Neto<br />
EG-M47<br />
Entrepreneurship for Engineers<br />
10 Credits<br />
Professor K Board<br />
EGIM02<br />
Numerical Methods for Partial Differential Equations<br />
10 Credits<br />
Professor MG Edwards<br />
EGIM07<br />
Dynamics and Transient Analysis<br />
10 Credits<br />
Professor Y Feng<br />
Choose from Module Group<br />
1<br />
Semester 2 Modules<br />
EG-M24<br />
Advanced Structural Design<br />
10 Credits<br />
Dr. BCL Lau<br />
EGEM07<br />
Fluid-Structure Interaction<br />
10 Credits<br />
Dr. WG Dettmer<br />
EGIM08<br />
Computational Plasticity<br />
10 Credits<br />
Professor D Peric<br />
EGIM14<br />
Computational Case Study<br />
20 Credits<br />
Professor Y Feng<br />
EGIM27<br />
Reservoir Modelling and Simulation<br />
10 Credits<br />
Professor MG Edwards<br />
Choose from Module Group<br />
2<br />
Research Project<br />
EG-D04<br />
<strong>MSc</strong> Dissertation - <strong>Civil</strong> and Computational <strong>Engineering</strong><br />
60 Credits<br />
Professor Y Feng<br />
Total 180 Credits<br />
Module Group 1<br />
Module Group 2<br />
EG-M87 Coastal engineering (Professor DE Reeve/...) 10 credits TB1<br />
EGA331 Coastal processes and engineering (Dr. HU Karunarathna/...) 10 credits TB1<br />
EG-M25 Advanced Structural Analysis (Professor DRJ Owen) 10 credits TB1<br />
EG-M35 Flood Risk Management (Dr. Y Xuan/...) 10 credits TB1
EG-D04 <strong>MSc</strong> Dissertation - <strong>Civil</strong> and Computational <strong>Engineering</strong><br />
Credits: 60 Session: 20<strong>13</strong>/14 Summer (July - September Modular)<br />
Module Aims: The module aims to develop fundamental research skills. It comprises the development of supervised<br />
research work leading to a dissertation in the field of the Master's degree programme. The specific research topic will<br />
be chosen by the student following consultation with academic staff.<br />
Pre-requisite Modules:<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format:<br />
Typically 1 hour per week i.e 10-15 hrs total contact time. Each student is to be supervised in<br />
accordance with the <strong>University</strong>’s Policy on Supervision, with a minimum of three meetings held. A<br />
careful record should be kept, agreed between supervisor and student, of all such formal meetings,<br />
including dates, action agreed and deadlines set.<br />
Lecturer(s): Professor Y Feng<br />
Assessment: Other (Coursework) (100%)<br />
Assessment Description: The research project and dissertation forms Part Two of the Masters degree. Information<br />
about dissertation preparation and submission can be found at:<br />
http://www.swan.ac.uk/registry/academicguide/assessmentandprogress/dissertationpreparationsubmission/<br />
Additionally, students should refer to:<br />
http://www.swan.ac.uk/registry/academicguide/postgraduatetaughtawardsregulations/postgraduatetaughtmastersdegre<br />
es/17submissionofdissertation/<br />
The word limit is 20,000. This is for the main text and does not include appendices (if any), essential footnotes,<br />
introductory parts and statements or the bibliography and index.<br />
Each student is to submit two soft bound copies and an electronic copy of the dissertation (CD with dissertation in Pdf<br />
format) to the College Postgraduate Administration Team by the deadline of 30th September. Each copy must contain:<br />
• a statement that it is being submitted in partial fulfilment of the requirements for the degree;<br />
• a summary of the dissertation not exceeding 300 words in length;<br />
• a statement, signed by you, showing to what extent the work submitted is the result of your own investigation.<br />
Acknowledgement of other sources shall be made by footnotes giving explicit references. A full bibliography should<br />
be appended to the work;<br />
• a declaration, signed by you, to certify that the work has not already been accepted in substance for any degree,<br />
and is not being concurrently submitted in candidature for any degree; and<br />
• a signed statement regarding availability of the thesis.<br />
The dissertation is marked by the supervisor and another member of staff and sent to an External Examiner for<br />
moderation. An Internal Exam Board is then held to confirm the mark. Finally, all marks are ratified at the <strong>University</strong><br />
Postgraduate Taught Examination Board.<br />
Failure Redemption: Candidates who fail the dissertation are given an opportunity to resubmit the dissertation within<br />
3 months of the result of the examination if a full-time student or 6 months for part-time students. Such students will<br />
be given one formal feedback session, including written feedback on the reasons for failure, immediately following<br />
confirmation of the result by the <strong>University</strong> Postgraduate Taught Examination Board. The opportunity to resubmit will<br />
only be offered to students who submit a dissertation and are awarded a fail. Those candidates who do not submit a<br />
dissertation will not be offered a resubmission opportunity.<br />
Assessment Feedback: Informal feedback will be given during regular meetings with supervisors. The supervisor<br />
will also provide an assessment of the project drafting skills during the planning of the dissertation. Work will be<br />
returned according to specified deadlines and accompanied by constructive comment.<br />
A Feedback session will be given to any student who fails their dissertation and is permitted by the Award Board to<br />
resubmit their work.
Module Content: Study for the dissertation, which may be based on practical, industrial, or literature work, or any<br />
combination of these, is primarily carried out over a period of about 12 weeks, with the dissertation being submitted at<br />
the end of September. Preparatory work on the dissertation may take place during Part One of the programme but<br />
students will only be permitted to submit their dissertation following successful completion of Part One.<br />
In conducting the research project and dissertation the student will be exposed to all aspects of modern information<br />
retrieval processes, the organisation and resourcing of research and the organising and presentation of experimental<br />
data. The student must make inferences on conclusions, based on the evidence provided and supported by the research<br />
work. Furthermore they must assess the significance of this work in relation to the field and make suggestions about<br />
how further work could improve or clarify the research problem. The results of the project will be disseminated in a<br />
substantial dissertation demonstrating the student's ability to research a subject in depth.<br />
The student will meet regularly with the supervisor to ensure that the project is well developed and organised.<br />
Progress will be monitored.<br />
Intended Learning Outcomes: On completion of this module, students should have the ability to:<br />
• investigate a research topic in detail;<br />
• formulate research aims;<br />
• devise and plan a research strategy to fulfil the aims;<br />
• carry out research work - undertake a literature search, a laboratory based or computer based investigation or a<br />
combination of these;<br />
• gather, organize and use evidence, data and information from a variety of primary and secondary sources;<br />
• critically analyse information;<br />
• make conclusions supported by the work and identify their relevance to the broader research area;<br />
• resolve or refine a research problem, with reasoned suggestions about how to improve future research efforts in the<br />
field; and<br />
• produce a report (dissertation), with the findings presented in a well organised and reasoned manner.<br />
Reading List:<br />
Additional Notes: The College of <strong>Engineering</strong> has a ZERO TOLERANCE penalty policy for late submission of all<br />
coursework and continuous assessment.<br />
If an extension is deemed appropriate a Postgraduate Taught Masters ‘Application for Extension to the Submission<br />
Deadline/ Period of Candidature’ Form will need to be submitted as follows:<br />
• 31 August – deadline for Part Two students (non-resit students)<br />
• 8 November – deadline for Part Two Students (students who had resits)
EG-M23 Finite Element Computational Analysis<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: This module introduces the fundamentals of the Finite Element Method to enable the student to use it<br />
in the solution of a range of problems of engineering interest. The classes of engineering problems covered in this<br />
module include elastic analysis of structures, heat conduction problems, seepage flow through soils and ideal fluid<br />
flow. In this context, the MATLAB programming language is used to create computer programs capable of solving<br />
these classes of problems.<br />
Pre-requisite Modules:<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format:<br />
Lectures 2h per week<br />
Example Classes 1h per week<br />
Directed private study 3h per week<br />
Lecturer(s): Professor EA De Souza Neto<br />
Assessment: Examination 1 (75%)<br />
Assignment 1 (25%)<br />
Assessment Description: Examination - Standard university examination (open book) worth 75% of the module<br />
marks.<br />
Assignment - Individual programming (MATLAB) assignment where students are required to produce an FE-related<br />
code based on the theory given in class. The assignment is worth 25% of the total marks for this module.<br />
Failure Redemption: Exam re-sits according to university regulations. A supplementary exam will form 100% of the<br />
module marks.<br />
Assessment Feedback: Examination - Standard university exam feedback form.<br />
Assignment - Comments on submitted work will be emailed to students.<br />
Module Content: Weighted residual methods for differential equations in 1-D, the Galerkin Method. [2]<br />
Ritz-Rayleigh variational Method in 1-D, Augmented Ritz functional. [1]<br />
Galerkin-based FE methods in 1-D. [2]<br />
1-D elasticity and steady-state heat transfer. Ritz-Rayleigh approach to FE [1]<br />
Quadratic Lagrangian finite elements in 1-D. [2]<br />
2-D quasi-harmonic problems. FE solution [3]<br />
2-D and axisymmetric elasticity. FE solution [2]<br />
FE solution of 3D elasticity problems [1]<br />
Numerical integration, Gaussian quadratures [1]<br />
Isoparametric finite elements [2]<br />
FE programming using MATLAB [3]<br />
Intended Learning Outcomes: Students should be able to demonstrate a knowledge and understanding of:<br />
Weighted residual methods for the solution of differential equations. The Finite Element Method for solution of linear<br />
problems in elastostatics and quasi-harmonic problems. The approximations involved in a Finite Element model.<br />
An ability to (thinking skills): Convert a realistic elasticity, heat conduction, seepage flow and ideal fluid flow<br />
engineering problems into FE models. Solve simple elasticity, heat transfer, seepage flow and ideal fluid flow<br />
problems by hand using the FE method. Identify the key issues to be considered when performing computational<br />
simulations of simple engineering problems.<br />
An ability to (practical skills): Use a computer program to set up and produce FE solutions of simple engineering<br />
problems. Analyse/assess the output of FE simulations. Produce simple FE-related code in MATLAB computer<br />
language.<br />
Reading List: T.P. Chandrupatla & A.D. Belegundu, (R) Introduction to Finite Elements in <strong>Engineering</strong>, Prentice-<br />
Hall, 2002.<br />
Hinton and D.R.J. Owen, (R) An introduction to finite element computations , Pineridge Press, 1979.<br />
D.J. Henwood & J. Bonet, (R) Finite Elements - A Gentle Introduction, Macmillan, 1997.<br />
J Fish & T Belytschko, A First Course in Finite Elements, John Wiley & Sons, 2007.ISBN: 0470035803
Additional Notes: Penalty for late submission of continual assessment assignment: No marks awarded for late<br />
submissions.<br />
Available to visiting and exchange students.<br />
This module requires a prior knowledge of computer programming - more specifically, MATLAB programming<br />
language - at a fairly basic level.
EG-M24 Advanced Structural Design<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 2 (Jan - Jun Modular)<br />
Module Aims: This module aims to equip students with advanced structural design concepts from first principles,<br />
such as yield line theory, prestressed beams, combined torsion, bending and shear, strut and tie, composite sections,<br />
fire engineering. Design of sustainability and its applications will be taught. The module is taught in accordance with<br />
structural Eurocodes.<br />
Pre-requisite Modules: EG-222; EG-225; EG-328<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format: Lectures 24 hours. Example classes 9 hours. Directed private study 33 hours.<br />
Lecturer(s): Dr. BCL Lau<br />
Assessment: Examination 1 (80%)<br />
Assignment 1 (20%)<br />
Assessment Description: Assessment: 20% of marks from the assigned design project work. Remaining 80% of the<br />
module marks are obtained by means of a 2-hour end of teaching block Closed Book examination.<br />
This module operates on a zero tolerance policy for late submission/plagiarism/collusion/commissioning of<br />
coursework i.e. zero marks awarded.<br />
Failure Redemption: Exam re-sits according to university regulations.<br />
Normally, a supplementary examination will form 100% of the module mark.<br />
Assessment Feedback: Individual oral or written feedback will be given on coursework, prior to the January<br />
examination. Examination feedback will be provided via the College of <strong>Engineering</strong> online feedback system,<br />
reflecting on the class performance as a whole to individual exam questions.<br />
Module Content: Module content:<br />
Concrete Design to BS EN 1992<br />
- Prestressed concrete beams design [3]<br />
- Plastic analysis and design of reinforced concrete slabs, yield line theory and finite element method for analysis of<br />
slab[3]<br />
- Design of torsion with combination of shear in reinforced concrete structures [2]<br />
- Strut and tie analysis [2]<br />
Steel Design to BS EN 1993, 1994<br />
- Structural analysis of steelwork - global analysis, P-deta effect, imperfection [2]<br />
- Design of steel-concrete composite plate girders - effective length, shear connectors, differential shrinkage effect [5]<br />
- Connections - haunch connection design and in-plane moment connection [3]<br />
- Fire engineering - fire resistance of steel structures [2]<br />
Sustainable design concepts and their applications [2]<br />
Intended Learning Outcomes: After completing this module you should be able to demonstrate:<br />
a knowledge and understanding of: Advanced design theories, techniques and software for analysis and design of<br />
complicated reinforced concrete, prestressed concrete, steel structures and steel-concrete composite plate girders.<br />
Reading List: F. K. Kong, R. H. Evans, Reinforced and Prestressed Concrete, CRC Press, 1987.ISBN: 978-<br />
0419245605<br />
M. Lawrence, J. Purkiss, Structural Design of Steelwork to EN 1993 and EN 1994, Butterworth-Heinemann.ISBN:<br />
978-0-7506-5060-1<br />
S. S. J. Moy, Plastic Methods for Steel and Concrete Structures, Palgrave Macmillan, 1996.ISBN: 978-0333641774<br />
SCI, Steel Designer's Manual, Blackwell Publishing, <strong>2012</strong>.ISBN: 978-1405189408<br />
R.K Westbrook, Design Examples to EC3 Structural Steelwork, Pearson Higher Education & Professional.ISBN:<br />
05820<strong>13</strong>100<br />
J.H. Bungey, W.H. Mosley, R. Hulse, Reinforced Concrete Design to Eurocode 2 , Palgrave Macmillan.ISBN:<br />
0230500714<br />
Steel Design and Concrete Design Handbooks, The Institution of Structural Engineers.
Additional Notes: This module particularly builds on the work of <strong>Level</strong> 3 structural design and mechanics modules<br />
EG-328 and EG-320. Therefore it may not be suitable for visiting and exchange students, unless student has prior<br />
knowledge of structural analysis and design equivalent to modules EG-328 and EG-320. Similarly, students entering<br />
directly to <strong>Level</strong> 4 <strong>Civil</strong> <strong>Engineering</strong> should familiarise themselves with the content of those <strong>Level</strong> 3 modules as soon<br />
as possible.
EG-M25 Advanced Structural Analysis<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: The module develops theory and associated solution techniques relevant to structural problems related<br />
to plates, shells and solid applications. The basic theoretical concepts are firstly introduced and the underlying<br />
governing equations then developed. The first topic considered is the elastic theory of plate bending analysis, which is<br />
of fundamental importance in the design and analysis of a large class of engineering structures. This is followed by the<br />
limit analysis of plate structures, which is of prominence in reinforced concrete design. A central aspect of the course<br />
is the treatment of the membrane analysis of shell structures. Most shell structures operate by their resistance to<br />
membrane action, rather than bending, and the course develops solution procedures for a range of practical<br />
applications encountered in both civil and mechanical engineering environments. The course concludes by developing<br />
solution strategies for structures subjected to torsion, with particular emphasis placed on the analysis of closed thin<br />
walled structures, such as those encountered in bridge deck construction and aerospace applications.<br />
Pre-requisite Modules: EG-320<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format: Lectures 20 (h); Example classes 10 (h); Directed private study 70 (h)<br />
Lecturer(s): Professor DRJ Owen<br />
Assessment: Examination 1 (75%)<br />
Coursework 1 (25%)<br />
Assessment Description: Examination 1 - Standard 2 hour university examination worth 75% of the final mark. This<br />
is a closed book examination.<br />
Coursework 1 will contribute 25% of the final mark.<br />
Failure Redemption: Exam re-sits according to <strong>University</strong> regulations.<br />
Normally, a supplementary examination will form 100% of the module mark.<br />
Assessment Feedback: Standard engineering exam feedback form plus feedback on coursework. Example classes are<br />
also provided to enhance student understanding during the course.<br />
Module Content: Introduction to the flexural behaviour of plates. Equilibrium conditions and the development of the<br />
governing equation for plate bending in terms of bending moments. [2]<br />
Compatibility conditions. Constitutive laws and the moment/curvature relations. The governing equation in terms of<br />
displacements. [2]<br />
Boundary conditions for rectangular plates. Navier's solution for simply supported rectangular plates. [2]<br />
Point loaded simply supported rectangular plates. Development of the governing equations for axisymmetrically<br />
loaded circular plates. [2]<br />
Solution of axisymmetrically loaded circular plate problems. Introduction to the limit analysis of reinforced concrete<br />
slabs. [2]<br />
Principle of virtual work method and equilibrium method for the evaluation of limit loads of slabs. Problem solution<br />
involving orthotropically reinforced slabs. [2]<br />
Introduction to shell behaviour. The theory of shell action under membrane behaviour. [2]<br />
The solution of a range of engineering problems involving axisymmetrically loaded shells of revolution. [2]<br />
Theory of unsymmetrically loaded shells of revolution. Solution of engineering examples. [2]<br />
Introduction to prestressed concrete. Uniformly prestressed sections - theory and numerical examples. [2]<br />
Eccentrically prestressed sections - theory and numerical examples. Statically indeterminate systems. Evaluation of<br />
concordant tendon profiles. [2]<br />
Revision. [2]
Intended Learning Outcomes: Should be able to demonstrate a knowledge and understanding of:<br />
The principles of equilibrium, compatibility and the influence of material behaviour. Virtual Work expressions of<br />
equilibrium and compatibility and the Unit Load Theorem.<br />
An ability to (thinking skills): Identify the forces applied by various supports. Distinguish between axial, bending,<br />
shear and torsional load carrying actions. Distinguish between statically determinate and indeterminate structures.<br />
Identify appropriate methods of analysis for trusses, beams and frames.<br />
An ability to (practical skills): Apply the equations of static equilibrium to calculate reactions, axial forces, bending<br />
moments, shear forces and torsional forces. Use the Unit Load Method for the calculation of displacements and<br />
rotations in structures. Analyse simple externally indeterminate 2-dimensional structures. Apply the Moment<br />
Distribution Method to the analysis of statically indeterminate beams. Use a computer to model and analyse trusses,<br />
beams and frames.<br />
An ability to (key skills): Use a personal computer. Study independently and use library resources. Effectively take<br />
notes and manage working time.<br />
Reading List: Timoshenko, Theory of Plates and Shells, McGraw Hill.<br />
Timoshenko, Theory of Elasticity, McGraw Hill.<br />
Additional Notes: Not available to visiting and exchange students.<br />
Failure to sit an examination or submit work by the specified date will result in a mark of 0% being recorded.<br />
This module particularly builds on the work you have done in the <strong>Level</strong> 2 Structural Mechanics 2 (a) and (b) modules<br />
as well as <strong>Level</strong> 3 Structural Mechanics 3. You should revise the topics learnt in these modules. This module also<br />
assumes that you are familiar with the basic mathematical concepts learnt in the <strong>Level</strong>s 1 and 2 mathematics modules.<br />
Office hours will be posted up on the notice board outside Room 175 (Prof. D. R. J. Owen)
EG-M35 Flood Risk Management<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: Recent years have seen an increasingly volatile climate and hence severe floods across the UK and<br />
worldwide, which also accompanies with a constant demand for expertise and know-hows for flood risk management.<br />
We intend to use this module to facilitate civil and environmental engineering students with necessary engineering<br />
skills and techniques for flood risk management with special focuses on current practice and national polices related<br />
and climate change impact and sustainability issues. Any student wanting to pursue or develop in a related career, e.g.,<br />
water managers, consultancy in flood risk management is encouraged to take the module.<br />
Pre-requisite Modules: EG-329<br />
Co-requisite Modules: EG-M87<br />
Incompatible Modules:<br />
Format:<br />
Lectures 20 hours;<br />
Example classes 10 hours;<br />
Directed private study 20 hours;<br />
Private study 40 hours;<br />
Preparation for assessment: 10 hours.<br />
Lecturer(s): Dr. Y Xuan, Dr. HU Karunarathna, Professor DE Reeve<br />
Assessment: Coursework 1 (30%)<br />
Examination 1 (70%)<br />
Assessment Description: Coursework 1: written coursework counts to 30% of total marks. Zero tolerance for late<br />
submission.<br />
Examination 1: written exam counts to 70% of total marks. Closed-book exam taking place in January.<br />
Examination 2: closed-book, written exam of rest.<br />
Failure Redemption: Exam resits according to university regulation.<br />
A supplementary examination will form 100% of the module mark.<br />
Assessment Feedback: Coursework: students will receive feedback via Blackboard according to university<br />
regulation.<br />
Examination: feedback will be provided using standard university exam feedback form.<br />
Module Content: 1. Introduction to flood risk management: concepts and approaches [0.5]<br />
2. Water systems and hydrometrics[0.5]<br />
3. Water system modeling for flood risk management[3]:<br />
3.1 Fluvial flooding: transfer function, lumped model, distributed model, hydraulic models<br />
3.2 Urban flooding: urban drainage and sewer modelling<br />
3.3 Flood estimation over ungagged catchment: FEH method<br />
3.4 Storm surge and overtopping<br />
3.5 Coastal and estuary flooding.<br />
4. Flood risk, extreme value and reliability analysis [1]<br />
4.1 Probability theory and its application in flood risk management<br />
4.2 Design Flood and PMP, PMF<br />
4.3 Extreme value theory and reliability analysis.<br />
5. FRM Planning, flood hazard and inundation maps. [1]<br />
6 Flood forecasting/Warning and communication systems [1]<br />
7. Options and measures for flood risk management [1]<br />
7.1 UK and EU Policies and Practices<br />
7.2 Prevention, mitigation measures and insurance<br />
7.3 Sustainability issues.<br />
8. Global environment change impact on flood risk and resilience [2]<br />
8.1 Climate change impact<br />
8.2 Land use change impact<br />
8.3 Adaptation and resilience building measures.
Intended Learning Outcomes: Upon completion of the module, students are expected to be able to:<br />
1. understand and demonstrate the concept of flood risk management, relevant policies of the UK and EU;<br />
2. understand and be acquainted with the necessary modelling techniques for flood forecasting and flood risk<br />
management;<br />
3. use FEH method to estimate flood for ungauged catchment;<br />
4. be accustomed to GIS and use GIS tools to produce flood hazard map and/or analysis;<br />
5. understand and demonstrate the use of probability (extreme value) theory for flood risk analysis;<br />
6. establish and enhance the awareness of the sustainability issues in flood risk management;<br />
7. understand the climate change and other global change impacts on flood risk management;<br />
8. demonstrate the readiness for progressing to relevant profession.<br />
Reading List:<br />
Additional Notes: Available to visiting and exchange students.
EG-M47 Entrepreneurship for Engineers<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: To establish the principles of entrepreneurship and the role engineers have in successful business<br />
enterprises.<br />
Pre-requisite Modules:<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format:<br />
Lectures 20 hours<br />
Example classes / Laboratory work 10 hours<br />
Directed private study 76 hours<br />
Lecturer(s): Professor K Board<br />
Assessment: Group Work - Coursework (80%)<br />
Coursework 1 (20%)<br />
Assessment Description: The group assignment will require application of the concepts of entrepreneurship. The<br />
assignment will require the delivery of a presentation and the submission of a business plan.<br />
The individual assignment will consist of a 600 word essay.<br />
Failure Redemption: 100% coursework.<br />
Assessment Feedback: Mainly through the group interviews held at the end of the course.<br />
Module Content: What is an entrepreneur and why enterprise matters; the six dimensions of entrepreneurship,<br />
structure and presentation of opportunities, sources and structure of finance, people and teams.<br />
How enterprise is managed internationally, managing early and long-term growth, harvesting and buy-out, sustaining<br />
the flow of ideas within a company, case-studies.<br />
Intended Learning Outcomes:<br />
After completing this module you should be able to:<br />
• Describe how opportunities are identified and a business plan is generated in order to get started<br />
• List the sources of finance that exist and how they are structured<br />
• Analyse the role of people and what makes a winning team<br />
• Discuss a case history that lead to success<br />
• Explain how early growth is managed<br />
• Analyse how failure can occur and how to guard against it<br />
• Explain how enterprise can be sustained within an organisation as it grows<br />
Reading List: Birley and Muzyka, Mastering Enterprise, Financial Times Publication, 1997.ISBN: 027363031<br />
Bridge, O'Neill and Martin, Understanding Enterprise, Entrepreneurship and Small Business, Palgrave Macmillan,<br />
2008.ISBN: 0230552706<br />
Additional Notes: The College of <strong>Engineering</strong> has a ZERO TOLERANCE penalty policy for late submission of all<br />
coursework and continuous assessment<br />
Related assignments are used to assess this module.
EG-M87 Coastal engineering<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: This is the main module on the subject of coastal engineering. The module provides the background<br />
for undertaking detailed design of coastal flood defences and coastal protection schemes. It includes wider issues such<br />
as: the coastal planning regime in the UK; the impacts of climate change on design; sustainability of coastal defences;<br />
assessing flood risk. The programme will consist of a series of lectures and examples classes to study instances of<br />
coastal environments &/or engineering schemes.<br />
Pre-requisite Modules: EGA331<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format:<br />
Lectures 2 hours/week<br />
Example classes 1hour/week<br />
Directed private study 4 hours per week<br />
Lecturer(s): Professor DE Reeve, Dr. HU Karunarathna<br />
Assessment: Coursework 1 (20%)<br />
Coursework 2 (20%)<br />
Examination 1 (60%)<br />
Assessment Description: Coursework 1 - written assessment on design wave specification (20%)<br />
Coursework 2 - written conceptual design assessment (20%)<br />
Exam (60%) closed book.<br />
Failure Redemption: A supplementary examination will form 100% of the module mark. Closed book.<br />
Assessment Feedback: Feedback on coursework via written comments and comments in class<br />
Feedback on exam via normal procedure; in subsequent years via overview of generic issues arising from previous<br />
examinations<br />
Module Content: Indicative syllabus -<br />
Introduction: conceptual design for coastal defence; sustainable shoreline management in the UK; overview of design<br />
process<br />
Design wave specification: Characteristics of wind waves and swell; concept of a random sea. Time and frequency<br />
domain parameters, Rayleigh distribution, energy and directional spectra. Introduction to principles of frequency<br />
analysis.<br />
Wave transformation: Refraction, shoaling and diffraction of monochromatic waves and directional spectra.<br />
Water level variations: tides and surge.<br />
Flood defences: Types & materials (embankments, revetments and seawalls); wave overtopping; formulae and<br />
methods; design criteria.<br />
Coastal protection: Types & materials (revetments, groynes, breakwaters); soft engineering options (renourishment,<br />
recycling); beach modelling.<br />
Reliability & risk: flood risk assessment.<br />
Intended Learning Outcomes: Demonstrate a knowledge and understanding of:<br />
*Conceptual design for coastal defence<br />
* Shoreline management process within the UK<br />
* Main elements of detailed design of coastal flood defences<br />
* The main options for coastal protection schemes<br />
* Sustainability and 'Soft' engineering options and methods<br />
Reading List: D. Reeve, A. Chadwick, C. Fleming, Coastal engineering: Processses, theory and design practice, CRC<br />
Press, 2011.ISBN: 978-0415583534<br />
Additional Notes: A background knowledge of Coastal <strong>Engineering</strong>/Processes is assumed. The material covered in<br />
EGA331 provides this.
EGA331 Coastal processes and engineering<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: This module provides an introduction to the subject of coastal engineering. It provides an overview of<br />
the main physical processes that shape the coastal environment and the wider context of coastal engineering, together<br />
with the underlying tidal theory, wave transformation methods and sediment transport concepts. The programme will<br />
consist of a series of lectures and examples classes.<br />
Pre-requisite Modules: EG 201<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format:<br />
Lectures 2 hours/week<br />
Example classes 1hour/week<br />
Directed private study 4 hours per week<br />
Lecturer(s): Dr. HU Karunarathna, Professor DE Reeve<br />
Assessment: Coursework 1 (25%)<br />
Examination 1 (75%)<br />
Assessment Description: Coursework 1 - written submission (25%)<br />
Closed Book Examination (75%)<br />
Failure Redemption: Resits over summer period.<br />
Assessment Feedback: Feedback on coursework via written comments and comments in class<br />
Feedback on exam via normal procedure; in subsequent years via overview of generic issues arising from previous<br />
examinations<br />
Module Content: Introduction: historical context, the coastal environment, context of design, hard and soft<br />
engineering options for coastal defence and their effects on the coastal environment, concepts of sustainability in<br />
coastal management.<br />
Theory of tides: equilibrium tidal theory; classification of tides; tidal analysis; tidal prediction; dynamic theory of<br />
tides<br />
Linear wave theory: derivation of airy wave equations; water particle motions; approximations for 'deep' and 'shallow'<br />
water; energy, power and group velocity; refraction, shoaling, reflection, diffraction and breaking; wave-induced<br />
currents; set-up and set-down; nonlinear theories.<br />
Water level variations: tides; surge; sea level rise; tsunamis<br />
Concepts in sediment transport: basic concepts; cross-shore and longshore transport equations<br />
Intended Learning Outcomes: Demonstrate a knowledge and understanding of:<br />
*Equilibrium theory of tides; tidal analysis; tidal prediction methods; classification of tides; limitations of equilibrium<br />
theory<br />
* Linear wave theory; wave transformations including refraction, shoaling, reflection, diffraction and breaking; waveinduced<br />
currents; wave set-up, set-down; limitations of linear theory<br />
* Surge; causes and components<br />
* Tsunamis; causes, propagation, characteristics<br />
* Basic concepts in sediment transport; examples of cross shore transport and long shore transport equations<br />
Reading List: Reeve, Chadwick & Fleming, Coastal <strong>Engineering</strong>: Processes, theory and design practice, Spon press,<br />
<strong>2012</strong>.ISBN: 978-0-415-58353-4<br />
Additional Notes: Module code reserved by d.e.reeve on 21/05/<strong>2012</strong> 14:07:06
EGEM07 Fluid-Structure Interaction<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 2 (Jan - Jun Modular)<br />
Module Aims: The understanding and the computer simulation of fluid-structure interaction is of increasing<br />
importance in many areas of modern engineering including <strong>Civil</strong>, Mechanical, Medical, Chemical and Aerospace<br />
<strong>Engineering</strong>. This module covers the mechanics of fluid-structure interaction as well as the numerical strategies for<br />
the computer simulation of such problems. Various phenomena, including wing divergence, oscillating pipes, vortexinduced<br />
vibrations, galloping and flutter, are studied and different approaches to the computer simulation of fluidstructure<br />
interaction are discussed. In the context of the computational strategies, the focus is on solution methods for<br />
the coupled system of differential equations that describe the interaction between the fluid flow and the structure.<br />
Pre-requisite Modules:<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format: lectures and example classes: 3 hours per week; private study: 4 hours per week; revision: 30 hours<br />
Lecturer(s): Dr. WG Dettmer<br />
Assessment: Examination 1 (70%)<br />
Assignment 1 (5%)<br />
Assignment 2 (15%)<br />
Assignment 3 (10%)<br />
Assessment Description: Examination:<br />
This is a closed book examination. The examination forms 70% of the module mark.<br />
Assignment 1: Wing Divergence<br />
This is an individual piece of coursework. It is worth 5% of the module mark and has to be submitted in week 5.<br />
Assignment 2: Galloping<br />
This is an individual piece of coursework. It is worth 15% of the module mark and has to be submitted in week 8.<br />
Assignment 3: Gauss-Seidel Iteration<br />
This is an individual piece of coursework. It is worth 10% of the module mark and has to be submitted in week 10.<br />
Failure Redemption: A supplementary examination will form 100% of the module mark.<br />
Assessment Feedback: Feedback on the assignments will be given verbally during office hours.<br />
Module Content:<br />
Fluid-Structure Interaction and Aeroelasticity:<br />
lift and drag forces, pitching moment,<br />
wing divergence,<br />
added mass,<br />
oscillating pipes,<br />
ship roll,<br />
vortex-induced vibration, lock-in,<br />
galloping, flutter<br />
Computational Solution Strategies:<br />
basics of computational modelling of fluid flow and structural dynamics,<br />
interface modelling, weak and strong coupling,<br />
Gauss-Seidel iteration, relaxation, convergence, Aitken acceleration,<br />
monolithic and partitioned Newton-Raphson methods,<br />
staggered schemes<br />
Intended Learning Outcomes: By the end of this module, the students should be able to<br />
* assess the stability of fluid-structure interaction systems,<br />
* calculate critical flow velocities for simple systems,<br />
* apply different computational solution strategies to simple problems,<br />
* assess the suitability of different solution strategies for a particular problem,<br />
* discretise time derivatives and resolve nonlinearities for small problems.<br />
Reading List: Blevins, Flow Induced Vibration, Van Nostrand Reinhold Company, 1977.ISBN: 1-57524-183-8
Additional Notes: The College of <strong>Engineering</strong> has a ZERO TOLERANCE penalty policy for late submission of all<br />
coursework and continuous assessment.<br />
Lecture notes, assignments and past examination papers will be available on Blackboard.
EGIM02 Numerical Methods for Partial Differential Equations<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: Introduction to numerical methods including ordinary and partial differential equations at masters<br />
level.<br />
Pre-requisite Modules: EG-189; EG-190; EG-399<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format:<br />
Lectures 20h<br />
Examples 10h<br />
Directed Private Study 70h<br />
Lecturer(s): Professor MG Edwards<br />
Assessment: Examination (70%)<br />
Assignment 1 (15%)<br />
Assignment 2 (15%)<br />
Assessment Description: Assessment is comprised of a closed book examination and 2 assignments involving<br />
analysis and computation.<br />
Failure Redemption: The supplementary closed book exam paper is sat during the month of August following the<br />
first exam sat in January.<br />
A supplementary examination will normally form 100% of the module mark and is capped at 50%.<br />
Assessment Feedback: Feedback on assessed work is given in example classes and via blackboard's gradecentre.<br />
Specific issues and questions are answered throughout the module including example classes.<br />
Feedback on formal examinations is given via web feedback template.<br />
Module Content: Review of Basic Numerical Methods and MATLAB commands.<br />
Overview of Numerical Modelling Techniques.<br />
Newtons method.<br />
Numerical Integration.<br />
Approximation of Ordinary and Partial differential equations.<br />
Finite difference and Finite volume methods for<br />
Elliptic, Parabolic and Hyperbolic partial differential equations.<br />
Consistency, stability and convergence.<br />
An Introduction to the Solution of Linear Systems.<br />
Gaussian elimination.<br />
Relaxation methods.<br />
Practical Work: Exercises/project will involve coding some of the methods presented in MATLAB<br />
Intended Learning Outcomes: Demonstrate a knowledge and understanding of:<br />
The basic principles of: numerical integration, numerical solution of ordinary and partial differential equations.<br />
Truncation error and solution error. Consistency, stability and convergence. Direct and iterative solution of Linear<br />
systems of equations.<br />
An ability to (thinking skills): Understand and formulate basic numerical procedures and solve illustrative problems.<br />
An ability to (practical skills): Understand practical implications of behaviour numerical methods and solutions.<br />
Logically formulate numerical methods for solution by computer with MATLAB.<br />
An ability to (key skills): Study independently, use library resources. Effectively take notes and manage working time.<br />
Reading List: Gerald and Wheatley, (R) Applied Numerical Analysis, -.<br />
Johnson and Riess , (R) Numerical Analysis, -.<br />
G. D. Smith, (R) Numerical Solution of Partial Differential Equations, Oxford <strong>University</strong> Press .<br />
Paul Du Chateau and D.W. Zachmann. , (F) Schaum's outline of partial differential equations , -.<br />
Additional Notes: Lecture notes provided.<br />
Failure to sit an examination or submit work by the specified date will result in a mark of 0% being recorded.
EGIM07 Dynamics and Transient Analysis<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 1 (Sep-Jan Modular)<br />
Module Aims: This module aims to develop the understanding and skills necessary to analyse linear structures under<br />
general dynamic, including earthquake loading, and to understand the use of time stepping schemes for linear dynamic<br />
and transient problems.<br />
Pre-requisite Modules: EG-260<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format: Lectures & Example classes (30h); Directed private study (30h)<br />
Lecturer(s): Professor Y Feng<br />
Assessment: Examination 1 (60%)<br />
Project (40%)<br />
Assessment Description: Formal lectures, example classes<br />
Failure Redemption: Redeem failed component in resit in August<br />
Assessment Feedback: Module feedback<br />
Module Content: Introduction: Dynamic effects on structures, <strong>Engineering</strong> disasters, design issues. [1]<br />
Single Degree of Freedom Problems: the SDOF spring-mass system, equivalent SDOF structures - energy method,<br />
analytical solution of SDOF problems, step by step solution methods, earthquake loading, response and design<br />
spectra, Eurocode- 8 elastic spectrum. [15]<br />
Multiple Degree of Freedom Problems: natural modes and frequencies of vibration, modal decomposition, reduction<br />
methods, earthquake loading, shear building model, design considerations. [9]<br />
Distributed Mass Systems: finite element discretization and formulations. [4]<br />
Revision [1]<br />
Intended Learning Outcomes: Students should be aware of possible disastrous consequences of structural failures<br />
under dynamic loadings, such as strong wind, wave and particularly earthquakes.<br />
Students should be able to demonstrate a knowledge and understanding of: Basic dynamic concepts of SDOF systems<br />
such as dynamic magnification, resonance, damping. The Rayleigh method for the simplification of complex<br />
structures to a SDOF system. Earthquake response and design spectra. Analytical and step-by-step integration<br />
methods for impulse and periodic forces. Modes of vibration and modal decomposition. Reduction methods. Mass<br />
damping. The shear building simplified model.<br />
Reading List: Chopra, Dynamics of structures, Prentice Hall.<br />
Clough & Penzien, Dynamics of Structures, McGraw-Hill.<br />
Dynamics - An Introduction for <strong>Civil</strong> & Structural Engineers, ICE (Design and Practice Guide).<br />
Additional Notes: Assessment: Written, open book, examination (2 hrs) at the end of Semester 1 accounts for 60% of<br />
the marks, the remaining 40% are awarded to an individual project, for which students are expected to solve a<br />
dynamical problem using Excel/Matlab etc and write a technical report on their findings. Penalty for late submission<br />
of course work is zero mark in the course work.<br />
Individual projects will be allocated during the course.<br />
Failure to sit an examination or submit work by the specified date will result in a mark of 0% being recorded.
EGIM08 Computational Plasticity<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 2 (Jan - Jun Modular)<br />
Module Aims: This module is concerned with basic concepts and methods of computational plasticity. Essential steps<br />
required in numerical integration of elasto-plastic constitutive models are first discussed in one-dimensional setting.<br />
Concepts of plasticity under multiaxial stress states are introduced and several yield criteria are described including<br />
von Mises, Tresca, Mohr-Coulomb and Drucker-Prager yield criteria. Details of numerical integration are provided for<br />
the von Mises yield criterion. Understanding of basic concepts and practical applications are strengthened through the<br />
programming exercises focusing on one-dimensional problems, and use of computational codes under multiaxial state<br />
of stress. Computer simulations of structural and geotechnical problems are performed, with the objective of<br />
understanding the concepts of engineering failure and limit state.<br />
Pre-requisite Modules:<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format: Lectures (20h); Example classes and Laboratory work (10h). Directed private study 3h per week.<br />
Lecturer(s): Professor D Peric<br />
Assessment: Examination 1 (50%)<br />
Assignment 1 (20%)<br />
Assignment 2 (30%)<br />
Assessment Description: Examination 1 - Standard 2 hour university examination worth 50% of the final mark. This<br />
is a closed book examination.<br />
The coursework will consist of two individual projects that will require both hand calculation and computer<br />
simulations. Computer simulation will require certain amount of programming and use of the existing finite element<br />
software package Elfen. The project reports should consist of two parts: (i) a discussion related to general aspects of<br />
formulation and computational treatment of the problem under consideration, (ii) description of numerical solution of<br />
an individual problem.<br />
Coursework 1 - Hand calculation and numerical solution in MATLAB will be used to obtain solution of simple 1-D<br />
elasto-plastic problem. Coursework 1 will contribute 20% of the final mark.<br />
Coursework 2 - Short hand calculation and computer simulation in commercial code will be used to obtain solution of<br />
a 2-D engineering problem. Coursework 2 will contribute 30% of the final mark.<br />
Failure Redemption: Exam re-sits according to university regulations.<br />
Normally, a supplementary examination will form 100% of the module mark.<br />
Assessment Feedback: Examination 1 - Standard university exam feedback form.<br />
Coursework 1 and 2 - Marked assignments with comments will be provided to students for inspection.<br />
Module Content: Introduction: Historical Perspective. Physical Motivation. Rate Independent Plasticity. Rate<br />
Dependence. Creep. Rheological Models. [2]<br />
1-D Mathematical Model: Yield Criterion. Flow Rule. Loading / Unloading Conditions. Isotropic and Kinematic<br />
Hardening Models. 1-D Elasto-Plastic Boundary Value Problem. [1]<br />
Computational Aspects of 1-D Elasto-Plasticity: Integration Algorithms for 1-D Elasto-Plasticity. Operator Split.<br />
Return Mapping. Incremental Elasto-Plastic BVP. Consistent Tangent Modulus. [5]<br />
Classical Model of Elasto-Plasticity: Physical Motivation. Classical Mathematical Model of Rate-Independent. Elasto-<br />
Plasticity: Yield Criterion. Flow Rule. Loading / Unloading Conditions. [6]<br />
Computational Aspects of Elasto-Plasticity: Integration Algorithms for Elasto-Plasticity. Operator Split. The Trial<br />
Elastic State. Return Mapping. Incremental Elasto-Plastic BVP. Consistent Tangent Modulus. [3]<br />
Plane Strain Von Mises Elasto-Plastic Model: Continuum. Integration Algorithm. Operator Split. The Trial Elastic<br />
State. Return Mapping; Incremental Elasto-Plastic BVP: Consistent Tangent Modulus. [4]<br />
Integration Algorithms for Generalised Elasto-Plasticity. [1]<br />
Generalisations and Applications of Plasticity: Plasticity in <strong>Engineering</strong> Practice: Geomechanics. Structural<br />
Mechanics. Impact Dynamics and Crashworthiness. [8]<br />
Intended Learning Outcomes: Students should be able to demonstrate:<br />
A knowledge and understanding of: Fundamentals of computational modelling of inelastic materials with emphasis on<br />
rate independent plasticity. A sound basis for approximation methods and finite element method, in particular.<br />
An ability to (thinking skills): Understand different methodologies for discretisation of different time evolution<br />
problems, and rate-independent elasto-plasticity in particular.<br />
An ability to (practical skills): Develop practical skills related to modelling of inelastic history dependent materials.<br />
Formulate and implement a computational procedure for integration of rate-independent elasto-plasticity in 1-D.<br />
Perform analysis of engineering problems in elasto-plasticity by employing a commercial finite element package.
Reading List: E. A. de Souza Neto, D. Peric and D. R. J. Owen, (R) Computational Methods for Plasticity: Theory<br />
and Applications, Wiley, 2008.ISBN: 978-0-470-69452-7<br />
J Lubliner, (F) Plasticity Theory, Dover, 2008.ISBN: 978-0486462905<br />
D R J Owen & E Hinton, (F) Finite Elements in Plasticity: Theory and Practice , Pineridge Press, 1980.ISBN: 0-<br />
906674-05-2<br />
J C Simo & T J R Hughes, (R) Computational Inelasticity, Springer, 1998.ISBN: 978-0387975207<br />
O C Zienkiewicz & R L Taylor, Inelastic and Non-linear Materials, Chapter 4 in The Finite Element Method for Solid<br />
and Structural Mechanics, Butterworth-Heinemann, 2005.ISBN: 978-0750663212<br />
M A Crisfield, Basic Plasticity, Chapter 6 of Non-Linear Finite Element Analysis of Solids and Structures. Volume 1:<br />
Introduction, Wiley, 1996.ISBN: 978-0471970590<br />
Additional Notes: Failure to attend activities that are a module requirement will normally mean that you cannot sit<br />
the final exam in the module.<br />
Zero tolerance will apply for late submissions of the assignments.<br />
Failure to sit an examination or submit work by the specified date will result in a mark of 0% being recorded.
EGIM14 Computational Case Study<br />
Credits: 20 Session: 20<strong>13</strong>/14 Semester 2 (Jan - Jun Modular)<br />
Module Aims: The aim of the module is to undertake an in-depth study into the use of computational methods in<br />
engineering practice by carrying out a detailed literature survey and state of the art examination in a given topic of<br />
specialisation.<br />
Pre-requisite Modules:<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format:<br />
No formal lectures invovled. Tutorials given by individual <strong>MSc</strong> research project supervisors (10h)<br />
Directed private study (190h)<br />
Lecturer(s): Professor Y Feng<br />
Assessment: Report (70%)<br />
Oral Examination (30%)<br />
Assessment Description: 1. Report: a formal report should be submitted before the deadline set-up by the supervisor,<br />
but normally around early May before the main exams start. The report will be marked by two examiners including<br />
the supervisor.<br />
2. Oral presentation: The student should give a 15-min presentation before two examiners and followed by Q & A.<br />
Failure Redemption: Students can resubmit the report and do the oral examination.<br />
Assessment Feedback: The student should be able to receive some feedback from the supervisor and the second<br />
examiner for the report, and can get direct feedback from the oral examination.<br />
Module Content: Literature review on chosen research topic.<br />
Familiarisation with chosen research topic.<br />
Planning of <strong>MSc</strong> thesis.<br />
Intended Learning Outcomes: The student should be able to demonstrate a knowledge and understanding of: The<br />
main aspects and state-of-the-art of the chosen <strong>MSc</strong> research topic; main problems and necessary steps to move<br />
forward in the chosen research topic.<br />
An ability to (thinking skills): Identify key aspects of a research topic.<br />
An ability to (practicalskills): Use web-based tools to perform bibliographic searches on a given topic.<br />
An ability to (key skills): Produce work to a deadline. Perform a bibliographic search on a given topic, select essential<br />
information for familiarisation with the subject. Plan research in advance.<br />
Reading List: Invertebrates, Sinauer Associates.<br />
Additional Notes: Around 5,000 word report on the chosen <strong>MSc</strong> research topic.<br />
Recommended Texts to be defined by supervisor according to the chosen research topic.<br />
Note: Dr Petar Igic is responsible for the candidates enrolled on <strong>MSc</strong> Electronics Technology for Sustainable Energy
EGIM27 Reservoir Modelling and Simulation<br />
Credits: 10 Session: 20<strong>13</strong>/14 Semester 2 (Jan - Jun Modular)<br />
Module Aims: subsurface reservoir modelling applies to petroleum reservoirs, aquifer remediation and carbon<br />
sequestration. This module provides an introduction to subsurface reservoir modelling at masters level.<br />
Pre-requisite Modules: EG-189; EG-190; EG-399; EG-399<br />
Co-requisite Modules:<br />
Incompatible Modules:<br />
Format: Lectures 20h; Examples 10h; Directed Private Study 70h<br />
Lecturer(s): Professor MG Edwards<br />
Assessment: Examination 1 (70%)<br />
Assignment 1 (15%)<br />
Assignment 2 (15%)<br />
Assessment Description: Closed book examination and 2 assignments involving analytical work and calculation.<br />
Failure Redemption: Supplementary closed book exam in the month of August following the first exam in<br />
May/June.<br />
Supplementary is normally a closed book exam marked out 100%, result capped at 50%.<br />
Assessment Feedback: Feedback on assessed work is given in example classes and via blackboard's gradecentre.<br />
Specific issues and questions are answered throughout the module including example classes.<br />
Feedback on formal examinations is given via the web feedback template.<br />
Module Content: Introduction to petroleum reservoirs; the flow variables, medium variables.<br />
Equation Types; Principles of mass conservation.<br />
Single phase flow, Darcy's Law.<br />
Potential Flow.<br />
Permeability tensors and Upscaling. Layered medium and flow.<br />
Well model and radial flow.<br />
Multiphase flow, Darcy's Law.<br />
Buckley Leverett Flow. Oil recovery calculation.<br />
Unstable flow.<br />
Flow on an incline and effects of gravity.<br />
Upscaled Flow models<br />
Convection Diffusion<br />
Oil spill<br />
(Knowledge of MATLAB is assumed)<br />
Intended Learning Outcomes: A knowledge and understanding of:<br />
The basic principles of mass conservation and formulation of single and multiphase conservation laws according to<br />
equation type. Their fundamental solutions. Upscaling while maintaining medium properties. Stable and unstable flow<br />
regimes. Effect of mobility ratio on oil recovery and water breakthrough.<br />
An ability to (thinking skills):<br />
Understand and formulate flow models, boundary conditions and procedures to solve illustrative problems. Appreciate<br />
the coupled form of the general system of equations.<br />
an ability to (practical skills):<br />
Understand and interpret practical implications, limitations of flow model solutions and use of models in simulation.<br />
an ability to (key skills):<br />
Study independently, use library resources. Effectively take notes and manage working time.<br />
Reading List: Dake, L, Fundamentals of Reservoir <strong>Engineering</strong>, Elsevier, 1978.<br />
Bear, J, Dynamics of Fluids in Porus Media, Dover Edition, 1988.<br />
Crichlow, Modern Reservoir <strong>Engineering</strong> - A Simulation Approach, Prentice Hall, 1977.
Additional Notes: Lecture notes provided.<br />
Failure to sit an examination or submit work by the specified date will result in a mark of 0% being recorded.<br />
Assessment: 30% continuous assessment assignments, 70% closed book examination.<br />
Practical Work: Exercises/project given during course